2. THE OBSERVED PROPERTIES OF GALAXY CLUSTERS

Observational studies of galaxy clusters have now developed into a broad, multi-faceted and multi-wavelength field. Before we embark on our overview of different theoretical aspects of cluster formation, we briefly review the main observational properties of clusters and, in particular, the basic properties of their main matter constituents.

Figure 1 shows examples of the multiwavelength observations of two massive clusters at two different cosmic epochs: the Abell 1689 at z = 0.18 and the SPT-CL J2106-5844 at z = 1.133. It illustrates all of the main components of the clusters: the luminous stars in and around galaxies (the intracluster light or ICL), the hot ICM observed via its X-ray emission and the Sunyaev-Zel'dovich effect and, in the case of Abell 1689, even the presence of invisible DM manifesting itself through gravitational lensing of background galaxies distorting their images into extended, cluster-centric arcs (Bartelmann 2010, and references therein). At larger radii, the lensing effect is weaker. Although not easily visible by eye, it can still be reliably measured by averaging the shapes of many background galaxies and comparing the average with the expected value for an isotropic distribution of shapes. The gravitational lensing is a direct probe of the total mass distribution in clusters, which makes it both extremely powerful in its own right and a very useful check of other methods of measuring cluster masses. The figure shows several bright elliptical galaxies that are typically located near the cluster center. A salient feature of such central galaxies is that they show little evidence of ongoing star formation, despite their extremely large masses.

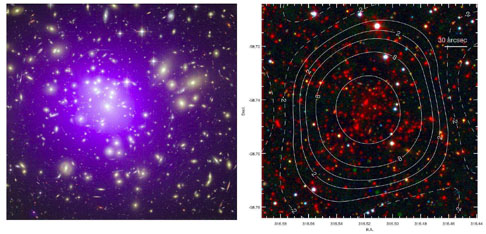Figure 1. Left panel: the composite X-ray/optical image (556 kpc on a side) of the galaxy cluster Abell 1689 at redshift z = 0.18. The purple haze shows X-ray emission of the T ~ 108 K gas, obtained by the Chandra X-ray Observatory. Images of galaxies in the optical band, colored in yellow, are from observations performed with the Hubble Space Telescope. The long arcs in the optical image are caused by the gravitational lensing of background galaxies by matter in the galaxy cluster, the largest system of such arcs ever found (Credit:X-ray: NASA/CXC/MIT; Optical: NASA/STScI). Right panel: the galaxy cluster SPT-CL J2106-5844 at z = 1.133, the most massive cluster known at z > 1 discovered via its Sunyaev-Sel'dovich (SZ) signal (M200 1.3 × 1015 M). The color image shows the Magellan/LDSS3 optical and Spitzer/IRAC mid-infrared measurements (corresponding to the blue-green-red color channels). The frame subtends 4.8 × 4.8 arcmin, which corresponds to 2.4 × 2.4 Mpc at the redshift of the cluster. The white contours correspond to the South Pole Telescope SZ significance values, as labeled, where dashed contours are used for the negative significance values. (Adapted from Foley et al. 2011).

The diffuse plasma is not associated with individual galaxies and constitutes the intra-cluster medium, which contains the bulk of the normal baryonic matter in massive clusters. Although the hot ICM is not directly associated with galaxies, their properties are correlated. For example, Fig. 2 shows the mass of the ICM gas within the radius R₅₀₀, defined as the radius enclosing mean overdensity of _c = 500_cr, versus stellar mass in galaxies within the same radius for a number of local (z 0.1) and distant (0.1 < z < 0.6) clusters (Lin et al. 2012). Here _cr(z) = 3H(z)² / (8 G is the critical mean density of the Universe, defined in terms of the Hubble function H(z). The figure shows a remarkably tight, albeit non-linear, correlation between these two baryonic components. It also shows that the gas mass in clusters is on average about ten times larger than the mass in stars, although this ratio is systematically larger for smaller mass clusters, ranging from M_∗ / M_g 0.2 to 0.05, as mass increases from group scale (M₅₀₀ ~ few × 10¹³ M) to massive clusters (M₅₀₀ ~ 10¹⁵ M).

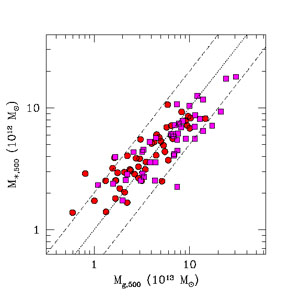Figure 2. The mass in stars vs. the mass of hot, X-ray emitting gas. Both masses are measured within the radius R500 estimated from the observationally calibrated YX - M500 relation, assuming flat CDM cosmology with m = 1 - = 0.26 and h = 0.71. Red circles show local clusters located at z < 0.1, whereas magenta squares show higher-redshift clusters: 0.1 < z < 0.6 (see Lin et al. 2012 for details). The dotted line corresponds to the constant stellar-to-gas mass ratio M∗,500 / Mg,500 = 0.1, whereas the dashed lines correspond to the values of 0.05 and 0.2 for this ratio.

The temperature of the ICM is consistent with velocities of galaxies and indicates that both galaxies and gas are nearly in equilibrium within a common gravitational potential well. The mass of galaxies and hot gas is not sufficient to explain the depth of the potential well, which implies that most of the mass in clusters is in a form of DM. Given that hydrogen is by far the most abundant element in the Universe, most of the plasma particles are electrons and protons, with a smaller number of helium nuclei. There are also trace amounts of heavier nuclei some of which are only partially ionized. The typical average abundance of the heavier elements is about one-third of that found in the Sun or a fraction of one per cent by mass; it decreases with increasing radius and can be quite inhomogeneous, especially in merging systems (Werner et al. 2008, for a review).

Thermodynamic properties of the ICM are of utmost importance, because comparing such properties to predictions of baseline models without cooling and heating can help to isolate the impact of these physical processes in cluster formation. The most popular baseline model is the self-similar model of clusters developed by Kaiser (1986), which we consider in detail in Section 3.9 below. In its simplest version, this model assumes that clusters are scaled versions of each other, so that gas density at a given fraction of the characteristic radius of clusters, defined by their mass, is independent of cluster mass. Figure 3 shows the electron density in clusters as a function of ICM temperature (and hence mass) at different radii. It is clear that density is independent of temperature only outside cluster core at r ~ R₅₀₀, although there is an indication that density is independent of temperature at r = R₂₅₀₀ for k_BT 3 keV. This indicates that processes associated with galaxy formation and feedback affect the properties of clusters at r R₂₅₀₀, but their effects are mild at larger radii.

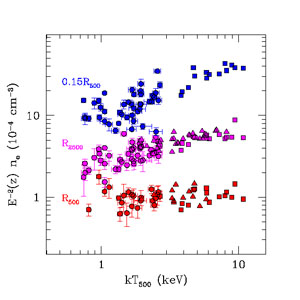Figure 3. The observed electron number density, ne, in galaxy clusters and groups, measured at different radii (from top to bottom: 0.15R500, R2500, R500; see labels) as a function of the intracluster medium temperature at R500. The values of ne are rescaled by E-2(z), the scaling expected from the definition of the radii at which densities are measured. Squares and circles show systems observed with the Chandra X-ray Observatory from the studies by Vikhlinin et al. (2009a) and Sun et al. (2009), triangles show systems observed with the XMM-Newton telescope by Pratt et al. (2010). Note that electron densities at large radii are independent of temperature, as expected from the self-similar model, whereas at small radii the rescaled densities increase with temperature. Note also that the scatter from cluster to cluster increases with decreasing radius, especially for low-temperature groups (after Sun 2012).

During the past two decades, it has been established that the core regions of the relaxed clusters are generally characterized by a strongly peaked X-ray emissivity, indicating efficient cooling of the gas (e.g., Fabian 1994). Quite interestingly, spectroscopic observations with the Chandra and XMM-Newton satellites have demonstrated that, despite strong X-ray emission of the hot gas, only a relatively modest amount of this gas cools down to low temperatures (e.g., Peterson et al. 2001, Böhringer et al. 2001). This result is generally consistent with the low levels of star formation observed in the brightest cluster galaxies (BCGs; e.g., McDonald et al. 2011). It implies that a heating mechanism should compensate for radiative losses, thereby preventing the gas in cluster cores to cool down to low temperature. The presence of cool cores is also reflected in the observed temperature profiles (e.g. Leccardi & Molendi 2008, Pratt et al. 2007, Vikhlinin et al. 2006, see also Figure 4), which exhibit decline of temperature with decreasing radius in the innermost regions of relaxed cool-core clusters.

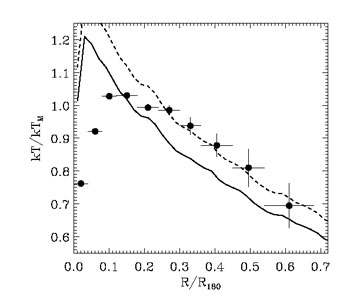Figure 4. Comparison between temperature profiles, normalized to the global temperature measured within R180 by Leccardi & Molendi (2008), for a set of about 50 nearby clusters with z 0.3 and with temperature kBTX > 3 keV, observed with the XMM-Newton (dots with errorbars) and results from cosmological hydrodynamical simulations including the effect of radiative cooling, star formation and supernova feedback in the form of galactic winds (solid curve; Borgani et al. 2004). From Leccardi & Molendi (2008).

One of the most important and most widely studied aspects of ICM properties are correlations between its different observable integrated quantities and between observable quantities and total mass. Such scaling relations are the key ingredient in cosmological uses of clusters, where it is particularly desirable that the relations are characterized by small scatter and are independent of the relaxation state and other properties of clusters. Although clusters are fascinatingly complex systems overall, they do exhibit some remarkable regularities. As an example, Figure 5 shows the correlation between the bolometric luminosity emitted from within R₅₀₀ and the Y_X parameter defined as a product of gas mass within R₅₀₀ and ICM temperature derived from the X-ray spectrum within the radial range (0.15 - 1)R₅₀₀ (Kravtsov, Vikhlinin & Nagai 2006) for the Representative XMM-Newton Cluster Structure Survey (REXCESS) sample of clusters studied by Pratt et al. (2009). Different symbols indicate clusters in different states of relaxation, whereas clusters with strongly peaked central gas distribution (the cool core clusters) and clusters with less centrally concentrated gas distribution are shown with different colors. The left panel shows total luminosity integrated within radius R₅₀₀, wheareas the right panel shows luminosity calculated with the central region within 0.15R₅₀₀ excised. Quite clearly, the core-excised X-ray luminosity exhibits remarkably tight correlation with Y_X, which, in turn, is expected to correlate tightly with total cluster mass (Kravtsov, Vikhlinin & Nagai 2006, Stanek et al. 2010, Fabjan et al. 2011). This figure illustrates the general findings in the past decade that clusters exhibit strong regularity and tight correlations among X-ray observable quantities and total mass, provided that relevant quantities are measured after excluding the emission from cluster cores.

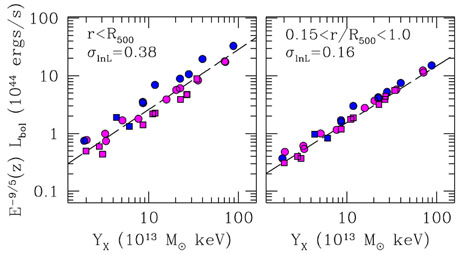Figure 5. Correlation of bolometric luminosity of intracluster gas and YX Mgas TX, where Mgas is the mass of the gas within R500 and TX is temperature derived from the fit to gas spectrum accounting only for emission from radial range (0.15 - 1)R500. Results are shown for the local clusters from the Representative XMM-Newton Cluster Structure Survey sample of Pratt et al. (2009). The left panel shows total luminosity integrated within radius R500, whereas the right panel shows bolometric luminosity calculated with the central 0.15R500 of the cluster excised. Labels in the top left corner indicate the radial range used in computing the luminosity and logarithmic scatter of luminosity at fixed YX. The blue points show cool core clusters, whereas magenta points are non-cool core clusters. Clusters classified as relaxed and disturbed are shown by circles and squares, respectively. Note that exclusion of the cluster cores reduces the scatter between luminosity and YX by more than a factor of two.