5. CLUSTER FORMATION IN ALTERNATIVE COSMOLOGICAL MODELS

In previous sections, we have discussed the main elements of cluster formation in the standard CDM cosmology. Although this model is very successful in explaining a wide variety of observations, some of its key assumptions and ingredients are not yet fully tested. This provides motivation to explore different assumptions and alternative models.

As discussed in Section 3.7, the halo mass function for a Gaussian random field is uniquely specified by the peak height = _c / (R, z), where R is the filtering scale corresponding to the cluster mass scale M. For sufficiently large mass, that is rare peaks with ≫ 1, the mass function becomes exponentially sensitive to the value of . At the same time, the mass function also determines the halo bias (see Section 3.8). Again, for ≫ 1 and Gaussian perturbations, the bias function scales as b() ~ ² / _c = / (R, z). Therefore, the cluster 2-point correlation function can be written as _cl(r) = ²(_R(r) / _R²), where _R(r) is the correlation function of the smoothed fluctuation field (see Section 3.1). Once the peak height is constrained by requiring a model to predict the observed cluster abundance, the value of the cluster correlation function at a single scale r provides a measurement of the shape of the power spectrum through the ratio of the clustering strength at the scale r and at the cluster characteristic scale R. These predictions are only valid under two assumptions, namely Gaussianity of primordial density perturbations and scale independence of the linear growth function D(z), as predicted by the standard theory of gravity. Therefore, the combination of number counts and large-scale clustering studies offers a powerful means to constrain the possible violation of either one of these two assumptions that hold for the CDM model.

In this section, we briefly review the specifics of cluster formation in models with non-Gaussian initial density field and with non-standard gravity, the most frequently discussed modifications to the standard structure formation paradigm.

5.1. Mass function and bias of clusters in non-Gaussian models

One of the key assumptions of the standard model of structure formation is that initial density perturbations are described by a Gaussian random field (see Section 3.1). The simplest single-field, slow-roll inflation models predict nearly Gaussian initial density fields. However, deviations from Gaussianity are expected in a broad range of inflation models that violate slow-roll approximation, and have multiple fields, or modified kinetic terms (see Bartolo et al. 2004 for a review). Given that there is no single preferred inflation model, we do not know which specific form of non-Gaussianity is possibly realized in nature. Deviations from Gaussianity are parameterized using a heuristic functional form. One of the simplest and most common choices for such a form is the local non-Gaussian potential given by 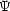_NG(x) = -(_g(x) + f_NL[_g(x)² - <_g²>]), where 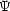_NG is the usual Newtonian potential, _g is the Gaussian random field with zero mean, and the parameter f_NL = const controls the degree and nature of non-Gaussianity (e.g., Salopek & Bond 1990, Matarrese, Verde & Jimenez 2000, Komatsu & Spergel 2001). The simplest inflation models predict f_NL 10^-2 (e.g., Maldacena 2003), but a number of models that predict much larger degree of non-Gaussianity exist as well (Bartolo et al. 2004). The current CMB constraint on scale-independent non-Gaussianity is f_NL = 30 ± 20 at the 68% confidence level (e.g., Komatsu 2010) and there is thus still room for existence of sizable deviations from Gaussianity.

The non-Gaussian fields with f_NL < 0 have a PDF of the potential field that is skewed toward positive values and the abundance of peaks that seed the collapse of halos is reduced compared to Gaussian initial conditions. Conversely, the PDF of the potential field in models with f_NL > 0 has negative skewness, and hence an increased number of potential minima (density peaks). This would result in an enhanced abundance of rare objects, such as massive distant clusters, relative to the Gaussian case (see, e.g., figure 1 in Dalal et al. 2008 for an illustration of the effect of f_NL on the large-scale structure that forms). The suppression or enhancement of abundance of halos increases with increasing peak height.

The mass functions resulting from non-Gaussian initial conditions have been studied both analytically (e.g., Chiu, Ostriker & Strauss 1998, Matarrese, Verde & Jimenez 2000, Lo Verde et al. 2008, Afshordi & Tolley 2008) and using cosmological simulations (Grossi et al. 2007, Dalal et al. 2008, Lo Verde et al. 2008, LoVerde & Smith 2011, Wagner & Verde 2012). These studies showed that accurate formulae for the halo abundance from the initial linear density field exist for the non-Gaussian models as well. The general result is that the fractional change in the abundance of the rarest peaks is of order unity for the initial fields with |f_NL| ~ 100. The abundance of clusters is thus only mildly sensitive to deviations of Gaussianity within the currently constrained limits (Scoccimarro, Sefusatti & Zaldarriaga 2004, Sefusatti et al. 2007, Sartoris et al. 2010, Cunha, Huterer & Doré 2010). In contrast, primordial non-Gaussianity may also leave an imprint in the spatial distribution of clusters in the form of a scale-dependence of large-scale linear bias.

As was discovered by Dalal et al. (2008) and confirmed in subsequent analytical (Matarrese & Verde 2008, McDonald 2008, Afshordi & Tolley 2008, Taruya, Koyama & Matsubara 2008, Slosar et al. 2008) and numerical studies (Desjacques, Seljak & Iliev 2009, Pillepich, Porciani & Hahn 2010, Grossi et al. 2009, Shandera, Dalal & Huterer 2011), the linear bias of collapsed objects in the models with local non-Gaussianity can be described as a function of wavenumber k by b_NG = b_g + f_NL × const / k², where b_g is the linear bias in the corresponding cosmological model with the Gaussian initial conditions discussed in Section 3.8. This scale dependence arises because in the non-Gaussian models the large-scale modes that boost the abundance of peaks are correlated with the peaks themselves, which enhances (or suppresses) the peak amplitudes by a factor proportional to f_NL f_NL / k². Because this effect of modulation increases with increasing peak height, = _c / (M, z), the scale-dependence of bias increases with increasing halo mass. This unique signature can be used as a powerful constraint on deviations from Gaussianity (at least for models with local non-Gaussianity) in large samples of clusters in which the power spectrum or correlation function can be measured on large scales.

5.2. Formation of clusters in modified gravity models

Recently, there has been a renewed interest in modifications to the standard GR theory of gravity (e.g., see Capozziello & de Laurentis 2011, Durrer & Maartens 2008, Silvestri & Trodden 2009) for recent reviews). These models have implications not only for cosmic expansion, but also for the evolution of density perturbations and, therefore, for the formation of galaxy clusters.

For instance, in the class of the f(R) models, cosmic acceleration arises from a modification of gravity law given by the addition of a general function f(R) of the Ricci curvature scalar R in the Einstein-Hilbert action (see, e.g., Sotiriou & Faraoni 2010, Jain & Khoury 2010 for recent reviews). Such modifications result in enhancements of gravitational forces on scales relevant for structure formation in such a way that the resulting linear perturbation growth rate D becomes scale dependent; whereas on very large scales gravity behaves similarly to GR gravity, on smaller scales it is enhanced compared to GR and the rate of structure formation is thereby also enhanced. The nonlinear halo collapse and growth are also faster in f(R) models, which leads to enhanced abundance of massive clusters (Schmidt et al. 2009, Ferraro, Schmidt & Hu 2011, Zhao, Li & Koyama 2011) compared to the predictions of the models with GR gravity and identical cosmological parameters. Likewise, the peaks collapsing by a given z have lower peak height in the modified gravity models compared to the peak height in the standard gravity model. This results in the reduced bias of clusters of a given mass compared to the standard model. Furthermore, the scale dependence of the linear growth also induces a scale dependence of bias, thus offering another route to detect modifications of gravity (Parfrey, Hui & Sheth 2011). Qualitatively similar effects on cluster abundance and bias are expected in the braneworld-modified gravity models based on higher dimensions, such as the Dvali-Gabadadze-Porrati (DGP, Dvali, Gabadadze & Porrati 2000) gravity model (Schäfer & Koyama 2008, Khoury & Wyman 2009, Schmidt 2009, Schmidt, Hu & Lima 2010) and its successors with similar LSS phenomenology consistent with current observational constraints, such as models of ghost-free massive gravity (de Rham, Gabadadze & Tolley 2011, D'Amico et al. 2011).

A general consequence of modifying gravity is that the Birkhoff theorem no longer holds, which does not allow a straightforward extension of the spherical collapse model described in Section 3.2 to a generic model of modified gravity. Nevertheless, numerical calculations of spherical collapse have been presented for a number of specific models (e.g., Schäfer & Koyama 2008, Schmidt et al. 2009, Schmidt, Hu & Lima 2010, Martino, Stabenau & Sheth 2009). For both the f(R) and the DGP classes of models, the results of simulations obtained so far suggest that halo mass function and bias can still be described by the universal functions of peak height, in which the threshold for collapse and the linear growth rate are modified appropriately from their standard model values (Schmidt et al. 2009, Schmidt, Hu & Lima 2010). This implies that it should be possible to calibrate mass function and bias of halos in the modified gravity models with the accuracy comparable to that in the standard structure formation models.