1.5. THE USE OF SCALING RELATIONS

Rather than studying individual galaxies one can also study them by investigating the evolution of so-called scaling relations. Nearby galaxies happen to display clear correlations between well-defined and easily measurable galaxy properties. With high redshift studies now routine, scaling relations are more useful than ever, allowing us to probe the evolution of galaxy populations over a large range of lookback times (e.g. Bell et al. 2004, Saglia et al. 2010). In this review I will discuss the color - (and line strength -) relation, a potentially tight relation connecting the galaxy mass to its stellar populations, and the fundamental plane of galaxies, a relation connecting the structure of galaxies to their mass.

1.5.1. The color - relation

It has been known now for more than 50 years that early-type galaxies show a tight color-magnitude (C-M) relation (Baum 1959, Sandage 1972; Visvanathan & Sandage 1977), in the sense that larger galaxies are redder. Bower et al. (1992) showed that in the Virgo and Coma clusters, when taking small central apertures, the scatter in U-V, and V-K is extremely small. Noting that when galaxies age, their color becomes redder, and their velocity dispersion only changes slightly, they could show that cluster ellipticals are made of very old stars, with the bulk of them having formed at z > 2. so, by assuming that for a given the eldest galaxies are situated at the reddest color, and that along the color - relation the metallicity (and possibly also the maximum age for galaxies of a certain ) changes, one can derive relative ages and metallicities using color - relations. It has been used as an important benchmark for theories of galaxy formation and evolution (e.g. Bell et al. 2004; Bernardi et al. 2005) Galaxies devoid of star formation are thought to populate the red sequence, while star-forming galaxies lie in the blue cloud (e.g. Baldry et al. 2004). The dichotomy in the distribution of galaxies in this relation has opened a very productive avenue of research to unravel the epoch of galaxy assembly (e.g. De Lucia et al. 2004; Andreon 2006; Arnouts et al. 2007).

This stellar population - mass relation for galaxies has manifested itself in the literature in many flavors. Various colors have been used, from blue colors that are very age-sensitive to red colors covering a large wavelength baseline (e.g. V-K). To avoid the effects of dust extinction, one often uses line strengths instead of colors. The Mg₂ - relation has been used very frequently in the literature (e.g. Terlevich et al. 1981). SDSS related studies have been concentrating on the H line and the D₄₀₀₀ break (Kauffmann et al. 2003), finding that galaxies less massive that 3 × 10¹⁰ M are predominantly younger than more massive galaxies. Cenarro et al. (2003) find an inverse relation of the Ca II IR triplet strength as a function of , which up to recently is not well understood, and might have something to do with IMF-changes in galaxies (see Section 1.4.6). The galaxy mass indicator (i.e., here ) can be replaced by other indicators such as galaxy luminosity, stellar mass, etc. When using stellar mass, the relations are not so tight (e.g. Peletier et al. 2012), since compact ellipticals fall off the relation for the other galaxies. Compact ellipticals have higher and also redder colors/line indices than one would expect from their stellar mass. What helps in any case is taking into account both random () and regular motion (rotation) (Zaritsky et al. 2006). This way both ellipticals and spiral galaxies can be compared easily with each other (Falcón-Barroso et al. 2011). An advantage is that the color - relation is independent of galaxy distance. When using mass, or luminosity, the errors involved in measuring these distances will generally dominate the scatter, unless these errors can be avoided, in e.g. a galaxy cluster.

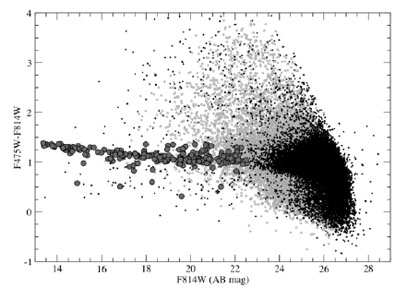
In Fig. 1.23 I show two color - magnitude relations in the Coma cluster. On the right is shown the result of Bower et al. (1999), showing spectroscopically confirmed cluster members. One sees that ellipticals and S0s form a tight color - magnitude relation. Spiral galaxies are bluer for a given magnitude, indicating younger ages. At fainter magnitudes more and more galaxies are falling blue-ward of the relation, showing that star formation in smaller galaxies is more common. On the left, a diagram is shown from the Coma-ACS survey (Hammer et al. 2010) a survey at a much higher resolution of a small part of the Coma cluster. Many dwarfs are included. At faint magnitudes, many galaxy are shown to be redder or bluer than the linear relation. These are mostly background galaxies, shown by the fact that the larger symbols, the spectroscopically confirmed Coma cluster members, almost all lie on or below the relation. A few compact ellipticals in Coma lie above the relation.

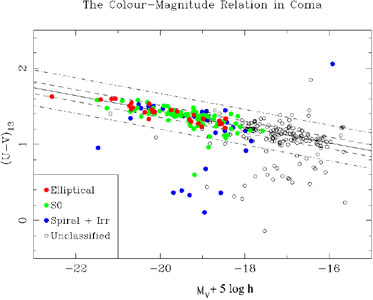Figure 1.23. The color - magnitude relation in the Coma cluster. Top: F475W - F814W vs. F814W relation from the Coma-ACS survey (Hammmer et al. 2010). These apparent magnitudes can be converted to absolute magnitudes using m-M = 35. Bottom: U-V vs. MV relation from Bower et al. (1999).

Also for spiral galaxies, the color - relation can be used very well to study stellar populations. Falcón-Barroso et al. (2002) showed that bulges with old stellar populations fall on the tight Mg b - relation for elliptical galaxies and S0's. This means that the stellar populations in the bulge of a galaxy is not determined by the mass of the whole galaxy, but by the mass (or ) of the bulge (similar to the black hole mass - Ferrarese & Merritt 2000). So, by plotting an index, such as Mg b against central , one can use the relation in the same way as for ellipticals. In Fig. 1.24 this is done for the spirals of the SAURON survey (Peletier et al. 2007, Ganda et al. 2007). Plotted are central line strengths. The figure shows that the central stellar populations in late-type spirals are all younger than the ones in early-type galaxies. Sa's show a large scatter, and have luminosity-weighted stellar populations that range from very young to as old as ellipticals. The diagram on the right, which uses H (in magnitudes) is maybe a better diagram to use, since here the dependence of the index on is much lower, which means that one can read off ages much more easily. The H - diagram has not been used very often in the literature, since only recently one is able to clean the absorption from the H emission. The H - diagram shows the same results as Mg b - : much more scatter in the stellar populations in Sa's (and some small E's and S0's) than in later type galaxies, which, on the other hand, are younger than ellipticals.

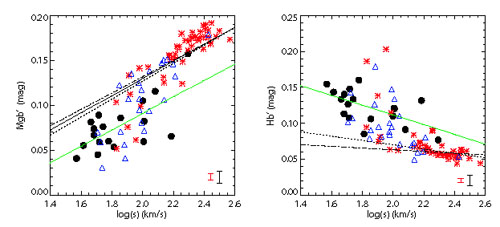Figure 1.24. Mg b - and H - relations for 90 ellipticals and bulges from the SAURON sample (from Ganda et al. 2007). Elliptical galaxies are indicated with red asterisks, Sa's with blue open triangles, and later type spirals with filled black circles.

1.5.2. Stellar Population Analysis from Spitzer Colors

In recent years the Spitzer Space Telescope has made many observations in 4 bands. The shortest wavelength bands, [3.6] and [4.5], in nearby galaxies are mainly dominated by stellar light, while the [8.0] bands mainly detects warm dust from particles like PAHs (Fazio et al. 2004). Since the light at 3.6 and 4.5 µm is barely affected by extinction, and also not by young, hot stars, the [3.6] - [4.5] color seems to be useful to study the cold stars in early-type galaxies. The color will be affected by AGN and TP-AGB stars, and will also be dependent on metallicity. In Fig. 1.25 predictions are shown for the [3.6] - [4.5] color from Marigo et al. (2008) and Charlot & Bruzual (Version of 2007, unpublished) for SSPs of various ages and metallicity. Note that in both sets of models stellar populations of ~ 1 Gyr make this color particularly red ([3.6] - [4.5] goes to larger values). The models do not agree with each other in predicting the dependence of [3.6] - [4.5] as a function of metallicity for old ages: in the Marigo (2008) models [3.6] - [4.5] becomes bluer with increasing metallicity, while in Charlot & Bruzual the colors becomes redder.

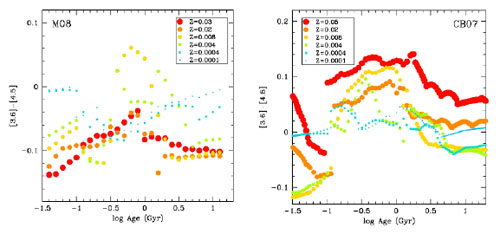Figure 1.25. SSP Models for [3.6] - [4.5] by Marigo et al. (2008, left) and Charlot & Bruzual (Version of 2007, unpublished) as a function of age and metallicity.

In Peletier et al. (2012) we describe a study of the [3.6] - [4.5] color in the 48 early-type galaxies of the SAURON sample. It is shown that the images in the 2 bands look like smooth, elliptical galaxies in the optical, without dust lanes etc. For every object colors were determined in circular apertures of r_e and r_e / 8. Also radial color profiles were determined by 1. Convolving the 3.6 µm image with the 4.5 µm PSF and vice-versa, to remove any PSF-effects near the center; 2. Fitting the same ellipses, with fixed center, ellipticity and position angle in both bands; 3. Performing accurate sky subtraction; and 4. Making the ratio of both profiles. One color profile is shown in Fig. 1.26, where we show the (optical) SAURON continuum image, the H absorption map, and the [3.6] - [4.5] color profile. The high values in the H map show the stellar populations in the dust lane, which are younger than in the main galaxy. The [3.6] - [4.5] profile shows that these young stellar populations make the color redder. On top of that, the general gradient is making the galaxy slowly redder when going outwards. Given the fact that most galaxies become less metal rich going outward, this might mean that [3.6] - [4.5] becomes redder for decreasing metallicity, or bluer for increasing metallicity. We can understand this when we know that the 4.5 µm band contains a large CO absorption band. When the metallicity increases, this band gets stronger, making [3.6] - [4.5] bluer (see Peletier et al. 2012).

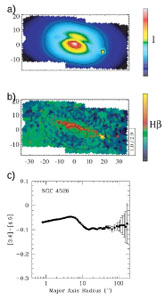Figure 1.26. SAURON images in V-band continuum (a)) and H absorption for NGC 4526. The yellow spot is a foreground star. In the bottom panel is shown the [3.6] - [4.5] profile. The central redder part of the profile corresponds exactly to the inner disk seen in the upper 2 panels (from Peletier et al. 2012).

Most galaxies have colors everywhere between -0.15 and 0. An exception is M87, the central Virgo galaxy, which has a very red center, due to the synchrotron emission in center and jet. No other galaxies contain such prominent central point sources. When plotting the relation of [3.6] - [4.5] and (Fig. 1.27) we see that both quantities are strongly related. In this diagram we have colored the galaxies with their age inside r_e / 8, as obtained by Kuntschner et al. (2010) from the SAURON line indices. Had we used ages within r_e, the figure would have been similar, but with a smaller range in colors. This is because in these early-type galaxies many more young features are seen in the inner parts than further out. The color - relation shows that more massive galaxies are bluer. The color coding of the figure shows that these galaxies are at the same time older, if one considers the luminosity-weighted SSP-ages. The main difference with other colors is that the [3.6] - [4.5] color becomes bluer for increasing galaxy mass/luminosity.

Figure 1.27. [3.6] - [4.5] color as a function of velocity dispersion in km/s. The velocity dispersion has been measured within re. Here the color, determined within 1 effective radius, is shown.

So, what is the origin of this color - relation? Here one has to use mainly empirical arguments, since the models still are rather uncertain. One could think that metallicity is the main driver, with galaxies becoming less metal rich for decreasing , and as a result redder. On the other hand, one does not know what the metallicity dependence of [3.6] - [4.5] is. One could also think that age is the dominant driver. In this case the fraction of AGB stars has to increase with decreasing . Since these stars are red, the galaxy colors then become redder. If this proves to be true, this would be a promising way to determine the contribution from AGB stars in galaxies. If the scatter in the color - relation can be explained by young stellar populations on top of a much older underlying stellar population, one would expect the outliers of the optical line strength - relations of Kuntschner et al. (2006) to be the same as the outliers of the color - relation here. A close look teaches us that this is to first order the case. Also, there is a strong correlation between Mg b and [3.6] - [4.5]. If the color - relation is driven by age, it would mean that the young populations that are responsible for the bluing of [3.6] - [4.5] are also responsible both for the decreasing Mg b and increasing H index. Although it is hard to quantify what kind of SSP would be needed, the strong correlation between Mg b, which is sensitive for stellar populations from 10^6-7 y, and [3.6] - [4.5], which is mostly sensitive to stars above 3 × 10⁸ y, would indicate that stellar populations in these galaxies would have ages older than 3 × 10⁸ y. This is not very realistic, since the galaxies that are blue in the [3.6] - [4.5] - relation always show H emission lines in the region of the young stars, indicating recent star formation. The alternative would be that AGB-populations are much less important than people think. That would agree with recent results from Zibetti et al. (2012), who, from near-infrared spectroscopy of post-starburst galaxies, find a much lower contribution from AGB stars than is expected from the TP-AGB heavy models of Maraston (2005). More research clearly is needed to understand the contribution of this evolved stellar population in galaxies.

1.5.3. The fundamental plane of galaxies

Since its discovery (Djorgovski & Davis 1987; Dressler et al. 1987), the Fundamental Plane (FP) has been one of the most studied relations in the literature. Given its tightness, like many other scaling relations the FP was quickly envisaged as a distance estimator as well as a correlation to understand how galaxies form and evolve (e.g. Bender, Burstein & Faber 1992 (BBF), Jørgensen et al. 1996; Pahre et al. 1998; Bernardi et al. 2003). It is widely recognized that the FP is a manifestation of the virial theorem for self-gravitating systems averaged over space and time with physical quantities total mass, velocity dispersion, and gravitational radius replaced by the observables mean effective surface brightness µ_e, effective (half-light) radius (r_e), and stellar velocity dispersion . Since velocity dispersion and surface brightness are distance-independent quantities, contrary to effective radius, it is common to express the FP as log(r_e) = log() + µ_e + , to separate distance-errors from others. If galaxies were homologous with constant total mass-to-light ratios, the FP would be equivalent to the virial plane and be infinitely thin, with slopes = 2 and = 0.4. By studying the intrinsic scatter around the FP, one can study how galaxy properties differ within the observed sample.

Just like the color - relation, the FP is a very useful tool to study the evolution of stellar populations. To first order approximation, radius and are independent of stellar populations, while µ_e is. If a stellar population ages, its luminosity decreases, and therefore also its surface brightness. However, if one studies the evolution with redshift, one also has to take into account the fact that galaxies become more compact with redshift (radius evolution), and consequently their velocity dispersion increases as well.

An important study to mention here is the EDisCS study of the FP of galaxies in clusters up to z = 0.9 (Saglia et al. 2010). Combining structural parameters from HST and VLT images and velocity dispersions from VLT spectra, they have been able to determine Fundamental Plane fits for clusters with a range in redshift, as well as for galaxies in the field. At face-value, on average, the evolution of the surface brightness follows the predictions of simple stellar population models with high formation redshift (~ z = 2) for all clusters, independent of their total mass (see Fig. 1.28). However, it looks as if both the evolution of early-type galaxies with redshift and the dependence of this evolution on environment differ for galaxies of different mass. These differences manifest themselves as an evolution in the FP coefficient as a function of redshift. They also find size and velocity dispersion evolution of the sample. However, after taking into account the progenitor bias affecting the sample (large galaxies that joined the local early-type class only recently will progressively disappear in higher redshift samples), the effective size and velocity dispersion evolution reduce substantially. So after making corrections for radius and velocity dispersion evolution, they found, using SSP models, that massive (M > 10¹¹ M) cluster galaxies are old, with formation redshifts z > 1.5. In contrast, lower mass galaxies are just 2 to 3 Gyr old. This agrees with the EDisCS results from colors and line strength (e.g. Poggianti et al. 2006) who argue that the lower luminosity, lower mass population of early-type galaxies comes in place only at later stages in clusters. Field galaxies follow the same trend, but are ~ 1 Gyr younger at a given redshift and mass. This picture in principle is in agreement with the picture one gets from stellar population analysis of nearby galaxies (Thomas et al. 2005).

Figure 1.28. Redshift evolution of the B band mass-to-light ratio (from Saglia et al. 2010). The full black lines show the simple stellar population (SSP) predictions for a Salpeter IMF and formation redshift of either zf = 2(lower) or 2.5 (upper curve) and solar metallicity from Maraston (2005). The blue line shows the SSP for zf = 1.5 and twice-solar metallicity, the magenta line the SSP for zf = 2.5 and half-solar metallicity. The dotted line shows the best-fit linear relation and the errors dashed.

In the local Universe, the high S/N of the observations make it possible to look at the FP in more detail. Here we can study the position of bulges on the FP (e.g. Bender et al. 1992, Falcón-Barroso et al. 2002), the scatter in the stellar population ages of galaxies, the amount of dark matter in various types of galaxies along the FP, etc. Falcón-Barroso et al. (2011) (Fig. 1.29) studied the FP for the SAURON sample of 48 E/S0 galaxies and 24 Sa's. To avoid the effects of internal extinction in galaxies, they use the Spitzer 3.6 µm band. The velocity dispersion they use is the dispersion calculated using the integrated spectrum inside 1 effective radius. If measured in this way, it includes both rotation and random motions (Zaritsky et al. 2006), and both ellipticals and spirals can be put on the same diagram. Falcón-Barroso et al. find that the SAURON slow rotators (SR, Emsellem et al. 2007) define a very tight FP, tighter than the fast rotators. This confirms the study from colors and line indices that SR are uniformly old systems, although it also shows that slow rotators have the same homology (radius - surface brightness - mass relations). In the V-band the spiral galaxies deviate because of younger stellar populations, but also because of extinction, two effects which work in opposite directions.

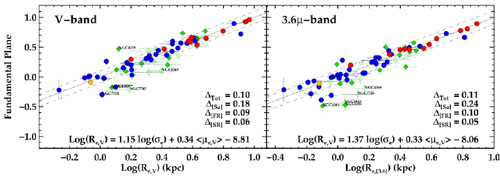Figure 1.29. Edge-on views of the Fundamental Plane relation for the galaxies in the SAURON sample of galaxies in V - and 3.6µm-bands. Circles denote E/S0 galaxies, diamonds Sa galaxies. Filled symbols indicate galaxies with good distance estimates, open symbols those with only recession velocity determinations. In blue we highlight Fast Rotators, in red Slow Rotators and in green the Sa galaxies. The special case of NGC 4550, with two similarly-massive counter-rotating disc-like components, is marked in yellow. The solid line is the best fit relation (as indicated in the equation in each panel) (from Falcón-Barroso et al. 2011).

If one goes down in mass towards dwarf galaxies, one traditionally finds that dwarf ellipticals lie above the fundamental plane (BBF, de Rijcke et al. 2005). Converting the FP-parameters into new parameters ₁, ₂ and ₃ using a coordinate transformation (from BBF), one can directly see how the mass ( ₁) and M/L ( ₃) evolve. If one does this, one finds that dwarf ellipticals have higher M/L ratios than ellipticals and S0's on the fundamental plane. This result has been revised recently using Toloba et al. (2012), who obtained high quality data for a larger sample of dwarfs (some supported by rotation and some by random motions). From their long-slit data they simulated the integrated spectrum inside an effective radius, to determine the generalized dispersion (Zaritsky et al. 2006) also for the dwarfs. They show that also the new data for dwarf galaxies fall above the fundamental plane. Correcting for the effects of stellar populations using line indices from Michielsen et al. (2008) in the way described by Graves & Faber (2010) they find that the objects remain above the FP, and have dynamical to stellar mass ratios around 1.5 (see Fig. 1.30). If one, however, goes down to even lower mass dwarfs, these ratios rise to much higher values (Wolf et al. 2010).

Figure 1.30. The position of dwarf ellipticals on FP (from Toloba et al. 2012). The early-type galaxies and Sa's are from Falcón-Barroso et al. 2011. Shown in red are rotationally supported dwarfs, and in blue pressure supported ones. Note that the dwarfs lie predominantly above the large galaxies, showing intrinsically higher dark matter fractions.