8.3. STAR FORMATION IN GALAXIES - TWO MODES

8.3.1. Quiescent or normal mode of star formation

As discussed in Section 8.1, the star-forming GMCs are self-gravitating with internal velocity dispersions implying an effective internal turbulent pressure typically 100 times the external diffuse ISM pressures. One's physical intuition should then suggest that disturbances in the external, diffuse ISM will have little influence in general on the rate of formation of stars within GMCs. With this in mind, one might expect that normally SFRs will simply depend linearly on the overall mass of H₂ and/or the internal density of the cloud and this logic should hold in other galaxies as long as the GMC properties are roughly similar. Galaxy type or the location within a galaxy should have little influence on what happens within the self-gravitating clouds.

Observations of CO emission (tracing the mass of GMCs) and star formation tracers (FIR luminosity or H) have generally shown a linear proportionality between SFR and H₂ mass distributions. For example, the overall Galactic Hii region radial distribution shown in Fig. 8.2 is similar to that of H₂ as traced by CO. On the scale of individual star-forming clouds, one might expect sizable fluctuations in the SFR per unit mass since the overall Galactic star formation efficiency (SFE) is low with a characteristic star formation timescale ~ 10⁹ yr, i.e., much longer than the GMC internal dynamical timescale ~ 10⁷ yr. In addition, the GMCs may have somewhat variable mean densities which of course alters their internal dynamical timescale. For a sample of individual Galactic GMCs (including ones with and without associated Hii regions), Fig. 8.18 (left panel) shows an approximately `linear' correlation between molecular gas mass M_virial and L_IR or the SFR (Scoville & Good 1989) for GMCs with masses 10⁴ to over 10⁶ M. The scatter off this relation is a factor ~ 4. There is also a clear trend for the most massive clouds which all have Hii regions, presumably in the spiral arms, to have elevated ratios.

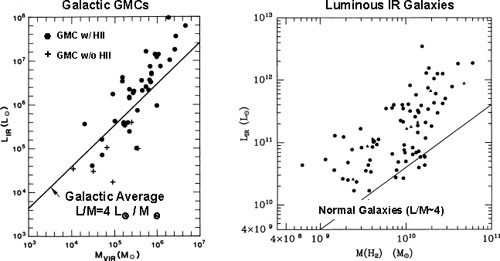Figure 8.18. Left panel: the relation between IR luminosity and H2 mass is shown for a large sample of Galactic GMCs with (dots) and without Hii regions (crosses), compared with the overall Galactic average obtained from dividing the total Milky Way IR luminosity by the total H2 mass (Scoville & Good 1989). M 51 and many other nearby spiral galaxies have mean ratios similar to that of the Milky Way. The right panel shows a similar plot for a local sample of IR bright galaxies (Sanders et al. 1991). The ULIRGs at LIR > 1012 L show much higher luminosity-to-mass ratios, indicating that they are converting gas to stars 10-20 times faster.

In summary, there is good basis (empirical from the observations and theoretical intuition from what we know regarding the GMC structures) for an approximately linear mode of star formation. From local galaxies such as the Milky Way and M 51, this is quantified at 1 M per year per 10⁹ M of H₂, or

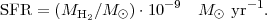(29)

8.3.2. Dynamically-driven starburst mode

At the same time, there are clearly instances, such as those of the IR-bright galaxies, galaxy nuclei and the spirals arms and bars of normal galaxies, where the SFE is significantly enhanced to a level such that they can be classified as starbursts. Figure 8.18 (right panel) shows a plot of the IR luminosities and molecular gas masses for IR-luminous galaxies (LIRGs, Sanders et al. 1991) - all of them have considerably elevated luminosity-to-mass ratios compared to the average ratios for the Milky Way and nearby spiral galaxies like M 51. Both the luminous IR galaxies and the individual spiral arm GMCs have exceptionally high rates of massive star formation (presumably they are also forming low-mass stars). In such regions, the SFE (based on the ratio of L_IR / M_H2) may be enhanced by a factor ten compared to that in Equation 8.29.

In both the spiral arms and the ULIRGs, this elevated SFE appears correlated with non-circular galactic dynamics and high concentrations of dense gas. Galaxy merging leads to dissipative deposition of gas to the centres of the merging systems and spiral arm streaming motions cause crowding of the GMC galactic orbits. As a result of the non-circular motions and concentration of gas clouds, cloud-cloud collisions will be more frequent. If such collisions occur at relative velocity greater than the GMC internal velocities (few km/s), the collisions can compress the internal gas mass and significantly elevate the SFE (Scoville & Hersh 1979; Tan 2000). This high-SFE mode might therefore be referred to as a dynamically-driven starburst where the SFE is 10-50 times that given in Equation 8.29 - occurring in galaxy mergers or localised regions such as spiral arms and nuclear bars of normal galaxy disks.

8.3.3. Star formation `laws'

Over the years a number of prescriptions have been proposed to describe the rates of star formation within galaxies. Early on, Scoville & Good (1989) and Young & Scoville (1991) advocated that the SFR varied linearly with the mass of molecular gas - based on observations of Galactic GMCs and the similarity of molecular gas radial distributions in nearby, normal galaxies to the radial distributions of SFR tracers (e.g., blue light, H and FIR). Extensive studies (Kennicutt 1998) which included Hi in the analysis then led to the well-known Kennicutt-Schmidt SFR law with SFR _HI+H2^1.4 and a threshold cutoff surface density below which the SFR decreased more steeply. In my opinion, the atomic gas (Hi) exhibits almost no correlation with the SFR tracers (recently shown clearly by Bigiel et al. 2008 and Schruba et al. 2011) and is not directly relevant to the star formation process in the inner parts of spiral galaxies. (The non-integral, ~ 1.4, dependence of the SFR in the Kennicutt-Schmidt star formation law is likely due to including Hi in the analysis and is without a direct physical link to star formation except via the formation of molecular clouds and due to the inclusion of starburst galaxy nuclei. As emphasised above, the GMCs are long-lived and stars form from them at low efficiency, so the fact that the Hi is needed to form molecules does not justify a physical connection to the star formation process.)

The most recent compilations have been done by Bigiel et al. (2011) and Krumholz et al. (2012). The former advocate a simple linear dependence on molecular gas surface density; the latter propose a `volumetric' law 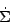_* = f_{H2 ff} / _ff where the factors entering are the H₂ mass fraction, the efficiency of star formation per free-fall time, the total gas surface density and the free-fall time. Their compilation of observational data is shown in Fig. 8.19, together with the various star formation laws they evaluated. Although their proposed volumetric law provides a good fit to a large range of data, the evaluation of _ff requires that a scaleheight for the gas be assumed and this is not easily derived from the observations so the quality of fit is largely dependent on what is assumed.

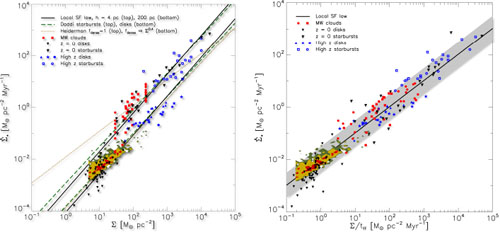Figure 8.19. Left panel shows the compilation of observational determinations of the SFR and total gas surface densities by Krumholz et al. (2012) together with several proposed SFR prescriptions. The right panel shows the alignment of these data improved when the gas surface densities are normalised by a free-fall timescale, i.e., a scalelength, to provide a fixed `volumetric' law.

8.3.4. Distinguishing normal star formation and starbursts: concentration and timescales

How does one define a starbursting system (as opposed to a normal star-forming galaxy) and what are the observational discriminants between these two modes? I think the most physically meaningful definition for a starburst is a galaxy or area within a galaxy where the rate of conversion of existing ISM into stars is such that the ISM will be consumed in a time significantly less than the typical M_ISM / SFR 1 Gyr timescale for local galaxies like the Milky Way. This SFE can be observationally characterised by the simple ratio L_IR / M_H2.

Alternatively, one might use the specific SFR per unit stellar mass (SSFR = SFR / M_*) to identify galaxies where the characteristic timescale (1/SSFR) is much shorter than the `likely' age of the galaxy (which is obviously less than the age of the Universe at the galaxy's redshift). At redshift z = 1.5-2.5, Rodighiero et al. (2011) argue that there is a tight `main sequence' of star-forming galaxies with fairly constant SSFR at all stellar masses (see Fig. 8.29); they then identify starburst objects with SSFR significantly above this main sequence. Unfortunately, the SSFRs found for the main sequence at z ~ 2 are higher by a factor ~ 15 than those at low redshift so the discriminant between the two star formation modes is evolving in time - without a clear physical basis, be it a higher gas content, smaller stellar mass at early epochs or an increasing efficiency/rate in converting existing gas to stars. And, of course, if the definition of the main sequence is evolving in time, the fraction of galaxies found to be `bursting' will depend entirely on how far off the main sequence a galaxy must be to be so classified. If most galaxies at high redshift were, in fact, bursting, then the `main-sequence' SSFR would be elevated as observed and the dispersion would simply reflect the range of burst activity. Clearly, it would be most important now to analyse the morphologies of the so-called main-sequence galaxies to classify the merging/interacting versus undisturbed percentages.

Definitions for starburst classification which compare the SSFR to the galaxy age or better, using the timescale for exhausting the ISM are more physically based than simply using the dispersion about the main sequence. In the near future we can anticipate that ALMA will be measuring gas contents for large samples of high-z galaxies.

Another approach which might be used to identify starburst activity is the luminosity density or concentration of the activity. In starbursting systems, one expects that a large fraction of the luminosity from the young stars will be absorbed by dust and emerge in the FIR and that the luminosity energy density within the active region will be high. As discussed in Section 8.2.9, good IR SED sampling allows one to classify the observed SED according to the ratio L_IR / M_dust which is proportional to L_IR / M_ISM. Sources with high luminosity density (either AGN or intense starbursts) may also have high `apparent' colour temperatures, providing they are not completely enshrouded by dust which is optically thick out to 100 µm. One can reasonably estimate a characteristic source size using Equation 8.13 and a luminosity density from L_IR / (4 R_thick³ / 3).

8.3.5. Starbursts in ULIRGs

In Fig. 8.20 the SEDs, L_IR / M_H2 mass ratios and fitted dust temperatures are shown for the complete sample of 20 ULIRGs at z < 0.1 from Sanders et al. (1988) and Sanders et al. (1991). The SEDs peak at 120 µm with dust colour temperatures 30-50 K and the FIR-to-H₂ mass ratios are 30-200 L / M. As noted above, these ratios are a factor 10-20 higher than the luminosity-to-mass ratios in local spiral galaxies, indicating a 10-20 times shorter timescale for converting ISM to young stars.

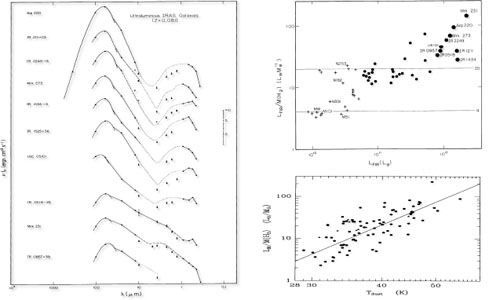Figure 8.20. The SEDs, LIR / MH2 mass ratios and fitted dust temperatures are shown for the complete sample of 20 ULIRGs at z < 0.1 from Sanders et al. (1988) and Sanders et al. (1991).

8.3.6. Arp 220 - a prototypical ULIRG

In the spirit of `one example can provide more understanding than many generalisations', I think it is very worthwhile to look in detail at current observations of Arp 220. Of course not all ULIRGs are the same as Arp 220, but one can readily see the essence of the starburst mode in this object.

Arp 220, at 77 Mpc, is one of the nearest and the best-known ultra-luminous merging system (L_{8-1000 µm} = 1.5 × 10¹² L). To power the IR output, star formation must be occurring at a rate of ~ 10² M yr^-1. Visual wavelength images reveal two faint tidal tails, indicating a recent tidal interaction (Joseph & Wright 1985), and high-resolution ground-based radio and NIR imaging show a double nucleus (Baan & Haschick 1995; Graham et al. 1990). The radio nuclei are separated by 0.98 arcsec (Baan & Haschick 1995), corresponding to 350 pc. Millimetre-wave imaging provides a unique capability to probe such starburst nuclei in dusty LIRG/ULIRGs since the dust is optically thin at long wavelengths. Virtually all of the ULIRGs observed so far have massive concentrations of molecular gas in the central few kiloparsec (Scoville et al. 1997; Downes & Solomon 1998; Bryant & Scoville 1999; Tacconi et al. 1999).

Arp 220 has been imaged at high resolution in the 2.6 mm CO line (Scoville et al. 1991), 3 mm HCN (Radford et al. 1991), 1.3 mm CO (Scoville et al. 1997; Downes & Solomon 1998; Tacconi et al. 1999) and most recently in the 0.9 mm CO and HCO⁺ lines (Sakamoto et al. 2009). The CO(2-1) line emission exhibits two peaks separated by 0.9 arcsec, and a larger inclined disk of molecular gas (Scoville et al. 1997; Downes & Solomon 1998; Sakamoto et al. 1999; Tacconi et al. 1999). At 0.5 arcsec resolution (Sakamoto et al. 1999), the CO and 1.3 mm continuum imaging shown in Fig. 8.21 reveals counter-rotating disks of gas in each of the IR nuclei. The kinematic data require very high mass concentrations in both of the nuclei. The nuclear disks are counter-rotating, consistent with the notion that the most complete and violent merging should be associated with counter-rotating precursor galaxies in which there is naturally angular momentum cancellation during the merging. The masses of each nucleus are apparently dominated by the molecular gas - a common finding of the ULIRG galaxy studies (Bryant & Scoville 1999). The nucleus of Arp 220 has a total molecular gas mass M_H2 ~ 9 × 10⁹ M within 300 pc (Scoville et al. 1997; Downes & Solomon 1998; Sakamoto et al. 1999; Tacconi et al. 1999). This H₂ mass within 300 pc is 3-4 times that of the entire Milky Way (most of which is in the ring at 4-8 kpc).

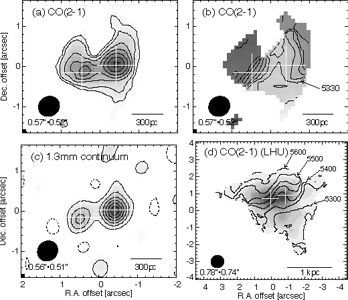Figure 8.21. The merging galactic nuclei of Arp 220 are shown in 0.5 arcsec resolution imaging of the CO(2-1) and dust continuum emission (Sakamoto et al. 1999). The four panels show: a) continuum-subtracted CO(2-1), b) the CO mean velocities, c) the 1.3 mm dust continuum, and d) the total CO emission including the extended molecular emission. These data resolve the two nuclei (separated by 1 arcsec E-W or 350 pc) and the crosses indicate the 1.3 mm dust continuum peaks. In the molecular gas emission, the two galaxy nuclei have counter-rotating disks as seen in the upper-right image.

Although Arp 220 has enormous masses of molecular gas, one should not visualise this gas being contained in self-gravitating GMCs like those in the Galaxy. The high brightness temperature of the observed CO emission (Scoville et al. 1997) requires that the gas distribution be continuous, i.e., filled nuclear disks, not a cloudy medium. The mass density within the disks implies a visual extinction A_V ~ 2000 mag perpendicular to the disks! Clearly, studying such regions can only be superficial in the optical/NIR and must rely on much longer-wavelength observations.

The western nucleus in Arp 220 exhibits hard X-ray emission (Iwasawa et al. 2005) and very high-velocity CO emission. The inner dust emission source seen at ~ 1 is extremely compact with 10⁹ M within R < 35 pc (Downes & Eckart 2007). Downes & Eckart argue that the inferred dust temperature of ~ 175 K implies a higher radiation energy density for its heating than could be provided by a compact starburst and therefore that this nucleus may harbour a luminous and massive black hole.

8.3.7. An aside: Sgr A^* - an extraordinary ISM

Given the very limited spatial resolution in observations of distant nuclei such as Arp 220, it is instructive and cautionary to look at the properties of the ISM in our own Galactic nucleus despite the fact that it is not currently very active. The massive black hole associated with the radio source Sgr A^* has a mass of 4 × 10⁶ M - derived from the motions of stars within the central 1 pc (Genzel 2006; Ghez 2007). A circumnuclear disk (CND) at radius out to ~ 3 pc is seen with both ionised gas and dense molecular clumps on the exterior. Figure 8.22 shows the ionised gas as probed in the Hi P line at 1.87 µm (greyscale; Scoville et al. 2003) in a structure termed the mini-spiral and the dense molecular gas as probed in the 3 mm HCN line (contours; Christopher et al. 2005). The molecular gas is in a clumpy ring at 1-3 pc radius. The ionised gas in the mini-spiral may be infalling or outflowing; the ionised gas at the edge of the disk in the southeastern arm probably arises from photoionisation at the inner edge of the molecular cloud ring.

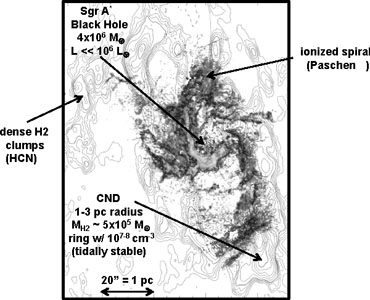Figure 8.22. The circumnuclear disk (CND) in the Galactic nucleus disk in ionised gas (greyscale) as imaged in the Hi P line at 1.87 µm (Scoville et al. 2003) and the dense molecular gas (contours) seen in HCN emission (Christopher et al. 2005). The ionised gas is distributed in a `spiral' pattern and at the inner surfaces of the neutral molecular clumps. The densities in the molecular gas are ~ 107-8 cm-3(!), orbiting at 1-3 pc radius.

The total mass of the molecular gas within 3 pc of the black hole is variously estimated at 1-5 × 10⁵ M and has an orbital time ~ 10⁵ yr. Given that the black hole is only ~ 10 times more massive it is clear that very little of the nearby ISM will actually make it to the black hole, unless we are viewing an extremely atypical epoch for Sgr A^*. In any case, it is certainly the case that the ISM here is not being accreted on an orbital timescale since the luminosity of Sgr A^* is ≪ 10⁶ L.

Just as was the case for Arp 220, our intuition about the properties of the ISM in the disk of our galaxy (i.e., self-gravitating GMCs) clearly cannot be transferred directly to the ISM in the Milky Way nucleus. The molecular gas clumps in the CND have extraordinary properties! Their sizes are < 1 pc but densities 10^7-8 cm^-3 (Christopher et al. 2005). (By contrast, a typical Galactic 10⁵ M GMC has a diameter 40 pc and mean density ~ 300 cm^-3, see Section 8.1.3). The higher densities are required near Sgr A^* if the clumps are to be stable against tidal disruption, given their proximity to the central point mass. If the dust-to-gas ratio in the clumps is similar to the standard Galactic value, then the inferred column densities of 10²⁵ cm^-2 imply an extinction of A_V 10⁴ mag through each clump. Since the molecular ring/torus is clearly not appearing edge-on, its angular momentum is not perpendicular to the Galactic plane. The ring therefore probably resulted from the accretion and disruption of a single cloud at non-zero height out of the Galactic plane, rather than smooth accretion over time from the larger nuclear disk. If such a cloud arrived at the point where it was tidally disrupted with a non-zero height the resulting fragments might end up as clumps in an orbital plane inclined to the Galactic plane, as is observed for the CND.

At present there is no evidence of star formation within the molecular clumps despite their very high densities and extraordinarily short internal dynamical timescales ~ 10⁴ yr. However, the very high extinctions suggested above would preclude detection of embedded young stars and the only means of detecting them might be via radio detection of ultra-compact Hii regions or maser emission. The unusually high densities of the molecular clumps must reflect the fact that at lower density they would not be tidally stable and therefore could not exist for long (see Section 8.3.8).

8.3.8. Nuclear starburst disks

As a first step toward understanding the massive gas disks like that seen in Arp 220, we consider an extremely simple model with uniform gas surface density out to radius 100 pc. At the centre of the disk, we assume a point mass of 4 × 10⁸ M - either a central black hole or a nuclear star cluster. The disk is assumed to be self-gravitating and in hydrostatic equilibrium with a sound speed of 50 km/s, representative of the turbulent velocity dispersion measured in Arp 220. Although this is meant only as an illustrative, gedanken, experiment, it clearly shows that the conditions are inescapably different from those of star-forming clouds in the Galactic disk.

In Fig. 8.23, the disk thickness and mean gas densities are shown as a function of radius out to 100 pc. The thickness of the disk is typically less than 10 pc and the mean densities are everywhere > 10⁶ cm^-3, getting up to 10¹⁰ cm^-3 near the centre. The right panel of Fig. 8.23 also shows the gas density required for tidal stability (dashed line) - clearly demonstrating that it will be difficult to form stable clouds within the central 10 pc radius. Within this region, we should expect a more continuous gaseous disk structure, not a cloudy ISM as found in the centre of our Galaxy.

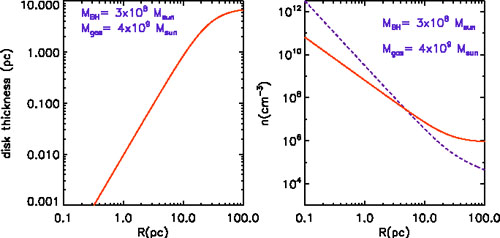Figure 8.23. A very crude model for the disk in gas-rich merging systems like Arp 220 is shown. We assume a central point mass (black hole) and a uniform gas surface density disk extending to 100 pc radius. The turbulent velocity dispersion within the disk is taken to be 50 km/s (based on Arp 220; Scoville et al. 1997). The disk thickness as a function of radius for hydrostatic equilibrium is shown in the right panel and the mean gas density in the left panel (solid red line). The critical density required for stability of a self-gravitating object (e.g., a cloud) in the disk is shown by the dashed (blue) curve. The right panel shows the extraordinarily high gas densities expected for these very simple assumptions and underscores the fact that self-gravitating clouds should not form in the inner disk due to tidal disruption.

The gravitational stability of the disk can also be seen from the Toomre Q parameter shown in Fig. 8.24 (left panel). Within the inner 10 pc, Q ≫ 1 and it is very hard to form self-gravitating structures in the ISM, such as clouds. On the other hand, outside 10 pc radius such clouds might form (if they are not disrupted by cloud collisions) but their masses are required to be very large, exceeding 10⁶ M.

Figure 8.24. The left panel shows the Toomre Q stability parameter (Q < 1 unstable) for the disk parameters in the previous figure and the right panel shows the Jeans mass for collapse/self-gravitation assuming a sound speed of 50 km/s and neglecting tidal shear.

8.3.9. Maximum-rate starbursts - the dust Eddington limit

For Arp 220, the estimated nuclear SFR of 100-200 M per year is at least a factor of ten less than the maximal rate, obtained by dividing the ISM by the orbital timescale of ~ 2 × 10⁶ yr. One very effective means of restricting the star fromation (or even ejecting the dense ISM) is via the radiation pressure on dust of the central starburst (or AGN) luminosity. For a self-gravitating gas and dust mass, the effective `Eddington' limit is approximately 500 L / M, similar to the overall mass-to-light ratio measured in the Arp 220 nucleus (10¹² L / 3 × 10⁹ M). For higher luminosity-to-mass ratios, the ISM is blown out of the region.

The significant role of radiation pressure in high-mass star formation and starbursts for feedback through radiation pressure on buildup has only recently been appreciated. The outward radiation pressure in a starbursting cloud core or galactic nucleus will dominate self-gravity at radius R when

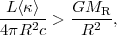(30)

where < > is the effective radiative absorption coefficient per unit mass. Although the original stellar radiation is primarily UV and visible, the dust in the cloud core absorbs these photons and re-radiates the luminosity in the IR. The `effective' absorption coefficient takes account of the fact that outside the radius where A_V ~ 1 mag, the luminosity is at longer wavelengths where the dust has a reduced absorption efficiency. For the standard ISM dust-to-gas ratio (Draine & Li 2007), A_V = 1 mag corresponds to a column density N_H = 2 × 10²¹ cm^-2 and

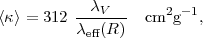(31)

where _eff(R) is the absorption coefficient-weighted mean wavelength of the radiation field at radius R and for simplicity, we have adopted a ^-1 wavelength dependence for the absorption efficiency.

Combining Equations 8.30 and 8.31, we find that the radiation pressure will exceed the gravity when

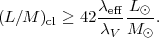(32)

For _eff ~ 3-10 µm, _eff / _V is approximately 10 and the radiation pressure limit is ~ 500 L / M. Thus, for luminosity-to-mass ratios exceeding this value radiation pressure will halt further accretion. For a forming OB star cluster, this luminosity-to-mass ratio is reached at about the point where the upper main sequence is first fully populated, i.e., a cluster with approximately 2000 M distributed between 1 and 120 M. A similar `Eddington' limit applies for any dust-embedded starburst region (see Scoville et al. 2001; Scoville 2003; Murray et al. 2005; Thompson et al. 2005). It turns out that much larger-scale nuclear starbursts such as that in Arp 220 have approximately reached the same empirical limit of 500 L / M, suggesting that nuclear starburst activity may also be regulated by a balance of self-gravity and radiation pressure support.

8.3.10. AGN - starburst: observational connections

Evidence has also accumulated for an evolutionary link between merging ULIRGs and UV/optical quasi-stellar objects (QSOs) as suggested by Sanders et al. (1988): similar local space densities for ULIRGs and QSOs; continuity of FIR SEDs smoothly transitioning between the two classes; the occurrence of AGN-like emission lines (Veilleux et al. 1999) and significant point-like nuclei (less than 0.2 arcsec - Scoville et al. 2000) in 30-40% of the ULIRGs; and the association of both ULIRGs and some QSOs (MacKenty & Stockton 1984; Bahcall et al. 1997) with galactic interactions (see the review article by Sanders & Mirabel 1996). Whether the entire QSO population had precursor ULIRGs (implying that galactic merging is the predominant formation mechanism for AGN) is certainly not yet settled and at lower AGN luminosities, much of the activity is probably not directly associated with galaxy merging or interactions.

Two possible scenarios linking the ULIRG and luminous AGN phenomena are: 1) that the abundant ISM, deposited in galactic nuclei by merging, fuels both the nuclear starburst and feeds the central black hole accretion disk; or alternatively, 2) the post-starburst stellar population evolves rapidly with a high rate of mass return to the ISM in the galactic nucleus - leading to sustained fuelling of the black hole (e.g., Norman & Scoville 1988).

8.3.11. AGN - starburst: theoretical connections

The largest potential sources of fuel for AGN are the nuclear ISM (until it has been cleared out) and the mass loss associated with normal stellar evolution of stars in the galactic nucleus. Most recent discussion has assumed the former link; so I would like to briefly discuss the latter possibility here - partially as a stimulus for further investigation by students. For a nuclear starburst population, approximately 20% of the initial stellar mass will be lost via red giant mass-loss winds within the first 2 × 10⁸ years (Norman & Scoville 1988). (The mass return associated with supernovae is probably significantly less.) Scoville & Norman (1988) and Scoville & Norman (1995) examined the fate of this mass-loss material - specifically to account for both the broad emission lines (BELs) and the broad absorption lines (BALs) seen in AGN. Since the stars will not be disrupted by AGN feedback once the nucleus becomes active, the stars can provide a long-term supply of fuel to power the AGN.

The physics of the dust shed by the stars in their stellar winds, particularly its evaporation, is critical to determining whether the mass-loss material accretes inwards to an accretion disk or is blown outwards by radiation pressure. This consideration leads naturally to a division of the central cluster environment into: 1) an inner zone (r 1 pc) where the dust is heated to above the sublimation temperature and the lower opacity of the dust-free gas allows it to fall inwards, and 2) an outer zone (r 1 pc) where the dust (and gas) survives and is driven outwards at velocities up to 0.1c by radiation pressure.

It is interesting to note that the density required for tidal stability of a BEL cloud at 1 pc radius from the black hole requires that the clouds must have extremely high internal densities. At 1 pc from a 10⁹ M black hole, the Roche limit density is 3 × 10¹¹ cm^-3. This provides a strong argument for the stellar (rather than interstellar) scenario to account for the BELs, using the stellar masses to bind the emission line gas.