Annu. Rev. Astron. Astrophys. 2002. 40: 319-348 Copyright © 2002 by Annual Reviews. All rights reserved

4. INVERSE COMPTON X-RAY EMISSION

Cosmic magnetic fields can be derived by comparing inverse Compton X-ray emission and radio synchrotron radiation (Harris & Grindlay 1979, Rephaeli, Gruber, & Rothschild 1987). Inverse Compton (IC) emission is the relativisitic extrapolation of the Sunyaev-Zel'dovich effect (Rephaeli 1995), involving up-scattering of the ambient photon field by the relativisitic particle population. The IC process involves two Lorentz transforms (to and from the rest frame of the electron), plus Thompson scattering in the rest frame of the electron, leading to _IC ~ 4/3 ² _bg, where _IC is the emergent frequency of the scattered radiation, is the electron Lorentz factor, and _bg is the incident photon frequency (Bagchi, Pislar, & Lima Neto 1998). From a quantum mechanical perspective, synchrotron radiation is directly analogous to IC emission, with synchrotron radiation being the up-scattering of the virtual photons that constitute the static magnetic field. Given a relativistic electron population, the IC emissivity is directly proportional to the energy density in the photon field, U_bg, while the synchrotron emissivity is proportional to the energy density in the magnetic field, U_B, leading to a simple proportionality between synchrotron and IC luminosity: L_syn / L_IC U_B / U_bg. Given that they originate from the same (assumed power-law) relativistic electron population, IC X-rays and synchrotron radio emission share the same spectral index, . The spectral index relates to the index for the power-law electron energy distribution, , as = 2 - 1, and to the photon index as - 1.

In most astrophysical circumstances U_bg is dominated by the cosmic microwave background (CMB), except in the immediate vicinity of active star forming regions and AGN (Brunetti et al. 2001a, Carilli et al. 2001). The Planck function at T = 2.73 K peaks near a frequency of _bg ~ 1.6 × 10¹¹ Hz, hence IC X-rays observed at 20 keV (_IC = 4.8 × 10¹⁸ Hz), are emitted predominantly by electrons at ~ 5000, independent of redshift ¹. The corresponding radio synchrotron emission from = 5000 electrons peaks at a (rest frame) frequency of _syn ~ 4.2 (B / (1 µG)) ² Hz = 100 MHz (Bagchi, Pislar, & Lima Neto 1998).

Many authors have considered the problem of deriving magnetic fields by comparing synchrotron radio and inverse Compton X-ray emission (Blumenthal & Gould 1970, Harris & Grindlay 1979, Rephaeli, Gruber, & Rothschild 1987, Feigelson et al. 1995, Bagchi, Pislar, & Lima Neto 1998). Assuming = -1, the magnetic field is given by:

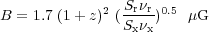(4)

where S_r and S_x are the radio and X-ray flux densities at observed frequencies _r and _x, respectively. Note that, unlike Faraday rotation measurements, the geometry of the field does not play a critical role in this calculation, except in the context of the electron pitch angle distribution (see Section 4.2).

The principle difficulty in studying IC emission from clusters of galaxies is confusion due to the thermal emission from the cluster atmosphere. One means of separating the two emission mechanisms is through spectroscopic X-ray observations at high energy. The IC emission will have a harder, power-law spectrum relative to thermal brehmstrahlung emission. Recent high energy X-ray satellites such as Beppo/Sax and RXTE have revolutionized this field by allowing for sensitive observations to be made at energies well above 10 keV (Rephaeli 2001). Prior to these instruments, most studies of IC emission from clusters with radio halos only provided lower limits to the magnetic fields of about 0.1 µG (Rephaeli, Gruber, & Rothschild 1987).

Recent observations of four clusters with radio halos with Beppo/Sax and RXTE have revealed hard X-ray tails which dominate the integrated emission above 20 keV (Rephaeli, Gruber, & Blanco 1999, Fusco-Femiano et al. 2001, Fusco-Femiano et al. 2000). In Fig. 7 we reproduce the RXTE observations of the Coma cluster. The hard X-ray emission in these sources has a spectral index = -1.3 ± 0.3, roughly consistent with the radio spectral index. Comparing the IC X-ray and radio synchrotron emission in these sources leads to a volume averaged cluster magnetic field of 0.2 to 0.4 µG, with a relativistic electron energy density ~ 10^-13 erg cm^-3.

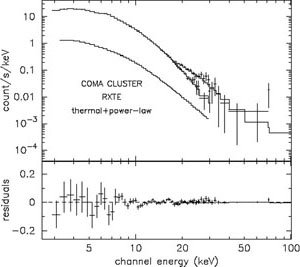Figure 7. RXTE spectrum of the Coma cluster. Data and folded Raymond-Smith (kT 7.51 keV), and power-law (photon index = 2.34) models are shown in the upper frame; the latter component is also shown separately in the lower line. Residuals of the fit are shown in the lower frame (Rephaeli 2001).

Spatially resolving X-ray observations can also be used to separate non-thermal and thermal X-ray emission in clusters. This technique has been used recently in the study of the steep spectrum radio relic source in Abell 85 (Bagchi, Pislar, & Lima Neto 1998). An X-ray excess relative to that expected for the cluster atmosphere is seen with the ROSAT PSPC detector at the position of the diffuse radio source in Abell 85 (see Fig. 8). Bagchi, Pislar, & Lima Neto (1998) subtract a model of the thermal cluster X-ray emission in order to derive the IC contribution, from which they derive a magnetic field of 1.0 ± 0.1 µG.

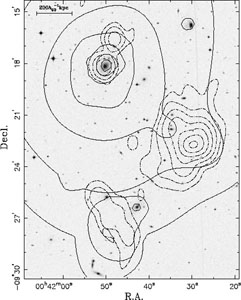Figure 8. The cluster Abell 85 central region at different wavelengths. The photographic R-filter image (UK Schmidt Telescope and the Digitized Sky Survey) is shown in grey scale. Full contour lines show the multiscale wavelet reconstruction of the ROSAT PSPC X-ray data shown in Fig. 1. The OSRT 326.5 MHz radio surface-brightness image is depicted using dot-dashed contour lines. All contours are spaced logarithmically (Bagchi, Pislar, & Lima Neto 1998).

Emission above that expected from the hot cluster atmosphere has also been detected in the extreme ultraviolet (EUV = 0.1 to 0.4 keV) in a few clusters (Berghöfer, Bowyer, & Korpela 2000, Bowyer, Korpela, & Berghöfer 2001, Bonamente et al. 2001). It has been suggested that this emission may also be IC in origin, corresponding to relativistic electrons with ~ 400 (Atoyan & Völk 2000). However, the emission spectrum is steep ( -2), and the EUV emitting regions are less extended than the radio regions. Neither of these properties are consistent with a simple extrapolation of the radio halo properties to low frequency (Bowyer, Korpela, & Berghöfer 2001). Also, the pressure in this low relativistic component would exceed that in the thermal gas by at least a factor of three (Bonamente et al. 2001).

4.1. Electron lifetimes

An important point concerning IC and synchrotron emission from clusters is that of particle lifetimes. The lifetime of a relativistic electron is limited by IC losses off the microwave background to: t_IC = 7.7 × 10⁹ (300 / ) (1 + z)^-4 years (Sarazin 2001a). ² Relativistic electrons emitting in the hard X-ray band via IC scattering of the CMB have lifetimes of about 10⁹ years, while the lifetimes for 1.4 GHz synchrotron emitting electrons are a factor of four or so shorter in µG fields. Diffusion timescales (set by streaming along the tangled magnetic field) for cluster relativistic electrons are thought to be longer than the Hubble time (Sarazin 2001a, Colafrancesco & Blasi 1998, Casse, Lemoine & Pelletier 2001), making cluster atmospheres efficient traps of relativistic electrons, much like galaxy disks. The fact that the diffusion timescales are much longer than the energy loss timescales for > 10⁴ electrons requires in situ acceleration in order to explain radio halo sources (Schlikeiser, Sievers, & Thiemann 1987).

Cluster merger shock fronts are obvious sites for first order Fermi acceleration, while subsequent turbulence may lead to second order (stochastic) Fermi acceleration (Brunetti et al. 2001b, Eilek 1999, Ensslin et al. 1998, Markevitch & Vikhlinin 2001). Active particle acceleration during cluster mergers provides a natural explanation for the observed correlation between cluster radio halos and substructure in cluster atmospheres (Govoni et al. 2001a), and between cluster radio luminosity and cluster atmosphere temperature, assuming that the gas temperature increases during a merger (Liang et al. 2000). Brunetti et al. (2001a) develop a two phase model in which initial relativistic particle injection into the ICM occurs early in the cluster lifetime by starburst driven winds from cluster galaxies, and/or by shocks in early sub-cluster mergers. The second phase involves re-acceleration of the radiatively aged particle population via more recent cluster mergers. Their detailed application of this model to the Coma cluster suggests a merger has occurred within the last 10⁹ years.

Another mechanism proposed for in situ relativistic particle injection is secondary electron production via the decay of -mesons generated in collisions between cosmic ray ions (mostly protons) and the thermal ICM (Dennison 1980, Ensslin & Gopal-Krishna 2001). The important point in this case is that the energetic protons have radiative lifetimes orders of magnitude longer than the lower mass electrons. The problem with this hypothesis is that the predicted -ray fluxes exceed limits set by EGRET by a factor of 2 to 7 (Blasi & Colafrancesco 1999).

4.2. Reconciling IC and RM-derived fields

The IC estimated cluster magnetic fields are typically 0.2 to 1 µG, while those obtained using RM observations are an order of magnitude higher. Petrosian (2001) has considered this discrepancy in detail, and finds that the different magnetic field estimates can be reconciled in most cases by making a few reasonable assumptions concerning the electron energy spectrum and pitch angle distribution.

First, an anisotropic pitch angle distribution biased toward low angles would clearly weaken the radio synchrotron radiation relative to the IC X-ray emission. Such a distribution will occur naturally due to the fact that electrons at large pitch angles have greater synchrotron losses. A potential problem with this argument is that pitch-angle scattering of the relativistic electrons by Alfven waves self-induced by particles streaming along field lines is thought to be an efficient process in the ISM and ICM (Wentzel 1974), such that re-isotropization of the particle distribution will occur on a timescale short compared to radiative timescales. Petrosian points out that most derivations of magnetic fields from IC emission assume the electrons are gyrating perpendicular to the magnetic field lines. Just assuming an isotropic relativistic electron pitch angle distribution raises the IC-estimated magnetic field by a factor of two or so.

And second, the IC hard X-ray emission is from relativistic electrons with ~ 5000, corresponding to radio continuum emission at 100 MHz for µG magnetic fields. Most surveys for cluster radio halos have been done at 1.4 GHz (Giovannini, Tordi & Feretti 1999, Govoni et al. 2001a), corresponding to electron Lorentz factors of ~ 18000. A steepening in the electron energy spectrum at Lorentz factors around 10⁴ will reduce the 1.4 GHz radio luminosities, but retain the IC hard X-ray emission. For example, Petrosian finds that a steepening in the power-law index for the particle energy distribution from = -3 to = -5 (corresponding to = -1 to -2) at ~ 10⁴ raises the IC-estimated fields to ~ 1µG. Such a steepening of the electron energy spectrum at ~ 10⁴ will arise naturally if no relativistic particle injection occurs over a timescale ~ 10⁸ years (see Section 4.1). The problem in this case is the fine tuning required to achieve the break in the relevant energy range for a number of clusters. In general, a negatively curved (in log-space) electron energy distribution will inevitably lead to IC estimated fields being lower than those estimated from 1.4 GHz radio observations, unless a correction is made for the spectral curvature.

Others have pointed out that magnetic substructure, or filamentation, can lead to a significant difference between fields estimated using the different techniques. A large relativistic electron population can be 'hidden' from radio observations by putting them in weak field regions (Feretti et al. 2001, Rephaeli, Gruber, & Rothschild 1987, Rephaeli 2001, Goldshmidt & Rephaeli 1993, Rudnick 2000). A simple example of this is if the relativistic particles have a larger radial scale-length than the magnetic fields in the cluster. In this case, most of the IC emission will come from the weak field regions in the outer parts of the cluster, while most of the Faraday rotation and synchrotron emission occurs in the strong fields regions in the inner parts of the cluster.

Another explanation for the discrepancy between IC and RM derived magnetic fields is to assume that the hard X-rays are not IC in origin, in which case the IC estimates become lower limits. A number of authors have considered high energy X-ray emission due to non-thermal Brehmstrahlung, i.e. Brehmstrahlung radiation from a supra-thermal tail of electrons arising via stochastic acceleration in a turbulent medium (Fermi II acceleration) (Blasi 2000, Sarazin 2001a, Ensslin & Gopal-Krishna 2001, Dogiel 2000). The problem with this hypothesis is the energetics: Brehmstrahlung is an inefficient radiation mechanism, with most of the collisional energy going into heat. Assuming an energy source is available to maintain the supra-thermal tail, Petrosian (2001) shows that the collisional energy input by the supra-thermal particles would be adequate to evaporate the cluster atmosphere on a timescale of order 10⁸ years.

The current hard X-ray spectroscopic observations are limited to very low spatial resolution (~ 1°), while X-ray imaging instruments have high energy cut-offs at around 10 keV. Likewise, sensitive, arcminute resolution radio images for a large number of clusters are available only at 1.4 GHz, corresponding to electrons with Lorentz factors 3 to 4 times higher than those emitting hard X-rays. Both of these limitations will be overcome in the coming years with the launch of hard X-ray imaging satellites such as Constellation-X, and improvements in radio imaging capabilities at 300 MHz and below at the Very Large Array and the Giant Meter Wave Radio Telescope.

¹ is independent of redshift since _bg increases as 1 + z. Back.