Annu. Rev. Astron. Astrophys. 2002. 40: 319-348 Copyright © 2002 by Annual Reviews. All rights reserved

5. COLD FRONTS

It has long been noted that in order to maintain temperature gradients in X-ray clusters the thermal conduction must be suppressed by two orders of magnitude relative to the classical Spitzer value (McKee & Begelman 1990, Fabian 1994, Spitzer 1962). If not, cooler structures on scales ~ 0.1 Mpc will be evaporated by thermal conduction from the hot surrounding medium on timescales ~ 10⁷ years. Examples of such cooler structures in clusters include cooling flow cluster cores and X-ray corona surrounding large galaxies (Fabian 1994, Vikhlinin et al. 2001b), with temperature differences ranging from a factor of 2 to 5 relative to the hot ICM.

Cowie & McKee (1977) show that the conductivity can be suppressed by almost an order of magnitude below the Spitzer value due to the development of electrostatic fields in cases where the Coulomb mean free path (mfp) is comparable to the scale of thermal gradients. For large scale structure in cluster atmospheres this reduction is not adequate since the mfp ~ 1.2 × 10²² (T / (5 × 10⁷ K))² (n / (0.001 cm^-3))^-1 cm, or just a few kpc for a typical cluster.

The presence of magnetic fields will reduce the conductivity in a thermal plasma (Field 1965, Parker 1979, Binney & Cowie 1981, Chandran, Cowley, & Albright 1999). The simple point is that the gyro radius for thermal electrons in the ICM is ~ 2 × 10⁸ (B / (1 µG))^-1 (T / (5 × 10⁷ K)) cm, many orders of magnitude below the collisional mfp. Tribble (1993) shows that the presence of a cluster magnetic field will lead naturally to the development of a multiphase ICM, with thermally isolated regions on scales set by the magnetic structures (although cf. Rosner & Tucker 1989).

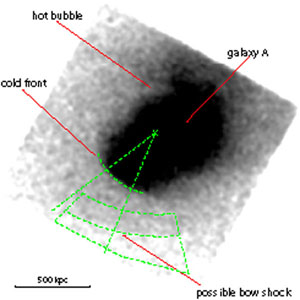
The idea of magnetic suppression of thermal conductivity in cluster gas has been verified with the recent discovery of `cold fronts' in clusters of galaxies (Markevitch et al. 2000, Vikhlinin et al. 2001b, Vikhlinin et al. 2001a). These fronts manifest themselves as sharp discontinuities in X-ray surface brightness (Fig. 9). They are not shocks, since the increase in density is accompanied by a decrease in temperature such that there is no dramatic change in the pressure and entropy across the front (Markevitch et al. 2000, Ettori & Fabian 2000). These structures are interpreted as resulting from cluster mergers, where a cooler subcluster core falls into a hot ICM at sub- or trans-sonic velocities (~ 10³ km s^-1). A discontinuity is formed where the internal pressure of the core equals the combined ram and thermal pressure of the external medium. Gas beyond this radius is stripped from the merging subcluster, and the core is not penetrated by shocks due to its high internal pressure.

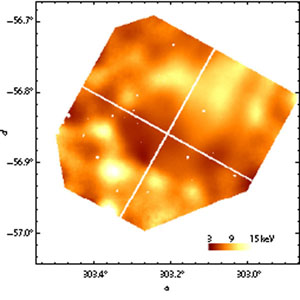Figure 9. (a) A smoothed 0.5-4 keV Chandra image of Abell 3667. The most prominent feature is the sharp surface brightness edge (cold front). The front shape is nearly circular as indicated by the arc. (b) Temperature map. The typical statistical error in this image is ± 1 keV. The cold, ~ 4 keV, region near the center of the map coincides with the inside of the cold front (Vikhlinin et al. 2001a).

The best example of a cluster cold front is that seen in Abell 3667 (see Fig. 8) (Vikhlinin et al. 2001b, Vikhlinin et al. 2001a). In this case, the temperature discontinuity occurs over a scale of ~ 5 kpc, comparable to the collisional mfp, thereby requiring thermal isolation. Magnetic fields play a fundamental role in allowing for such structures in two ways: (i) by suppressing thermal conduction, and (ii) by suppressing Kelvin-Helmholtz mixing along the contact discontinuity. Vikhlinin et al. (2001a) present a model in which the field is tangentially sheared by fluid motions along the contact discontinuity. They invoke magnetic tension to suppress mixing, and show that the required magnetic pressure is between 10% and 20% of the thermal pressure. The implied fields are between 7 and 16 µG. They also argue that the fields cannot be much stronger than this, since dynamically dominant fields would suppress mixing along the entire front, which does not appear to be the case.

The existence of cold fronts provides strong evidence for cluster magnetic fields. However, the field strengths derived correspond to those in the tangentially sheared boundary region around the front. Relating these back to the unperturbed cluster field probably requires a factor of a few reduction in field strength, implying unperturbed field strengths between 1 and 10 µG, although the exact scale factor remains uncertain (Vikhlinin et al. 2001a).