


A majority of disk galaxies contain a bar of some kind. Bars are clearly visible in some 30% of galaxies, as judged from SDSS galaxy images by the Galaxy Zoo project (Masters et al. 2011). A larger bar fraction is seen in near-infrared images (e.g. Eskridge et al. 2000; Menéndez-Delmestre et al. 2007), in part at least because bars can be obscured by star-forming regions in later type galaxies (e.g. Block & Wainscoat 1991). The bar fraction rises still further when weak oval distortions and short bars are included (e.g. Marinova & Jogee 2007; Reese et al. 2007). Yet even in these studies, some 30% of disk galaxies in the local universe still lack any trace of a bar.
The incidence of bars over cosmic time has been investigated in a number of studies, which face difficulties of morphological classification from small images, even with Hubble Space Telescope resolution, and of band shifting of the light distribution with redshift. Cameron et al. (2010), who reviewed previous work, concluded that the bar fraction in more massive galaxies has been constant since z ~ 0.6, but has increased in lower mass galaxies by about a factor of 2 over the same time interval. Sheth et al. (2012) also found that bars are less common in disturbed galaxies at high redshift. These findings seem consistent with a general picture that the bar fraction appears to be set after galaxies form and settle (Kraljic et al. 2012), which happens earlier in more massive galaxies. Bars are therefore believed to be old, long-lived structures.
Bars are also believed to have a greater extent normal to the disk plane than does the disk that hosts them, giving them a "peanut" shape when viewed edge on. Since we cannot see the face-on view in such cases, the evidence to support this interpretation of box-peanut bulges is indirect (e.g. Bureau & Athanassoula 2005). The inner Milky Way manifests such a shape (e.g. Blitz & Spergel 1991; Weiland et al. 1994; Strutskie 2006). In fact, its peanut shape is so pronounced that it is described as an "X shape" (McWilliam & Zoccali 2010; Nataf et al. 2010; Ness et al. 2012; Wegg & Gerhard 2013).
Sellwood & Wilkinson (1993) gave a thorough review of barred galaxies. Although somewhat dated, I refer the reader to that review for a detailed account, and give only a brief outline of the basic dynamics of bars here.
A self-consistent stellar bar has a nonlinear dynamical structure that is most easily visualized in a frame that rotates with the bar. A large fraction of the stars in a bar move in the forward sense in the rotating frame on elongated orbits that are confined to the bar. Clearly, moving forward in the rotating frame implies, in an inertial frame, an orbit period about the center that is shorter than the figure rotation period.
Most of the orbits within the bar occupy regular parts of phase space, in which the stars are trapped about periodic orbits, and there are a number of resonant families of such orbits. Figure 11 shows the most important orbit families in the midplane of an idealized rotating bar, which has the simple effective potential (cf. BT08 Eq. 3.103)
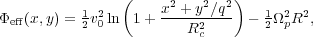 |
(27) |
where R2 = x2 +
y2, Rc is a core radius inside of
which the potential is approximately harmonic, q ≤ 1 is the
flattening, and v0 is the circular speed at large
R when q = 1. As in BT08, the
values are v0 = 1, q = 0.8,
Rc = 0.03, and
 p = 1.
p = 1.
Periodic orbits are described as resonant because they close in the bar-frame, and the solid curves show 2:1 families that close after two radial oscillations and one full turn about the center. The x1 family is described as the "backbone" of the bar (Contopoulos 1980), because the stars that are trapped around these orbits have a density distribution that is more elongated than the adopted bar potential. Since Poisson's equation requires the potential surfaces to be rounder than the density surfaces, the orbits that make up a self-consistent bar must be confined to a smaller region than is energetically accessible to them. This requires the majority of bar orbits to be regular, since chaotic orbits fill the volume bounded by their energy (or Jacobi constant, eq. 25).
Five Lagrange points occur in the bar potential, where a particle could remain stationary in the rotating frame. Four lie on the corotation circle, in an infinitesimal barlike potential: L1 and L2 lie on the bar major axis, L4 and L5 on the bar minor-axis, while L3 is at the bar center. In strong bars, L1 and L2 are closer to the center than are L4 and L5. The L1 and L2 Lagrange points in the potential used for Fig. 11 are very close to the points (x, y) = (± 1, 0),
Theorists generally agree that a self-consistent bar structure cannot extend farther from the center than the major-axis Lagrange points, because the stellar response outside corotation to forcing by a bar potential creates a density distribution that is elongated orthogonal to the bar direction. In addition, one cause of chaos in phase space is the overlap of resonances (Chirikov 1979), and the increasing density of resonances (see ultraharmonic resonances in Section 2.8) as corotation is approached led (Contopoulos 1980) to suggest that bars should end just before corotation. Elmegreen (1996) defined the useful dimensionless parameter
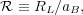 |
(28) |
which is the ratio of the distance, RL, of the
Lagrange point L1
(or L2) from the galaxy center to the semi-major axis of the bar,
aB, and thus Contopoulos's argument is that
 > 1 for all
bars. While there is no compelling theoretical argument against
> 1 for all
bars. While there is no compelling theoretical argument against
 ≫ 1, which would be
called a "slow bar", bar formation
models, and observational evidence from barred disk galaxies (see
Section 5.8) both indicate a strong preference for "fast
bars" that have
≫ 1, which would be
called a "slow bar", bar formation
models, and observational evidence from barred disk galaxies (see
Section 5.8) both indicate a strong preference for "fast
bars" that have 
 1.2, although some exceptions have been claimed.
1.2, although some exceptions have been claimed.
A second family of 2:1 orbits, known as the x2 family, is also illustrated in Fig. 11. These orbits are found only deep inside the bar and are elongated perpendicular to it. They generally appear only in models with dense centers, where the orbital periods are short. The forced response of near-circular orbits can be calculated analytically for an infinitesimal bar perturbation (BT08 eq. 3.147), from which it can be seen that the driven orbit orientation differs by 90∘ on opposite sides of all three major resonances (i.e. where l = 0, ±1 in Eq. 15). Orbit integrations are needed in strong bars, where the orientation shift can be regarded as the generalization of the ILR to large amplitude perturbations. The existence of an ILR in the potential of the azimuthally averaged mass distribution is a necessary, but not sufficient, condition for the appearance of the x2 family in a bar, since it can disappear as the bar strength is increased (Contopoulos & Papayannopoulos 1980). Even though the influence of the resonance can be recognized from the orbit structure, it is impossible to identify its location or radius in a strong bar because some x1 orbits, which align with the bar, overlap spatially with the perpendicularly oriented x2 orbits (Fig. 11).
The in-plane projections of many bars have distinctly "boxy" shapes (Kormendy 1983; Athanassoula et al. 1990; Gadotti 2011), suggesting that the parent orbits should have a somewhat rectangular shape. (The 3D shape is discussed later.) The dotted lines in Fig. 11 show three examples of 4:1 resonant orbits that are still elongated along the bar, whose existence may be related to the boxy shape of bars. Note that these orbits are found only close to corotation, where the orbit period in the rotating frame is long enough to allow four radial oscillations, and they therefore can be populated only in fast bars.
These 2:1, and perhaps also the 4:1, orbit families are the most important for bar dynamics, but many other less important orbit families have been found, even when motion is confined to a plane. The dynamics of motion in the third dimension is considerably richer (Pfenniger & Friedli 1991; Patsis et al. 2002; Skokos et al. 2002), with multiple commensurabilities possible between the vertical and in-plane frequencies. However, the most important orbits remain those that resemble the x1 family when seen in projection. Those that oscillate about the midplane in either an archlike structure or a figure of 8 when viewed from the side are 2:2:1 resonant orbits that complete two radial and two vertical oscillations for every turn about the center.
Note that the bar pattern speed is equal to the precession rate of the orbits that support it, and conversely all orbits precess at the bar pattern speed. In the absence of the bar potential, every orbit can still be regarded as a precessing ellipse (Kalnajs 1973), but the precession rates of the orbits would no longer be equal with the larger orbits generally precessing at lower rates than the smaller. Thus the effect of the bar potential is to impose a common precession rate on orbits that would otherwise prefer to precess at a range of different rates. Clearly, the stronger the bar potential, the greater its ability to trap orbits to precess with it. Because the bar is a self-consistent structure, its pattern speed can be regarded as an average, or "compromise," between the unforced precession rates of the orbits from which it is built. Thus bar pattern speeds must rise if mass accumulates in the bar center, since an increased mean density raises all orbital frequencies.
5.2.1. Global bar-forming mode
It has long been known from both numerical simulations (Hohl 1971; Ostriker & Peebles 1973) and global stability studies (Kalnajs 1972, 1978]; Jalali 2007), that simple models of rotationally supported stellar disks are globally unstable. In the linear regime, the instability takes the form of an open two-arm spiral but, as it saturates, the shape straightens into a bar in the inner disk, while the spiral in the outer disk winds up and disperses. Hohl (1971) showed that the instability causes considerable rearrangement of the angular momentum in the disk, 8 and the azimuthally-averaged mass profile is substantially changed, with the inner disk becoming denser, while material is also spread far outwards.
The vigorous linear instability that creates the nonlinear bar is the result of a cavity-type gobal mode, or standing wave, in a massive disk. The linear instability can arise only if the combined mass distribution of the dominant disk, plus contributions from any bulge and dark matter halo, yields a quasiharmonic potential over the inner part, so that the rotation curve rises roughly linearly from the center before flattening around a radius Rcore. In most circumstances, the group velocity (Toomre 1969) of trailing spiral waves is directed away from the corotation radius, while leading waves propagate toward it, as illustrated for a centrally cusped potential in Fig. 2. In that figure, the trailing disturbance was absorbed at an ILR, but an inwardly propagating trailing spiral can travel all the way to the galaxy center if it does not encounter this resonance, and an m = 2 disturbance easily avoids an ILR when the potential near the center is quasiharmonic. In that case, the incoming trailing wave reflects off the center into an outgoing leading spiral. The feedback loop is closed at corotation where the outgoing leading wave superreflects into an amplified trailing wave. At the same time, an outwardly propagating trailing wave is excited outside corotation that satisfies wave action conservation requirements. The mode is unstable because the wave train is amplified at corotation, and the instability typically exponentiates on the time scale of an orbital period.
The bar that results from this instability generally extends to a radius that is perhaps 20% – 30% greater than Rcore. The initial bar has a pattern speed that is often slightly lower than that of the eigenmode that caused it, and it almost fills its corotation circle. Thus bars are shorter in models with smaller harmonic cores (Sellwood 1981), although something else can happen (see Section 5.2.3) if the core is very small or absent.
Because it grows through swing-amplification, this mode is highly
unstable in massive disks with low velocity dispersion, whenever the
feedback loop is open. If the disk is massive enough to contribute
most of the central attraction, then 1
 X
X
 3 for m = 2
disturbances (Eq. 19), and strong amplification occurs
unless Q
3 for m = 2
disturbances (Eq. 19), and strong amplification occurs
unless Q  2.
2.
In mass distributions with quasiharmonic cores, i.e. those that allow
ingoing waves to reflect off the center, the instability can be
quelled either by a high degree of random motion
(Athanassoula &
Sellwood 1986)
or by making the disk unresponsive to m = 2 disturbances, by
making X
 3 (Eq. 19). This
latter solution is that favored by
Ostriker & Peebles
(1973),
Efstathiou et
al. (1982),
and by
Christodoulou et
al. (1995)
who correctly
argue that bar stability can be achieved if a large fraction of the
central attraction over most of the inner disk comes from unresponsive
spherically distributed matter (bulge and halo). However, this is not
the only, or even the most realistic, way to stabilize a dynamically
cool disk.
3 (Eq. 19). This
latter solution is that favored by
Ostriker & Peebles
(1973),
Efstathiou et
al. (1982),
and by
Christodoulou et
al. (1995)
who correctly
argue that bar stability can be achieved if a large fraction of the
central attraction over most of the inner disk comes from unresponsive
spherically distributed matter (bulge and halo). However, this is not
the only, or even the most realistic, way to stabilize a dynamically
cool disk.
After having elucidated the mode mechanism, Toomre (1981) predicted that the formation of a bar could be prevented if the in-going m = 2 wave were unable to reflect off the center of the disk. The easiest way to prevent feedback through the center is to ensure that the wave encounters an ILR, where it will be absorbed as illustrated in Fig. 2.
Simulations of models with centers dense enough to force an ILR for most patterns (Sellwood 1985; Sellwood & Moore 1999; Sellwood & Evans 2001) confirm that Toomre's proposed mechanism can indeed stabilize a disk in high-quality numerical work. These globally stable galaxy models have massive disks with realistic rotation curves and a moderate degree of random motion.
5.2.3. Bar formation through nonlinear trapping
However, Efstathiou et al. (1982) reported that bars formed in their simulations with equal vigor no matter how dense they made the central bulge, in apparent contradiction with Toomre's prediction. Sellwood (1989b) confirmed that bars formed in his similar simulations with dense bulges when the initial arrangement of the particles was random. But he also found that the same models did not form bars when the particles were uniformly spaced in azimuth around rings to reduce the initial level of shot noise in the low-order sectoral harmonics – a quiet start. This different behavior arose because the absorption of in-going spiral waves at an ILR is predicted to occur at small amplitudes only. The higher level of shot noise from randomly placed particles seeds larger amplitude disturbances that can overwhelm the ability of the ILR to absorb them. The resulting non-linear trapping of particles causes a bar to form that is superficially similar to that formed through the global linear instability. Had Efstathiou et al. (1982) employed a much larger number of particles, a less subtle way to beat down the level of shot noise, they should have found that dense bulges can indeed stabilize a disk, as Toomre predicted. Thus the bulge and halo masses required by the popular stability criteria proposed by Ostriker & Peebles (1973), Efstathiou et al. (1982) and Christodoulou et al. (1995) simply do not apply to galaxies with dense centers, or to high-quality simulations of models with this property.
Shot noise from the ~ 1010 disk stars in real galaxies must have a low amplitude. Larger density fluctuations caused by star clusters and GMCs still seem unlikely to trigger nonlinear bar formation. However, this nonlinear method of making bars in globally stable disks could still occur, for example, by a large amplitude perturbation caused by a tidal encounter or minor merger (see Section 5.2.5).
5.2.4. Slow trapping of orbits
Lynden-Bell (1979), in an elegant piece of dynamical analysis, proposed a mechanism for the secular growth of bars in galaxies. He showed that eccentric stellar orbits could, under certain reasonable conditions, gradually become trapped into a rather slowly rotating bar structure. Orbits tend to align in the inner parts of galaxies, thereby reinforcing the bar, when the overall density distribution is not too sharply peaked toward the center. Lynden-Bell (1979) envisaged that the angular momentum loss from the inner part of the galaxy would be mediated by spiral patterns, as may have happened in the simulations of (James & Sellwood 1978). This mechanism can be important for the secular growth of bars discussed below (Section 5.3).
Even though the mechanism was originally envisaged as a slow trapping process, Polyachenko (2004, 2013) argued it may also form slow bars on a dynamical timescale. He argued that this was the cause of the weak, slow bars that formed in the simulations described in the appendix of Athanassoula & Sellwood (1986), which had velocity distributions that were strongly radially biased. The mechanism has also been identified (Palmer et al. 1990) as the root cause of the radial orbit instability in spheroidal stellar systems with radially biased DFs.
5.2.5. Bar formation through tidal encounters
A number of studies of tidal interactions of satellite galaxies with disks have shown that bars are often triggered by the encounter (Byrd et al. 1986; Noguchi 1987; Gerin et al. 1990; 1991Salo ; Mayer & Wadsley 2004; Romano-Dáaz et al. 2008b). If the unperturbed disk were stable, bar formation could still occur through the nonlinear trapping mechanism described in Section 5.2.3.
Miwa & Noguchi
(1998)
suggest that tidally induced bars might be slower, in the
sense that  ≫ 1, than
those formed through the usual bar instability.
Curir et al.
(2006)
also report that bars seemed to form more
readily in cosmologically formed halos with moving substructures than
in cases where the halo is smooth and nonevolving.
Berentzen et
al. (2007)
reported that interacting galaxy models with large gas fractions
appeared to be less susceptible to bar formation than their gas-free
counterparts, although the high numerical viscosity of the SPH method
(Section 5.5) may have had an undue influence on this
conclusion. The variety of possible galaxy mass ratios, orbits, spin
directions, gas fractions, etc., implies that the comparatively few
simulations so far reported have barely scratched the surface of this
vast multidimensional, parameter space.
≫ 1, than
those formed through the usual bar instability.
Curir et al.
(2006)
also report that bars seemed to form more
readily in cosmologically formed halos with moving substructures than
in cases where the halo is smooth and nonevolving.
Berentzen et
al. (2007)
reported that interacting galaxy models with large gas fractions
appeared to be less susceptible to bar formation than their gas-free
counterparts, although the high numerical viscosity of the SPH method
(Section 5.5) may have had an undue influence on this
conclusion. The variety of possible galaxy mass ratios, orbits, spin
directions, gas fractions, etc., implies that the comparatively few
simulations so far reported have barely scratched the surface of this
vast multidimensional, parameter space.
Despite a number of studies to attempt to determine whether galaxies with nearby companions or those in dense environments are more likely to be barred, the results have generally been inconclusive. Skibba et al. (2012) review this work, and present a much larger study of their own, based on barred classifications from the Galaxy Zoo project, that appears to find a significant excess of bars in galaxies with moderately distant companions. Much more theoretical work and further observational studies (e.g. Méndez-Abreu et al. 2012) are required to determine the extent to which bars in real galaxies could be caused by interactions.
The changes to the distribution of both mass and angular momentum that result from this global instability are the largest that occur in an isolated disk (Hohl 1971; Debattista et al. 2006). However, for reasons given below, bar formation through a global instability is widely believed to happen just once in the life of most disk galaxies, and the associated large structural changes are not expected to recur.
Bournaud & Combes (2002) and Combes (2008) offer a dissenting view, and found that the instability can recur in their simulations. The process of bar formation and dissolution (Section 5.6) creates much random motion, leaving the original stellar disk dynamically "hot" and unresponsive. However, gas settling onto circular orbits and forming new stars creates a new, dynamically responsive, component. Thus, they invoke a high gas accretion rate in order that the whole disk may again become bar unstable. Some of their simulations did form a second bar, in Bournaud & Combes (2002) after the disk mass had roughly doubled, and Sellwood & Moore (1999) presented an additional case.
However, it is hard to see how such behavior could recur repeatedly, since each cycle adds mass to the hot unresponsive disk population. Also, angular momentum changes associated with earlier bar formation will have made the disk more centrally concentrated, which is stabilizing as Sellwood & Moore (1999) demonstrated. Furthermore, inside-out disk growth suggests that fresh gas is expected to be accreted less in the center, where it would most be needed, and more in the outer disk.
A globally unstable bar-forming mode generally has an open spiral form, which causes a large-scale rearrangement of the angular momentum in the disk. However, the spiral soon fades, leaving the bar as the only persistent feature and the outer disk dynamically much hotter. If the disk does not extend far beyond the bar, and the simulation does not include a live halo or any dissipative component, then very little further happens.
A more extended disk can support continuing spiral activity for a period, which generally has a lower pattern speed than that of the bar (Sellwood & Sparke 1988), and the duration of that activity can be extended, perhaps indefinitely, by mimicking dissipation. The apparent connection between the bar and the spiral pattern in such cases must be transitory, although Sellwood & Sparke (1988) showed that contours of the nonaxisymmetric density distribution appear to join the bar to the spiral for a significant fraction of the beat period. Whether spirals in real barred galaxies are driven responses to the bar or distinct dynamical entities has proven harder to establish (Buta et al. 2009; Meidt et al. 2009).
Although spiral patterns in simulations generally have different
pattern speeds from that of the bar, the two nonaxisymmetric
structures do interact. Generally, it is found that spiral activity
is associated with bar growth, since spirals remove angular momentum
from particles, allowing them to become trapped into the bar
(Lynden-Bell 1979;
Sellwood 1981;
Solway et al.
2012).
This process causes the bar to slow as it grows, because it adds
material to the bar that has a lower natural precession rate (see
Section 5.1), and the
requirement  > 1
continues to hold. Note that spirals do
not always cause bars to strengthen and can sometimes cause them to
weaken, as described in Section 5.6.
> 1
continues to hold. Note that spirals do
not always cause bars to strengthen and can sometimes cause them to
weaken, as described in Section 5.6.
Tagger et al. 1987 and Masset & Tagger 1997 argue that bars can drive spirals through nonlinear resonance coupling. In their picture, the location of corotation of the bar coincides with the ILR of the outer m = 2 spiral, which has a lower pattern speed, and the coupling is mediated by a third mode, which may be axisymmetric (m = 0) or m = 4. Similar ideas were proposed by Fuchs et al. (2005). There is no doubt that many spirals in simulations have pattern speeds of approximately the angular frequency for this to be a possible explanation, but the evidence for the third mode that would confirm it has proved more elusive.
Bars also grow in length due to dynamical friction with the halo (Section 6), and growth by this process can be extreme (Athanassoula & Misiriotis 2002; Martinez-Valpuesta et al. 2006; Villa-Vargas et al. 2009). Athanassoula & Misiriotis 2002 show that a bar in a moderately dense halo continues to grow until it is as large as the disk from which it formed! Perhaps the mechanism proposed by Lynden-Bell (1979) operates in this context also, with secular bar growth caused by loss of angular momentum to the halo instead of to the outer disk. Of course, the bar slows as it grows in these cases also. Since we do not observe bars of this size, in relation to their disks (e.g. Erwin 2005), it seems reasonable to conclude that halo friction, which is determined by the inner halo density (Section 6), is too mild for excessive bar growth to occur in nature.
After a bar has formed and settled, it generally experiences a second instability that causes it to thicken out of the plane into a pronounced peanut shape, as first reported by Combes & Sanders (1981). Combes et al. (1990) and Pfenniger & Friedli (1991) suggested that thickening is caused by a vertical resonance, since gradual thickening also occurs in simulations in which the buckling mode is suppressed by forcing vertical symmetry of the potential about the midplane, but Friedli & Pfenniger (1994) concede that thickening is more rapid when buckling is allowed. The asymmetric bending of the bar when viewed edge-on in many simulations (Raha et al. 1991; O'Neill & Dubinski 2003; Martinez-Valpuesta & Shlosman 2004; Martinez-Valpuesta et al. 2006) is a clear indication that a dynamical buckling instability is the principal cause of the peanut-like shape. The buckling instability of a bar is believed to have formed the peanut shape of the Milky Way bulge (e.g. Shen et al. 2010; Li & Shen 2012; Gerhard & Martinez-Valpuesta 2012), and additional kinematic data (Vásquez et al. 2013) seem to support this picture.
Buckling instabilities had been predicted for a stellar system with an
excessively flattened velocity dispersion ellipsoid
(Toomre 1966;
Kulsrud et
al. 1971;
Fridman &
Polyachenko 1984).
Araki 1985]
showed that the
instability is present in a uniform stellar sheet with a
sech2(z / z0) vertical profile
provided  z <
0.3
z <
0.3 x, and
this criterion appeared to be roughly correct in a global axisymmetric model
(Sellwood 1996).
Simulations of the
nonlinear evolution of the instability in strongly prolate systems
(Merritt &
Hernquist 1991),
disks
(Sellwood &
Merritt 1994),
and the rotating bars of interest
here, reveal that the flattened system develops an increasing bend in
the vertical direction until self-gravity is no longer able to confine
the particles to the bending layer; the nonlinear evolution is a
puffier system with less extreme velocity anisotropy. In the case of
rotating bars, the disk in which the bar formed may have been quite
stable to buckling when axisymmetric, but the formation of the bar
creates an elliptical flow, with substantial streaming motion in the
radial direction that has the same destabilizing effect on the bending
dynamics as does random motion.
x, and
this criterion appeared to be roughly correct in a global axisymmetric model
(Sellwood 1996).
Simulations of the
nonlinear evolution of the instability in strongly prolate systems
(Merritt &
Hernquist 1991),
disks
(Sellwood &
Merritt 1994),
and the rotating bars of interest
here, reveal that the flattened system develops an increasing bend in
the vertical direction until self-gravity is no longer able to confine
the particles to the bending layer; the nonlinear evolution is a
puffier system with less extreme velocity anisotropy. In the case of
rotating bars, the disk in which the bar formed may have been quite
stable to buckling when axisymmetric, but the formation of the bar
creates an elliptical flow, with substantial streaming motion in the
radial direction that has the same destabilizing effect on the bending
dynamics as does random motion.
It is clear that the 2:2:1 resonant orbit family invoked by Pfenniger & Friedli (1991) is the reason that the bar takes on a peanut shape. Orbits of this family dominate in rapidly rotating 3D bars (e.g. Pfenniger & Friedli 1991; Martinez-Valpuesta et al. 2006); in the rotating frame, they close after two radial oscillations (as do the x1 family in 2D) and two vertical oscillations, with the vertical excursions peaking when the particle is far from the center.
The buckling instability weakens the bar (Raha et al. 1991; Martinez-Valpuesta & Shlosman 2004; Debattista et al. 2004, 2006), and causes it to become slightly more centrally concentrated, as energy added to the vertical motions is removed from the horizontal. The peanut shape of the bar after the instability may also be affected by the degree concentration of the central mass: the central waist is more pronounced in models with a quasiuniform inner density distribution, while the thickness is more uniform when the central density is strongly peaked (Berentzen et al. 2007).
The peanut shape generally does not encompass the full extent of the bar, i.e. there is some flat bar outside the buckled inner part (Lütticke et al. 2000; Athanassoula 2005; Gadotti et al. 2007; Erwin & Debattista 2013), as has also been claimed for the Milky Way (Martinez-Valpuesta & Gerhard 2011), with the "long bar" seen in counts of the mid-IR sources (Benjamin et al. 2005) and variable stars (González-Fernández et al. 2012). Erwin & Debattista (2013) also argue that not every bar thickens vertically and estimated that at least 13% of bars in galaxies have not buckled.
Unfortunately, the nature of the buckling instability in simulations depends on spatial resolution (or the gravity softening length) used in the N-body code. Codes, such as that used by Raha et al. (1991), which do not have many zones or softening lengths within the vertical thickness of the disk yield restoring forces to the midplane that are not as sharp as they should be. A soggy restoring force increases the spatial scale of the instability, leading to the simple low-order buckling mode reported by Raha et al. (1991). Subsequent models with better spatial resolution found that bars still thicken, but the buckling occurs on shorter length scales, causing less pronounced bends before the mode saturates.
The inclusion of a rigid mass component, especially a bulge or central mass concentration that is held fixed, also compromises the proper representation of the buckling instability. Such models provide an additional restoring force to the fixed center, whereas a fully mobile mass distribution should move in response to the bend in the thin component (Berentzen et al. 2007).
Martinez-Valpuesta et al. (2006) show that a bar that grows substantially in length may undergo a second buckling instability. Athanassoula & Misiriotis (2002) also found that the extent of peanut appearance grew significantly as the size of bar continued to increase.
5.5. Gas response to bar forcing
As described in Section 2.11, the interstellar medium (ISM) in galaxies is not a simple fluid with a well-defined equation of state. Thus before running simulations to model the gas flow, one must first decide how best to approximate the dynamical behavior of the ISM.
One approach (e.g. van Albada & Roberts 1981; Piner et al. 1995; Kim et al. 2012) is to use a standard Eulerian hydrodynamic code with an isothermal equation of state, adopting a sound speed that is representative of the velocity spread of the clouds, typically between 5 and 10 km s-1 rather than the much lower thermal speed. These well-developed methods have the advantages of optional adaptive grid refinement (e.g. Kravtsov et al. 2002) and a low numerical viscosity, but they also attribute a pressure that resists compression in a converging flow where the physical properties of the gas suggest that we should expect strong dissipation through some kind of bulk viscosity.
Lagrangian methods have also been applied, the most popular of which is smooth particle hydrodynamics (hereafter SPH, see Springel 2010a for a review). The advantage of these methods is that they concentrate numerical resources in the interesting regions of high density, and self-gravity of the gas can readily be combined with the scheme used for the stellar particles. A known weakness of SPH is its inability to support some standard fluid instabilities, especially the Kelvin-Helmholtz instability (Agertz et al. 2007), but fix-ups have been developed (Read & Hayfield 2012; Hopkins 2013). Another weakness of all Lagrangian methods, such as "sticky" particle and "colliding" particle schemes as well as SPH, is the high numerical viscosity due to the finite radius (or kernel width) of the particles. This is of particular importance in spatially separated, but nearby counter streaming flows, such as can occur in strongly nonaxisymmetric potentials. Two nearby streams of oppositely flowing particles whose interpolation kernels overlap will clearly drag on each other, causing viscous dissipation that may be greatly over-estimated.
Springel (2010b) described a promising new hybrid Eulerian-Lagrangian method that adjusts the grid cell boundaries as the fluid flows. However, the number of published examples is so far rather small, and most are applied to galaxy formation, rather than to galaxy evolution.
Since no one method perfectly mimics the dynamics of the ISM, it is good to compare the behavior in any one problem using a variety of techniques. One has greater confidence in behavior that is reproducible by more than a single method.
5.5.1. Flows in two dimensions
Many have reported simulations of a massless gas component flowing in a rigidly-rotating bar potential (a partial list of some the more important papers is: Sanders & Huntley 1976; Sanders & Tubbs 1980; Matsuda & Isaka 1980; Schwarz 1981; van Albada & Roberts 1981; Athanassoula 1992; Kim et al. 2012). These simulations used a variety of approximations to model the gas, but generally they found that gas within the bar region is driven inward toward the galaxy center, where it accumulates, while gas in the region outside corotation is driven outward.
Because the gas is moving highly supersonically, pressure is negligible and, except where shocks arise, the motion of a fluid element follows a ballistic orbit. Therefore, were shocks absent, mild dissipation would drive gas onto streamlines corresponding to periodic orbits in the potential. However, in most bar flows, the periodic orbits do not nest without intersecting others or themselves, as exemplified in Fig. 11, and shocks must form. Shocks form along the leading edges of the bar as it rotates, causing the gas to lose both energy and angular momentum. The loss of angular momentum occurs because the shocks skew the flow pattern with respect to the axis of the bar, and therefore the gas spends more than half its time on the leading side of the bar, where the nonaxisymmetric part of the bar potential applies a retarding acceleration. In all models except those that lack a central mass concentration, the inflow stalls at some distance from the center, which happens where the x2 orbit family appears.
Observational evidence from barred galaxies (reviewed in Kormendy & Kennicutt 2004) suggests that something like the behavior just described also happens in nature. Prendergast (1962) appears to have been the first to associate shocks with the dust lanes that are generally seen on the leading edges of the bar, assuming the outer spiral to trail. Physically, a shock in simulations of the idealized ISM implies, in real galaxies, locations where streams of gas clouds undergo more frequent collisions, causing a change in momentum, and a large increase in density that gives rise to the dust lane. Steep velocity gradients across dust lanes can be detected in high resolution velocity maps (e.g. Weiner et al. 2001; Hernandez et al. 2005; Zánmar Sánchez et al. 2008) and massive gas concentrations are observed in the centers of barred galaxies (Sheth et al. 2005; Regan et al. 2006; Gerin et al. 1988; Garcia-Barreto et al. 1991a). Large accumulations of gas, presumably having been driven inwards by the bar, are often found in circumnuclear rings (Garcia-Barreto et al. 1991b) (see Section 7.1).
Extracting a reliable estimate of the inflow rate of gas from simulations is fraught with difficulties, however. The high numerical viscosity of some methods may enhance the inflow rate (Prendergast 1983) but, even more insidious, is that the precise position of the shock, and therefore the magnitude of the gravity torque on the gas, is strongly affected by the choice of numerical scheme and parameters. Quillen et al. (1995) imaginatively took an observational approach to avoid these pitfalls, although other difficulties arise associated with accounting for all phases of the gas.
A small fraction of the radial flow may continue inward (Wada 2004; Kim et al. 2012), perhaps driven by weak spirals that are particularly prominent in dust (Carollo et al. 1998; Martini et al. 2003). Again, the inflow rate in a simulation depends strongly on the numerical scheme and parameters Kim et al. (2012) and Kim & Stone (2012) found that including magnetohydrodynamics substantially increases the inflow rate in this region. However, it is clear from the observed build up of gas in the nuclear rings of real barred galaxies, that the inward mass flux interior to the ring must be lower than that which flows down the bar into the ring.
Wada & Koda (2001) included self-gravity of the gas, as well as heating and cooling. But the more important limitation of most simulations mentioned in this section is the neglect of the bar response to the angular momentum gained or lost by the gas and the evolution of the gravitational potential as mass accumulates in the center.
Most 3D studies of gas flows in bars have employed the SPH method with an isothermal equation of state. Since there are few results from other 3D methods with which to compare, it makes sense to compare with the 2D behavior, especially as no dramatically new features have been reported that arise specifically from the freedom of motion in 3D. Indeed, Pérez (2008) showed that the flow velocities obtained by SPH compared well with those from a 2D Eulerian method.
Another feature of added realism in most studies is that the self-gravitating evolution of the SPH particles is combined with that of stellar particles (e.g. Berentzen et al. 1998; Fux 1999). This aspect therefore implies that the simulations capture both the angular momentum loss to the bar, and the changing gravitational potential as the gas accumulates in the center. However, while the flow patterns are broadly similar to those seen in 2D models, a characteristic new feature of many of these Lagrangian models is a high inflow rate of isothermal gas to the center. 9 This finding raises a concern that the quantitative inflow rate may be substantially over-estimated because of the numerical viscosity inherent in the SPH method. An artifact of this kind will cause gas to accumulate in the center too quickly, and the effects of the central mass build-up, especially in gas-rich models, may occur too rapidly. Note that this concern is not over the physical process, which surely does happen, but over the rate at which it happens in the simulations.
Berentzen et
al. (2007)
found that the build-up of a central mass concentration
due to gas inflow caused a slight increase in the bar pattern speed,
probably because the increased mass in the center raises orbit
frequencies. They also found a reduced slow-down rate of the bar,
since the bar must take up the angular momentum lost by the gas as it
is driven inwards. Another finding was that a significant gas
fraction altered the buckling behavior, which changed the final
strength and 3D shape of the bar. In a follow-up study,
Villa-Vargas et
al. (2010)
found that moderate fractions of gas
( 5% of the disk mass)
have little effect on the behavior; the bar grew, slowed and buckled
pretty much as in a comparison stars only case.
5% of the disk mass)
have little effect on the behavior; the bar grew, slowed and buckled
pretty much as in a comparison stars only case.
Bars in N-body simulations that do not include any dissipative component or a live halo are long-lived structures (Miller & Smith 1979) that are also quite robust (Sparke & Sellwood 1987). But it has long been recognized (e.g. Pfenniger & Norman 1990) that the build-up of a central mass concentration (CMC) at the center of the bar can change its dynamical structure. Studies to determine the response of a bar to an imposed central mass (Norman et al. 1996; Shen & Sellwood 2004; Athanassoula et al. 2005; Debattista et al. 2006) have generally found that the bar is weakened, but not completely destroyed by a central mass as large as a few percent of the disk mass, and still larger masses are needed to cause the bar to dissolve entirely. The destructive power of a given mass is also increased by making it more dense. Note that a high central density requires that simulation particle orbits near the center have short time steps (Shen & Sellwood 2004), and numerical errors in this regime can accelerate bar dissolution.
The CMC alters the gravitational potential of the bar, which in turn requires the orbital structure to adjust. Shen & Sellwood (2004) found that the massive compact CMC in their model made large parts of phase space chaotic, 10 causing an abrupt dissolution of the bar. Lower mass CMCs also caused some orbits to become chaotic, weakening the bar after which the weakened bar continued to adjust more gradually toward a new structure in the presence of the CMC.
A complete dissolution of the bar leaves the disk dynamically hot, since the highly eccentric orbits of the bar no longer remain aligned in a coherent streaming flow, but become randomly oriented. The process can be very rapid because of collective effects; the coherent alignment of the bar orbits is maintained by the bar potential and, as the bar weakens, the orbits of remaining stars are less strongly constrained to precess at the original common rate. Since the bar has usually buckled by this time, the hot inner disk formed this way is also quite thick. Finally, a very dense central mass can scatter orbits in any direction, and the stars could take up a spheroidal shape, perhaps flattened slightly by the potential of the surrounding disk (Norman et al. 1996). There should be observable consequences from this sequence of events that could test the predictions of the simulations.
Bournaud et al. (2005) and Combes (2008), who use sticky particles to mimic gas, claim that the back reaction of the torque between the bar and the gas can be strong enough to dissolve the bar. They correctly point out that gas inflow must add angular momentum to the bar which should weaken it (Lynden-Bell & Kalnajs 1972). However, the angular momentum required to dissolve the bar should be at least roughly equal to that it lost to the outer disk when it was formed, perhaps more if the bar has been intensified through spiral activity or halo friction (Section 5.3). Thus gas inflow through the comparatively small lever arm of the bar, in comparison to the outer disk, would indeed need to be prodigious to supply the angular momentum to unbind the bar. Berentzen et al. (2007), for example, did find that the bar weakened earlier as the gas mass fraction was increased, but they argued this behavior was caused by the accumulation of mass into the center rather than a back-reaction of the torque between the bar and the gas.
A third possible internal method to weaken a bar is an interaction with an exceptionally strong spiral, which has occurred in a few simulations (e.g. Sellwood & Moore 1999, Solway et al. 2012). Lynden-Bell & Kalnajs (1972) derived Eq. (20) by averaging over all phases, which they assumed to be uniformly populated, leading them to the widely cited conclusion that spirals remove angular momentum from the inner disk. However, the stars are far from uniformly distributed in azimuth near the end of a bar and the fact that they are trapped in the bar further invalidates, in this context, the assumptions that underlie the derivation of Eq. (20). The behavior in this more complex situation seems to depend on the relative phase of the spiral arm and the bar. For most of the cases when the bar leads, or is close to the same phase, as the inner end of the spiral, the spiral can remove angular momentum from nonbar stars which may allow them to become trapped into the bar, thereby increasing the bar strength, as described in Section 5.3. On the other hand, when the spiral density maximum significantly leads the bar, their mutual attraction adds angular momentum to stars in the bar, which weakens it. This behavior has not been studied in detail, and further work is required to understand it and quantify its likelihood.
All three bar weakening mechanisms are discussed further in Section 8.
5.7. Discussion of bar fraction
None of the proposed methods to form bars, or of preventing their formation, seems able to give a convincing explanation for the observed fraction of bars in galaxies. Furthermore, Bosma 1996, Courteau et al. 2003, and others have pointed out that barred galaxies seem little different from their unbarred cousins in most respects – e.g. they lie on the same Tully-Fisher relation. Sánchez-Janssen & Gadotti (2013) did find significant differences between barred and unbarred galaxies in photometric parameters, which they attribute to evolution caused by the bar.
Barazza et al. (2008) report an anticorrelation of bar frequency with the bulge light fraction and Buta et al. (2010a) found a decreased frequency of strong bars in S0 galaxies, which have dense and massive bulges. Both these studies offer weak support for the stabilizing mechanism proposed by Toomre (1981). But this cannot be the whole story because some near-bulgeless disks lack a strong bar (e.g. M33) while other barred disks have massive bulges.
The inability of theory or data to find a clear predictor for the incidence of a bar in a particular galaxy suggests that whether a particular galaxy is or is not barred may depend on unobservable factors such as its formation history (see also Sheth et al. 2012).
Erwin (2005, see also Hoyle et al. 2011) found that bars in early-type galaxies are larger than those in late-type galaxies, both in absolute size and in terms of the scale length of the disk light. He also noted that bars in many real galaxies, especially of late Hubble type, are shorter than those in simulations, which is another reason to think that our understanding of bar formation in real galaxies remains incomplete.
Tremaine & Weinberg (1984a) devised a method to measure the pattern speed of a bar directly from observations of a tracer component, which must obey the equation of continuity. Their original method assumes that the galaxy has but a single pattern, and would yield a misleading result were there more than one pattern, each rotating at a different angular rate.
The stellar light distribution of early-type barred galaxies is
believed to obey the equation of continuity because these galaxies
have little dust obscuration and no star formation. They also rarely
possess prominent spirals in the outer disk. Results of many studies
using this method for early-type barred galaxies were summarized by
Corsini (2008).
While some individual measurements are quite
uncertain, the data seem to favor 1 <

 1.4.
(Chemin &
Hernandez 2009)
found a counter-example in a low-luminosity galaxy.
1.4.
(Chemin &
Hernandez 2009)
found a counter-example in a low-luminosity galaxy.
Fathi et al. (2009) and Meidt et al. (2009) applied the method of Tremaine & Weinberg (1984a) to ionized and to molecular gas, respectively. Both groups argue that this is valid, even though the separate gas components do not obey the continuity equation that underlies the method. Fathi et al. (2009) generally found fast bars. Meidt et al. (2008) generalized the method to attempt to measure radial variations in the pattern speed and Meidt et al. (2009) found suggestions of pattern speeds that are lower at large radii than those near the center.
Other methods can yield indirect estimates of bar pattern speeds.
Fits of models of the gas flow (Section 5.5) have
been reported for a few galaxies
(Lindblad et
al. 1996;
Weiner et al.
2001;
Pérez et
al. 2004;
Zánmar
Sánchez et al. 2008),
finding  ~ 1.2 in all cases.
Athanassoula (1992)
argued that the shapes and locations of dust lanes in
bars also seem to suggest that
~ 1.2 in all cases.
Athanassoula (1992)
argued that the shapes and locations of dust lanes in
bars also seem to suggest that

 1.2. If the 4:1
resonant orbit family (dotted curves in
Fig. 11) gives
rise to the "boxy" appearance of a bar, then that bar must be fast,
as the orbit family cannot be populated in slow bars. Identifying a
ring in a barred galaxy as the location of a major resonance with the bar
(Buta & Combes
1996)
yields, with kinematic information, an estimate of the pattern speed.
1.2. If the 4:1
resonant orbit family (dotted curves in
Fig. 11) gives
rise to the "boxy" appearance of a bar, then that bar must be fast,
as the orbit family cannot be populated in slow bars. Identifying a
ring in a barred galaxy as the location of a major resonance with the bar
(Buta & Combes
1996)
yields, with kinematic information, an estimate of the pattern speed.
Rautiainen et
al. (2008)
computed models of the stellar and gas (using sticky
particles) responses to forcing by photometric models of 38 barred
galaxies, in which they assumed that the entire nonaxisymmetric
structure rotated at the same pattern speed. They attempted to match
the model to the visual morphology of the galaxy, and found a range of
values for  . However, in
most cases where
. However, in
most cases where  ≫
1, the fit is dominated by the outer spiral, which may have a lower
angular speed than does the bar.
≫
1, the fit is dominated by the outer spiral, which may have a lower
angular speed than does the bar.
The nuclear regions of many barred galaxies show isophote twists (e.g. Shaw et al. 1993) that are interpreted as inner secondary bars within large-scale primary bars. Erwin & Sparke (2002) identified secondary bars in > 25% of barred galaxies and reported that they have a length some ~ 12% of that of the primary bar. The deprojected angles between the principal axes of the two bars appeared to be randomly distributed, suggesting that the two bars may tumble at differing rates. This inference was supported by Corsini et al. (2003), who used the Tremaine & Weinberg (1984a) method to show that the two bars in NGC 2950 could not have the same rotation rates; Maciejewski (2006) used the same data to argue that the secondary bar has a large retrograde pattern speed. Fathi et al. (2007) infer an angular speed for the secondary bar that is higher than that of the primary in NGC 6946.
The theoretical challenge presented by these facts is substantial, and progress toward understanding the dynamics has been slow. Maciejewski & Sparke (2000) studied the orbital structure in a potential containing two nonaxisymmetric components rotating at differing rates. However, a self-consistent secondary bar can neither rotate at a uniform rate (Louis & Gerhard 1988) nor can it maintain the same shape at all relative phases to the primary.
Friedli & Martinet (1993) argued that gas was essential to forming secondary bars (see also e.g. Heller et al. 2001; Englmaier & Shlosman 2004). However, some of the collisionless simulations reported by Rautiainen & Salo (1999) and Rautiainen et al. (2002) manifested dynamically decoupled inner structures when the inner disk had high orbital frequencies due to a dense bulge. The structure was more spiral-like in some models, but others appeared to show inner bars that rotated more rapidly than the main bar.
Debattista & Shen (2007) created long-lived, double-barred galaxy models in collisionless N-body simulations having dense inner disks, which they described as pseudobulges. They followed up with a more detailed study (Shen & Debattista 2009) that also made some predictions for observational tests. The secondary bars in their models indeed rotated at nonuniform rates, with a shape that also varied systematically with phase relative to that of the primary.
These models prove that purely collisionless dynamical systems can support this behavior. However, it remains unclear what initial conditions have given rise to double-barred galaxies in nature.
The possible consequence of gas inflow in these galaxies has attracted a lot of attention. Shlosman et al. (1989) speculated that bars within bars might lead to gas inflow over a wide range of scales, from global to the parsec scale where accretion onto a black hole might cause AGN activity. While inflows may have been observed (e.g. Haan et al. 2009; van de Ven & Fathi 2010), understanding of gas flow in these nonsteady potentials remains rather preliminary (Maciejewski et al. 2002; Heller et al. 2007).
Many papers (a partial list is: Knapen et al. 2000; Laine et al. 2002; Laurikainen et al. 2004; Hao et al. 2009; Lee et al. 2012) have discussed the vexing question of whether there is, or is not, an excess of active galactic nuclei (AGN) in barred galaxies. Even the observational question is hard to answer, because a low level of AGN activity can be confused by a high rate of star formation, and low-ionization nuclear emission regions (LINERs). It is also necessary to ensure that the barred and unbarred galaxy samples to be compared have similar distributions of luminosities, colors, etc.
Emphatically one can answer that a single large-scale bar in a galaxy
cannot drive gas close enough to the black hole to be accreted, and
therefore produce an enhanced level of activity. Torques on the gas
from the bar are able to reduce its angular momentum by about a single
order of magnitude, leaving it orbiting the nucleus at speeds
 100 km s-1 at a distance
100 km s-1 at a distance
 200 pc. Its angular
momentum must be reduced by at least a further 2 orders of magnitude
before the gas could join even the dusty torus that is thought to
surround the accretion disk in a typical AGN
(Krolik 1999).
Thus the essence of the debate is whether secondary (or even multiple) bars,
nuclear spirals, magnetic fields, etc. can bridge this gap and
deliver to the accretion disk some of the larger supply of
circum-nuclear gas that resides in barred galaxies.
200 pc. Its angular
momentum must be reduced by at least a further 2 orders of magnitude
before the gas could join even the dusty torus that is thought to
surround the accretion disk in a typical AGN
(Krolik 1999).
Thus the essence of the debate is whether secondary (or even multiple) bars,
nuclear spirals, magnetic fields, etc. can bridge this gap and
deliver to the accretion disk some of the larger supply of
circum-nuclear gas that resides in barred galaxies.
Since the argument over the observational evidence continues, with perhaps the nay sayers in the ascendant at the present time, one concludes that there is no clear, direct connection between large-scale bar inflow and AGN activity, and there may be none at all.
8 Although the instantaneous angular momentum of an individual particle in a strongly nonaxisymmetric system changes continuously, particles in a settled bar stream round the bar in a steady fashion such that the distribution of their instantaneous values does not evolve. Back.
9 Debattista et al. (2006) found reduced inflow with an adiabatic equation of state because the gas is then more resistant to compression. However, the pressure of even an isothermal gas may be unrealistic (see Section 2.11). Back.
10 Gerhard & Binney (1985) predicted this consequence for nonrotating ellipsoidal galaxies. Back.