1. INTRODUCTION

Shortly after the discovery of quasars at great cosmological distances (Schmidt 1963), it was realized that the energy required to power these luminous and compact sources must be of gravitational origin rather than from nuclear reaction (e.g., Hoyle & Fowler 1963, Salpeter 1964, Zel'dovich & Novikov 1964, Lynden-Bell 1969). The standard picture now is that mass is accreted onto a supermassive black hole (SMBH) at the center of the galaxy, and the gravitational energy is released during this accretion process to power quasar activity. If the SMBH grows mostly via this accretion process, its mass growth rate is simply: _BH = L_Edd(1 - є) / (є c²), where L_Edd = lM_BH = 1.26 × 10³⁸(M_BH / M) erg s^-1 is the Eddington luminosity of the BH, = L_bol / L_Edd is the Eddington ratio, and є is the radiative efficiency, i.e., the fraction of accreted rest mass energy converted into radiation. If both and є are non-evolving, the BH mass increases by one e-fold on a characteristic timescale t_e ≡ є c² / [(1 - є) l] 4.5 × 10⁸ є / (1 - є) yr, also known as the Salpeter time or e-folding time. If quasars do not radiate beyond the Eddington limit = 1, the observed luminosity provides a lower-limit on their BH mass (e.g., Zel'dovich & Novikov 1964). The discovery of luminous quasars (with L_bol 10⁴⁷ erg s^-1) at z > 6 (e.g., Fan et al. 2001, Mortlock et al. 2011) then suggests that SMBHs with M_BH > 10⁹ M are already formed in the first billion year after the Big Bang.

In the past two decades or so, there has been tremendous progress in the demographic studies of SMBHs in the nuclei of nearby galaxies (for recent reviews, see, e.g., Kormendy & Richstone 1995, Ferrarese & Ford 2005, Kormendy & Ho 2013). It has come to the consensus that SMBHs with masses of ~ 10⁵-10¹⁰ M are almost ubiquitous at the center of massive galaxies with a significant spheroidal (bulge) component, and also exist in at least some low-mass galaxies. More remarkably, the mass of the nuclear BH is tightly correlated with the properties of the bulge in the local samples (e.g., Gebhardt et al. 2000, Ferrarese & Merritt 2000, Graham et al. 2001, Tremaine et al. 2002, Marconi & Hunt 2003, Aller & Richstone 2007, Gültekin et al. 2009), allowing an estimate of the local SMBH mass function by convolutions with galaxy bulge distribution functions. These BH-bulge scaling relations promoted the notion of BH-galaxy co-evolution, during which the energy release from the accreting SMBH self-regulates its growth, and impacts the formation and evolution of the bulge via feedback processes (e.g., Silk & Rees 1998, King 2003, Di Matteo et al. 2005). Such feedback from active SMBHs (i.e., AGN feedback) has also been invoked in most present-day theoretical modeling of galaxy formation, to bring better agreement with the observed statistics of massive galaxies. However, the significance of AGN feedback and BH-host co-evolution is still under some debate and is an active area of research.

An elegant argument tying the local relic SMBH population to the past active population is the Sotan argument (Soltan 1982): if SMBHs grow mainly through a luminous (or obscured) quasar phase, then the accreted luminosity density of quasars to z = 0, _•,acc, should equal the local relic BH mass density _•:

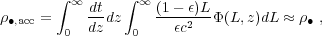(1)

where (L,z) is the bolometric luminosity function (LF) per L interval. Given the observed quasar luminosity function, a reasonably good match between _•,acc and _• can be achieved if the average radiative efficiency є ~ 0.1 (e.g., Yu & Tremaine 3112002, Shankar et al. 2004, Marconi et al. 2004, also see Salucci et al. 1999; Fabian 1999; Elvis et al. 2002), consistent with the mean є value constrained from individual quasars with spectral fitting (e.g., Davis & Laor 2011). The Sotan argument and its variants have been used extensively in recent years to model the growth of SMBHs with constraints from the demographies of local BH relics and the past AGN population (for a recent review, see Shankar 2009). These exercises are mainly facilitated by the advent of modern large-scale, multiwavelength sky surveys, which have provided large and homogeneous data sets many folds more than what was available twenty years ago, as well as measurements of the abundance and clustering properties of quasars with unprecedented precision.

The growth of SMBHs is among the key science topics in modern galaxy formation studies (for a relatively complete summary of recent progress on this topic, see, e.g., Alexander & Hickox 2012 and references therein). As one of the few fundamental quantities describing a BH, the mass of quasars is of paramount importance to essentially all quasar-related science: the evolution and phenomenology of quasars, accretion physics, the relations and interplays between SMBHs and their host galaxies.

In this review I discuss the current status of quasar BH mass estimations and how these developments can further our understandings of the physics and evolution of SMBHs. I presume the reader has a basic understanding of AGNs and I will skip elaborations on the usual AGN terminologies, which can be found in AGN textbooks (e.g., Peterson 1997, Krolik 1999). This review is mostly pragmatic without going into the detailed and sometimes poorly understood physics behind observations; some further readings can be found in the quoted references.

There are several recent reviews on measuring active and inactive BH masses (e.g., Peterson 2010, Czerny & Nikolajuk 2010, Vestergaard et al. 2011, Marziani & Sulentic 2012), which summarized some general concepts and practical procedures in measuring SMBH masses. While some of the common materials are also covered in the current review for completeness, the scope and focus of this review are different: after an introduction on BH mass measurements in Section 2, I describe in detail the caveats and statistical biases of the most frequently used BH mass estimators in Section 3, in light of recent work invoking statistical quasar samples; several applications of these BH mass estimates to quasar studies are discussed in Section 4, and I conclude this review in Section 5 with a discussion on future perspectives of improving BH weighing methods. A flat CDM cosmology is adopted throughout this review, with = 0.7, ₀ = 0.3 and H₀ = 70 km s^-1 Mpc^-1.