The aim of these lectures is to review the main aspects of secular galaxy evolution, i.e., galaxy evolution on cosmological scales. Two issues stand out in this attempt. First, the subject is immense and cannot be covered within the scope of this chapter. And second, one cannot ignore the fact that galaxy evolution is part of the overall evolution in the Universe - from the largest spatial scales ruled by dark matter (DM) to the smallest ones taken over by dissipative baryons that can form stars and grow supermassive black holes (SMBHs). In other words, the process of galaxy formation can be influenced strongly by a huge range of spatial scales. Hence, our attempt to discuss secular galaxy evolution will be rather modest in depth, only highlighting those issues which appear to lie at the forefront of current research. Lastly, we shall focus on disk galaxy evolution and only briefly mention elliptical galaxies.
Galactic morphology is largely a reflection of underlying dynamical and secular processes on relevant scales. That morphological evolution does indeed take place has been established fairly well, e.g., a recent quantitative analysis comparing galaxy populations at redshifts z ~ 0.6 and z = 0 (Delgado-Serrano et al. 2010). While the fraction of ellipticals has barely changed over the last ~ 5 Gyr, the fraction of peculiar galaxies grew in favour of spirals by a factor of ~ 2-3. So peculiar morphology increases dramatically with z (e.g., Brinchmann & Ellis 2000).
As the galaxy population does indeed exhibit evolutionary trends, the question is what drives this process and how can we analyse and quantify it. Overall, our goal lies in explaining the origin of the contemporary Hubble sequence and in describing changes in this sequence over z. In this context, two alternative views exist. Firstly, the Hubble fork is determined by the initial conditions, i.e., by Nature. That means, for example, that the massive galaxies form in the highest overdensities, which themselves resulted from initial conditions. Alternatively, it is the environment, i.e., Nurture, not Nature, that determines the galaxy properties. Within this framework, evolution is driven solely by interactions, e.g., between galaxies, between galaxies and the intergalactic medium (IGM), etc.
In the past couple of decades, the issue of structure formation in the Universe, in terms of the dichotomy of top-to-bottom versus bottom-up scenarios, has been resolved in favour of the latter, and of the cold dark matter (CDM) paradigm. Unfortunately, even within the bottom-up framework, it remains unclear when and where the baryons matter. Clearly, on large scales the baryons follow the DM. But where and when do the baryons run amok 1? Inside the DM haloes? In the cold filaments? As the baryons collapse into the haloes, where do stars form - in disks or spheroids? Is gas fragmentation encouraged or suppressed during this infall? To what degree is the angular momentum conserved during collapse?
These questions open a Pandora's box of dissipative baryon dynamics partially decoupled from the DM. They underline pressing problems of structure formation on galactic and subgalactic scales. Most importantly, they emphasise the old/new dichotomy of what is primarily responsible for disk evolution: internal or external factors. Keeping this in mind, it is possible to construct a follow-up list of outstanding problems according to anyone's taste. Why do disks form inside triaxial haloes? (The haloes appear universally triaxial in numerical simulations, e.g., review by Shlosman 2008.) What is the prevailing morphology of the early galaxies: disk, elliptical, or some other unspecified morphology? Can archaeology help to uncover the details of disk formation and evolution? Important issues here are: can disks survive the epoch of major mergers? and do geometrically thick disks come from mergers or from supernova (SN) feedback?
A separate set of problems is related to disk-halo dynamical and secular interactions, which can have profound effects on both components - a kind of a dynamical feedback. To what extent does the disk evolution at high z differ from that at low z? What is the origin of bulges and galactic bars? And what does this tell us about internally versus externally-driven disk evolution?
Beyond star formation, what is the role of baryons in disk evolution? What are the dynamical corollaries of gas presence, e.g., in maintaining the disk spiral structure? More specifically, does the gas (and the baryon fraction) vary systematically with the halo mass, Mh? When do baryons form central SMBHs? Does feedback from stellar and SMBH evolution encourage or suppress further star formation?
Finally, are disk galaxies doomed, in the sense that ultimately they will fall into high-density regions, and what does that tell us about the morphology-density relation at high z? When did the current morphology-density relation form, and what regulates star formation in disks, stellar mass loss or cold infall?
Much of the theoretical progress understanding the drivers of galaxy evolution is due to numerical simulations of collisionless and dissipative processes in the Universe. Over the last few decades, astronomy has acquired precious support from an experiment, albeit a virtual one. Because the dominant processes are so nonlinear, the synthesis of theoretical, observational and experimental components has contributed much of our current understanding of structure formation in the Universe on all spatial scales. If our goal is to be able to `produce' realistic galaxies that can be directly compared with observations, we are well underway.
The challenges in understanding galaxy formation and evolution are amplified by the unknown physics of the dominant processes (e.g., star formation, mechanical and radiative physics, turbulence), supplemented by often counter-intuitive nonlinear dynamics and by insufficient observational constraints. The numerical approach also suffers from the large dynamic range to be addressed by simulations - from ~ 10-100 Mpc down to ~ AU. Gravity is the source of this difficulty.
The cornerstone of the current galaxy formation paradigm was established and refined in 1970s-1990s. It has been very successful in predicting and explaining disk galaxy properties. A two-stage process has been suggested, based on hierarchical clustering and DM halo formation in the first stage, and gas cooling and collapse into pre-existing potential wells in the second one (e.g., White & Rees 1978; Fall & Efstathiou 1980; Mo et al. 1998). Prior to gravitational collapse, the DM haloes acquire angular momentum (J) via gravitational torques, while baryons follow the DM and have the same specific angular momentum, j = J / M. In the next step, while the DM `warms' up during virialisation, the baryons can cool down and continue the collapse, with j, and hence its distribution, roughly constant. Finally, the low-j baryons accrete onto the inner regions and cause central starbursts, resulting in the formation of galactic bulges in disk galaxies and SMBHs in their centres. Meanwhile high-j baryons form galactic disks with self-regulated star formation. In this framework, j determines the disk size, and the disk surface density fixes the timescale for star formation.
Another milestone has been passed with the understanding that pure DM
structure formation leads to a universal density profile in virialised
objects (e.g.,
Navarro et al.
1996,
hereafter NFW). This density
profile has been approximated by a power law with a slope of -2
(in log 
-
log R) at some characteristic radius
Rs. It becomes shallower and tends to a slope
of -1 toward the centre, and steepens to a slope of -3 at
large radii. Over a range of radii, the NFW density profile leads to a
flat circular velocity curve. The dissipative baryon influx into the
halo is accompanied by a substantial adiabatic contraction of the
non-dissipative DM in the central region, which is being dragged in,
modifying the mass distribution there (e.g.,
Blumenthal et al.
1986).
The adiabatic contraction of the DM halo has been invoked in
order to explain the `conspiracy' of so-called maximum disks (e.g.,
Burstein & Rubin
1985).
However, additional processes that may have
been omitted in the original estimate of the adiabatic contraction can
complicate this picture quite substantially (e.g.,
Primack 2009).
This galaxy formation paradigm has received substantial support from both observations and high-resolution numerical simulations, although a long list of caveats exists. The theoretical background for DM mass and angular momentum distributions is still unclear and remains at the forefront of astrophysical research.
In this conjecture, the value of the angular momentum, its distribution and conservation, emerge as one of the dominant parameters, if not the dominant one determining galaxy evolution, along with the halo mass. To understand the caveats associated with J, we define the dimensionless angular momentum parameter which characterises the DM haloes (e.g., Bullock et al. 2001):
 |
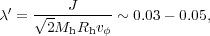(1) |
where Mh and Rh are the halo's
virial mass and radius, respectively, and
v
is its circular velocity. Numerical simulations
point to the universality of the
' log-normal distribution
 |
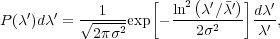(2) |
where ' = 0.035
± 0.005 is the best-fit value, and
(') ~ 0.5 is the width of
the log-normal distribution.
Equation 1 is a slightly modified version of the original spin
parameter introduced by
Peebles (1969),
with ~ 0.01-0.1 being
the range found for DM haloes, and its median
~ 0.035. The simple
relation between and
'
is given by ' =
|ESIS /
ENFW|1/2, where ESIS and ENFW
are the energies of isothermal and NFW haloes.
The collapsing baryons will be stopped by the centrifugal barrier if
J is conserved. In the absence of DM,
' ~ (Rd
/ Rh)1/2, where Rd is the
radius of a disk embedded in the halo. To reach rotational support,
' must increase by a
factor of ten, to
' ~ 0.5. This means
that a collapse will proceed over two
decades in R and the resulting Rd /
Rh ~ 0.01 will be uncomfortably small. On the other
hand, baryon collapse within a DM halo leads
to ' ~
Rd / Rh. This
requires only a collapse by a factor of 10 in R in order to be in
agreement with observations, resulting in Rd ~ 8
(' /
0.035)(H0 /
Hz)(v / 200 km s-1) kpc (e.g.,
Mo et al. 1998).
Here H0 and Hz are the Hubble
constants at z = 0 and at an arbitrary redshift, and
v is the maximum rotational velocity in the disk
(which is also the halo circular velocity for maximum disks). The
corollaries are that, e.g., haloes with higher
' lead to lower
surface brightness disks, and that the resulting disk size distribution
originates in the '
distribution.
However, the observed spread in Rd appears to be
larger than the spread in
' (e.g.,
de Jong & Lacey
2000).
Furthermore, an analysis of the
Courteau (1997)
sample of local massive disks has shown that gas may lose some of its
angular momentum
(Burkert et al.
2009).
Comparison of these disks
with the half-light radii of z ~ 2 SINS galaxies (e.g.,
Förster-Schreiber
et al. 2009;
Cresci et al.
2009),
reveals a similar deficiency of the spin parameter for the latter. We
return to this issue in Section 2. While
the above discrepancies must be clarified, a
number of other caveats threatening the current paradigm require much more
serious attention, and will be discussed below.
1 From the Malay meaning `mad with uncontrollable rage'. Back.