2. DISK GROWTH: THE ANGULAR MOMENTUM PROBLEM

Within the galaxy formation paradigm of White & Rees (1978) and Fall & Efstathiou (1980), the DM haloes acquire their spin from tidal interactions and baryons increase their rotational support by falling into the potential wells of these haloes and by conserving their angular momentum. To what degree the baryon angular momentum is preserved during this process has emerged as one of the key issues in our understanding of disk galaxy formation.

2.1. The angular momentum catastrophe

So is there a problem with J when forming galactic disks? We start with the so-called angular momentum `catastrophe' which has emerged from the comparison of observations with numerical simulations of disk formation. While the observed disks have shown a deficiency of specific angular momentum j by a factor of two, modelled disks appear to have radial scalelengths smaller by a factor of 10 compared with observations, resembling bulges rather than disks (e.g., Navarro & Steinmetz 2000). In other words, the actual disks rotate too fast for a given luminosity L. At the same time, the slopes of the modelled disks turned out to be in agreement with the I-band Tully-Fisher (TF) relation for late-type galaxies, L ~ v_max, where ~ 2.5-4, increasing to ~ 3 in I. In our context, this is important because TF defines the relation between the dynamical mass and L. Simulations have shown much more compact endproducts of baryonic collapse, where the gas has lost a substantial fraction of its j. As we shall see below, the possible remedy to this problem involves a combination of numerical and physical factors, but no universal solution has been found so far.

What are the possible contributors to the angular momentum catastrophe? The first suspect is lack of numerical resolution. Indeed, increasing the resolution by adding smooth particle hydrodynamics (SPH) particles (e.g., Lucy 1977; Monaghan 1982) has improved the situation by helping to resolve the maxima of rotation curves, resulting in flatter and lower curves, thus having an effect on the central and outer regions of modelled galaxies (e.g., Governato et al. 2004; Naab et al. 2007; Mayer et al. 2008).

Numerical non-conservation of j is another suspect. In the outer disks, it can cause an excess of angular momentum transfer to the halo (e.g., Okamoto et al. 2005). In the inner disks, this effect could smear the radial gradients of rotation velocity, and artificially stabilise the disks against bar instability. Modelling an isolated galaxy formed from a non-cosmological Milky Way-type DM halo has demonstrated that low-resolution disks heat up and lose j to the halo. Colder disks remain larger and have smaller bulge-to-disk ratios. A possible solution lies in the increase of the number of SPH particles and the introduction of a multi-phase interstellar medium (ISM).

Next, the disk ISM cooling below the Toomre (1964) threshold of Q c_s / G = 1 leads to an excessive fragmentation (we return to this problem when discussing over-cooling). Here c_s is the sound speed in the gas, - the epicyclic frequency, and - the disk (gas) surface density. The multi-phase ISM introduced by Springel & Hernquist (2003) through a modified equation of state clearly alleviated the problem. The gas cooling must be compensated by some kind of feedback to avoid fragmentation and the follow-up runaway star formation. This feedback from stellar evolution, e.g., from SNe and OB stars, has a clear effect on the bulge-to-disk ratio (Robertson et al. 2004; Heller et al. 2007b).

Finally, it was pointed out that baryons can hitchhike inside DM halo substructures which spiral in to the centre as a result of dynamical friction (e.g., Maller & Dekel 2002). This process is similar to that in a disk, where in the absence of star formation, dense gas clumps would heat up the disk, spiral in to the centre and possibly contribute to the bulge growth (e.g., Shlosman & Noguchi 1993; Noguchi 1999; Bournaud et al. 2007). This process, related to overcooling, can be easily over- or underestimated because it depends on a number of additional processes, e.g., gas-to-stars conversion, ablation, etc. (see Section 6.1). Also, one cannot neglect the contribution of clumpy DM and baryons to the mechanical feedback (i.e., by dynamical friction), and, consequently, to the fate of the central DM cusp and the formation of a flat density core in the halo (e.g., El-Zant et al. 2001; Tonini et al. 2006; Romano-Díaz et al. 2008a).

2.2. The cosmological spin distribution and individual haloes

We now turn to the distribution of angular momentum in DM haloes. Early considerations of the baryon collapse assumed an initial solid-body rotation for uniform-density gas spheres. The angular momentum distribution (AMD) can be written as M(< j) = M_h[1 - (1 - j / j_max)^3/2], where j_max is some maximum j, if baryons preserve j during this process, which results in exponential disks (e.g., Mestel 1963). More generally, what is the shape of an AMD which leads to exponential disks? The initial solid-body rotation law is soon replaced, following assumptions that baryons are mixed well with the DM and share its j. Assuming j conservation, M_d(< j) / M_d = M_h(< j) / M_h, where M_d is the disk mass (e.g., Fall & Efstathiou 1980; Bullock et al. 2001; Maller & Dekel 2002), the new AMD can be written as

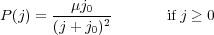(3)

and P(j) = 0 if j < 0. This leads to a mass distribution with j

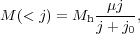(4)

with two parameters, µ - the shape, and j₀ = (µ - 1) j_max - whose effect on M(< j) has been displayed in Bullock et al. (2001, Fig. 4) for four haloes. When using the best-fit j₀, and normalising by M_h, all haloes follow the same curve nicely - an indication of the universality of the AMD. The resulting (computed) disk surface density is nearly exponential, but with an over-dense core and an overextended tail.

Using Swaters' (1999) sample of 14 dwarf disk galaxies, van den Bosch et al. (2001) have demonstrated that the specific AMDs (i.e., M(< j)) of these disks differ from halo AMDs proposed by Bullock et al. (2001). But the total disk j's, i.e., P(), are similar to those of haloes. Although the pre-collapse baryon and DM AMDs are expected to be similar, the disks formed have been found to lack low and high j - in direct contradiction to the simple theoretical expectations discussed above. Moreover, the mass fraction of Swaters' disks appears to be significantly smaller than the universal baryon fraction in a CDM universe. Does this mean that disks form from a small fraction of baryons and, in spite of this, attract most of the available angular momentum? One can argue that a redistribution of baryon j should occur (at a stage earlier than anticipated), or that the high-j baryons avoid the disks. What processes are responsible for modifying the baryon AMDs? As argued by van den Bosch et al. (2001), a plausible explanation can lie in the selective loss of the low-j gas, leading to essentially bulgeless disks.

The closely-related issue of the existence of bulgeless disk galaxies is discussed in Section 6.

2.3. The tidal torque theory and the origin of the universal angular momentum distribution

Rotation of galaxies results from gravitational torques near the time of the maximum expansion (e.g., Hoyle 1949; Doroshkevich 1970; White 1978). If J is calculated using the spherical shell approximation (i.e., linear tidal torque theory, hereafter TTT) further redistribution during the non-linear stage contributes little (Porciani et al. 2002a, b). Alternatively, J can be acquired in the subsequent non-linear stage of galaxy evolution via mergers, accounting for the orbital angular momentum and its redistribution (e.g., Barnes & Efstathiou 1987).

According to the TTT, J is gained mostly in the linear regime of growing density perturbations due to the tidal torques from neighbouring galaxies. The maximum contribution to J comes from the times of the maximum cosmological expansion of the shell. Little J is exchanged in the non-linear regime after the decoupling and virialisation of the DM. Baryons are well mixed with the DM and acquire similar j (see Section 1). The TTT follows the evolution of the angular momentum of the DM halo based on the moment of inertia tensor and the tidal tensor. Within this framework, galactic spins can be estimated using the quasi-linear theory of gravitational instability. The TTT has been extensively tested by numerical simulations.

So far we have not considered the effect of the mergers on the evolution of J (or ). We define mergers as major if their mass ratio is larger than 1:3. Wechsler (2001) has argued that major mergers dominate the j-balance in galaxies. Do they? The crucial point here is to account for the redistribution of the angular momentum during and after the merger. Hetznecker & Burkert (2006) have separated the main contributors to ~ J|E|^1/2 M^-5/2, i.e., J, E and M_h, and followed them during and after the merger event. While the DM halo J experiences a jump during a major merger, the subsequent mass and energy redistribution in the halo washes out the gain in J. A similar conclusion has been reached by Romano-Díaz et al. (2007) and is displayed in Fig. 1. The corollary of high-resolution DM simulations is that there is no steady increase in the halo cosmological spin with time due to major mergers.

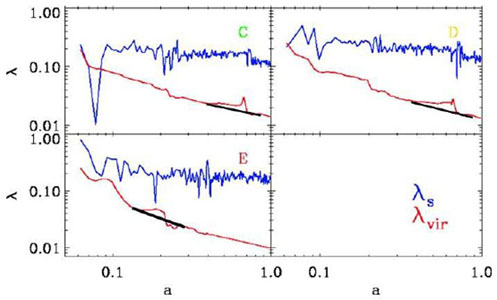Figure 1. Evolution of DM halo spin as a function of a, the cosmological expansion parameter, during major mergers in three models, C-E. In all frames: the blue (upper) curves show the spin s within the characteristic NFW radii. The red (lower) curves show the evolution of the spin vir within the halo virial radii. The thick (black) line has been applied to show the `normal' evolution during major mergers (from Romano-Díaz et al. 2007).