3. DISK GROWTH: MERGERS

In this and the following sections we shall review the details of secular and dynamical growth in disk galaxies which involve merging and/or the accretion of cold gas (Fig. 2). In the simplest (unrealistic) case of an isolated collapsing cloud, the angular momentum is conserved because the escaping radiation is isotropic and carries little J anyway. It is possible that some of the gas will rebound and escape in the equatorial plane taking away some J.

Figure 2. Disk growth mechanisms involve mergers and/or gas accretion. Both options depend on the environment, and their effects are gradually quenched in clusters of galaxies. The dependence on redshift is (1 + z)2 ± 2 for mergers, and seems to have a peak around z ~ 2, but this is yet to be verified for the gas accretion.

The lowest energy state for a rotating self-gravitating cloud occurs when almost all of the mass is found in the central compact accumulation (i.e., SMBH) and a negligible mass and all of the angular momentum escape to infinity. Such a state is never achieved, however, because the efficiency of J-transfer is declines rapidly as the process goes on. Amusingly, to quote Colgate & Petschek (1986), `there seems to be too much angular momentum in the Universe to allow the formation of stars [...]. This fundamental problem begs for solution. Since net J appears to be zero over very large scales [...] our problem is restricted to local patches of the Universe where matter collapses to form relatively dense rotating objects [...].' We note that in order to understand how galaxies grow, one needs to resolve the issue of what is the most efficient angular momentum loss mechanism in particular circumstances.

Disk galaxies form inside DM haloes, and it seems clear that Nature's choice is the formation of self-gravitating disks rather than a complete and efficient collapse to the very centre. Disks can form slowly from a weakly rotating gas cloud, in an adiabatic process, and their properties in this case will be linked to the initial conditions. Or they can form on a short dynamical timescale, forgetting the initial conditions in the process. In such a process, how much J is transferred to the DM and how much is redistributed among the baryons?

What factors affect the secular growth of galactic disks? The following list of physical factors and associated processes was not compiled in order of significance, and are not mutually exclusive:

• Environment: determined by high/low density fields and their corollary - supply of cold gas (from filaments, etc.), major and minor mergers (in the low velocity dispersion field), interactions/harassment (in the high velocity dispersion field), stripping (tidal, ram, strangulation).
• Rate of star formation, feedback from stellar evolution and active galactic nucleus (AGN), galactic winds.
• Intrinsic factors: local and global gravitational instabilities, degree of asymmetry in the host DM halo.

In the following, we shall discuss some of the above factors, but shall avoid going into details about the internal dynamics of stellar bars (see review by Lia Athanassoula, this volume) and general aspects of galactic dynamics (see review by James Binney, this volume). This means that we shall emphasise the external factors driving galaxy evolution, and only occasionally resort to internal factors. Two such exceptions involve the physics of the central kiloparsec and some aspects of the formation of SMBHs (Section 8). We note, however, that this separation is largely artificial, and the action of external triggers of galaxy evolution is frequently associated with `excitation' of internal degrees of freedom. One such well-known example is the tidal triggering of stellar bars.

In order to grow, galaxies and their haloes must rely on the exterior reservoir of baryons and DM, respectively. These can come in various degrees of virialisation: from smooth to clumpy accretion (see Section 5), from carrying nearly unvirialised to fully virialised baryons and embedded in parent DM haloes. The latter lead to mergers of various mass ratios, from major, to intermediate, to minor. The physics of accretion of course differs profoundly depending on the smoothness of accreting material. Mergers can also include stellar and DM components. In the following, we are going to discuss the main processes which accompany merging: dynamical friction, phase mixing and violent relaxation.

Mergers are a diverse phenomenon and their products are equally diverse. We first discuss the criterion for merging, then merger demographics, i.e., their role in forming and growing spheroids and gas-rich disks (wet/dry mergers). We follow this up by reviewing the effect of major mergers on starbursts and AGN, and the effect of minor mergers on disk heating. The relationship between mergers and morphology evolution, stripping, and, briefly, the origin of ellipticals are discussed next. Two questions will be emphasised: whether mergers play an important role in creating spheroids, and whether dry mergers move galaxies along the red sequence.

The process of merging can be defined as an encounter of two galaxies which results in the formation of a single galaxy. Based on the mass ratios of the merging objects, we distinguish between major mergers (> 1:3), intermediate mergers (from 1:3 to 1:10) and minor mergers (< 1:10). Mergers in gas-rich systems are highly dissipative and denoted as `wet' mergers, while mergers in gas-poor systems are dissipationless and `dry'. Finally, mergers can be binary or multiple when more than two galaxies are involved.

Mergers are important because their rate grows rapidly with redshift, (1 + z)^m, although the inferred rate exhibits a substantial scatter. The differences come from matching the rate for rich clusters and for field galaxies, but also because of using different methods, such as close pairs and morphology. Extending the measure to fainter magnitudes generally shows an increase in m. There is also a difference between observational and theoretical estimates. Specifically, m = 6 ± 2 in rich clusters (e.g., van Dokkum et al. 1999), but it is much smaller in the field (m = 2.7 ± 0.6; e.g., Le Fevre et al. 2000). A recent comparison between optical and near-infrared (NIR) bands has revealed a substantial difference in the major merger rate of m = 3.43 ± 0.49 and 2.18 ± 0.18, respectively (Rawat et al. 2008). Diverse observations have resulted in an overall range of m = 2 ± 2, while numerical simulations result in a narrow range of m ~ 3, although ignoring the possibility of multiple galaxies per DM halo.

The situation is more confusing with the redshift dependence of the cold gas accretion rate as few observational constraints exist. On the other hand, numerical estimates of accretion growth are possible. For z 2, accretion rates show a strong increase towards lower z, and a sharp decline thereafter.

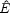
In order to delineate the relevant parameter space for mergers, we define two dimensionless parameters, the energy 2E / ² and the specific angular momentum j / r_m, where is the inner dispersion velocity and r_m is the median (half-mass) radius of an idealised galaxy. With a gross simplification of such spherical, nonrotating equal-mass galaxies it is possible to delineate the - 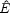parameter space of mergers with a characteristic timescale of less than the Hubble time (Fig. 3). Note that merging can occur also from unbound orbits. As a rule of thumb, only galaxies with relative velocities less than their internal dispersion velocities, v_rel , will merge. Dispersion velocities inside large galaxies are ~ 200-300 km s^-1, while that of clusters of galaxies ~ 500-1000 km s^-1. The merger orbital angular momentum depends on v_rel and contributes to the spin. A simple recipe to increase the parameter space for mergers is the dynamical friction mechanism.

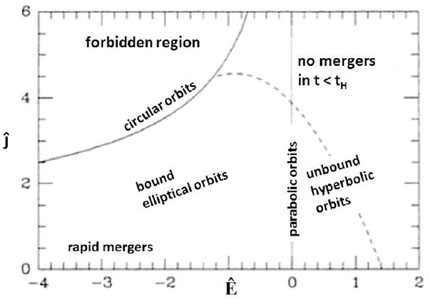Figure 3. Criterion for merging (modified Figure 7-9 from Binney & Tremaine 1987), which is based on the time required for the merging of two galaxies as a function of the initial position of the binary orbit in the - plane. Orbits are only possible outside the forbidden region delineated by the solid lane (circular orbits). All elliptical (bound) and some hyperbolic (unbound) orbits below the dashed lane will eventually lead to a merger. However, merging time increases rapidly toward the upper-right corner, and above the dashed lane the merging time exceeds the Hubble time.

3.1. Mergers and associated processes

3.1.1. Minor mergers and dynamical friction

Minor mergers are those with m ≪ M. When the massive galaxy with mass M moves among the background of low-mass m galaxies (or else) with velocity v, dynamical friction is a good approximation. The drag per unit mass resulting from a gravitational wake is given by (Chandrasekhar 1943)

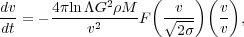(5)

where b_max / max[r_h; GM / v²] is the Coulomb logarithm, b_max is the maximum impact parameter, is the background density of m galaxies, and F is the error function. In the low-v limit, the drag is ~ v, and in the high-v limit, it is ~ v^-2. Also, the dynamical friction force is ~ M², and the DM appears as an important contributor to the friction during the merging process. Assuming a circular orbit with a radius r for M moving around a bound accumulation of m masses, one can arrive at the analytical solution for r(t) which is a linear function of time. However, in a more realistic case, M plunges in a very elongated orbit, with a small pericentre, leading to a substantial tidal disruption and an associated mass loss very early. This of course complicates the analytical solution (e.g., Diemand et al. 2007; Romano-Díaz et al. 2010) and tends to decrease the characteristic timescale for the friction (e.g., Boylan-Kolchin et al. 2008).

The specifics of the dynamical friction are that it is a local and not a global force in the Chandrasekhar approximation, which assumes that the m particles interact only with M. The situation is more complicated if self-gravitational effects are taken into account, which is most relevant for galactic disks. The most interesting corollary is the introduction of resonances between the orbital motion of M and motion of m in the disk, both azimuthal, radial and vertical (e.g., Lynden-Bell & Kalnajs 1972). Other intricacies appear as well, but are not discussed here (e.g., Mo et al. 2010).

The effect of dynamical friction on multiple mergers has been shown explicitly in numerical simulations of Nipoti et al. (2003), who ran them with and without friction with the goal of modelling the formation of cD galaxies in the centres of galaxy clusters. The characteristic timescale for merging has been substantially shortened when the Chandrasekhar drag has acted, compared to merging in a fixed background potential.

3.1.2. Mergers: phase mixing and violent relaxation

The two-body relaxation timescale is too long to have an effect on mergers, where the relaxation is dominated by collisionless processes, such as phase mixing and violent relaxation - relaxation in the mean field. Both mechanisms have been introduced by Lynden-Bell (1967). Behind the idea of phase mixing lies the time evolution of a coarse-grained distribution function in a collisionless system. As the classical entropy is conserved in the absence of collisions, the fine-grained function is time-independent, while the coarse-grained function evolves to uniformly cover the available phase space for the system, thus maximising the corresponding coarse-grained entropy. Phase mixing, therefore, tends to destroy coherent phase-space structure.

Violent relaxation is a relaxation in the time-dependent potential of the system, when the specific energy of a particle is not conserved. This process leads to a Maxwellian distribution of velocities in which the temperature is proportional to the mass of the particle. So particle dispersion velocities become independent of the particle mass. Violent relaxation is most relevant at the time of virialisation of the system, so the characteristic time is the crossing time of the system. This leads to a more complete relaxation in the central regions compared to the outskirts, because the dynamical timescale becomes prohibitively long there. On the other hand, galaxy interactions would drive violent relaxation mostly in the outer regions. It is still unclear how efficient this process is overall.

3.2. Dry and wet disk mergers: spheroids or rebuilding?

Mergers between systems that include stars and DM only are called dry mergers. Examples: a merger of two elliptical galaxies, or one between an elliptical and a lenticular galaxy. Only limited observational data exists on dry mergers, mostly in clusters of galaxies (e.g., van Dokkum et al. 1999). The endproduct of this process is predicted to be an ellipsoidal system (e.g., Toomre & Toomre 1972; Barnes 1992), as inferred from the Sersic law. The mixing appears incomplete, and the metallicity gradient is not fully erased. The emergence of the red sequence of massive galaxies has been linked to the increasing importance of dry mergers after z ~ 1, because of the seemingly insufficient amount of massive blue galaxies that can serve as their precursors (e.g., Khochfar & Burkert 2003; Faber et al. 2007). How important the contribution is of dry mergers in forming the red sequence, however, is unclear.

Dry mergers have been studied using the GEMS (Galaxy Evolution from Morphology and SEDs [Spectral Energy Distributions]) survey in tandem with the COMBO-17 photometric redshift survey in order to constrain their frequency between z ~ 0.2-0.7 (e.g., Bell et al. 2006). Accompanying N-body simulations have been used to explore the morphological signatures of such mergers. An estimated rate of ~ 0.5-2 major mergers between spheroids over the z ~ 0.2-0.7 period has been claimed to be consistent with the limit of 1 such event in recent times, estimated using an alternative semi-analytic method. This indicates that dry mergers can indeed be an important factor in driving the evolution towards massive red galaxies at present times, but more work is clearly required.

Scaling relations, such as Faber-Jackson (1976, FJ), Kormendy (1977), the fundamental plane (Djorgovski & Davis 1987), and others can provide, in principle, important information about the formation of massive ellipticals, and constrain it. N-body simulations have shown that multiple dry mergers preserve the FJ relation, but produce lower central dispersion velocities and increase the effective radius, although the fundamental plane of ellipticals remains thin (Nipoti et al. 2003). Ciotti et al. (2007) confirmed that the FJ, Kormendy and fundamental plane relations are robust against dry merging, although caveats exist. An important question is when are these scaling relations established?

Wet mergers involve gas and are, therefore, dissipative. Here we focus on mergers which involve galactic disks with various gas fractions. When disks are involved, the outcome depends on many more parameters, including the disk plane orientation with respect to the orbital plane, and the alignment of internal spins (rotation) with the orbital spin, i.e., prograde versus retrograde encounters.

The first simulations of disk interactions were performed by Holmberg (1941) using a light-bulb `supercomputer', with the important result that tidal forces lead to the formation of spiral structure in galaxies. Modern numerical simulations have revealed a rich library of processes involving disk interactions and mergers: stretching, harassment, stripping, strangulation, squelching, threshing, splashback and cannibalism. Additional effects include enhanced star formation rates and quenching the star formation (e.g., recall that spheroids are associated with quenched star formation). The outcome of disk galaxy mergers can be either spheroidal or disk systems.

The early arguments about disk merger remnants were based on N-body simulations, without or with low-resolution gas. The merging proceeded via dynamical friction against the DM component. The DM haloes have been `soaking up' the internal and orbital angular momenta of merging galaxies, and the collision appeared sticky (e.g., Hernquist 1992). Overall, the simulations have been successful in fitting the properties of the elliptical products, although the remnants appeared too diffuse compared to observed massive ellipticals. The morphology of interacting and merging galaxies has been closely matched (e.g., Hibbard & Mihos 1995). Dubinski et al. (1996) have studied the merging of pure stellar disks in live DM haloes, focussing on the shapes of tidal tails, when disks are being stretched, imparting kinetic energy to the stars. The length and mass of tidal tails have been found to be sensitive to the gradient of the gravitational potential. Hence, tails can successfully map the DM potential well and constrain the overall DM mass distribution. The problem was in reproducing the high phase density observed in the centres of elliptical galaxies. This situation changed with the inclusion of a dissipative component in simulations.

Numerical simulations have indicated that the dynamical role of gas is well in excess of its mass fraction. This has been shown for isolated galactic models (e.g., Shlosman & Noguchi 1993; Heller & Shlosman 1994) as well as for fully cosmological models (e.g., Barnes & Hernquist 1996). Due to its dissipative nature, gas is always losing its energy and angular momentum, which leads to a central accumulation, where the gas successfully competes with stellar and DM contributions to the gravitational potential. The deepening of the potential well by the gas resolves one of the outstanding issues we have mentioned above - high phase density in the centres of ellipticals. Barnes & Hernquist (1996) have found that the gas presence shortens the merging timescale and drives a large fraction of gas to the very centre of the remnant. This evolution is relatively insensitive to the detailed physics, given that the gas is able to cool. Simulations of mergers involving disks with ~ 10% or less gas mass fraction lead to the formation of a spheroidal stellar component with a surface brightness of the de Vaucouleurs 1/4 law, and a central stellar cusp which is not observed in such galaxies. These simulations have shown that wet mergers can be responsible for the formation of some ellipticals. The question is what fraction?

Difficulties with the scenario of ellipticals forming in binary major mergers of disk galaxies include the following: typical ellipticals are more metal-rich than typical present-day disks (see Fig. 4), ellipticals have older stellar populations that seem to form on shorter timescales, and massive ellipticals could not typically have formed from binary mergers of present day disks (while they might form from high-z disks whose descendants no longer exist (e.g., Naab & Ostriker 2009). In addition, binary mergers of any kind are not isotropic, whereas massive ellipticals are.

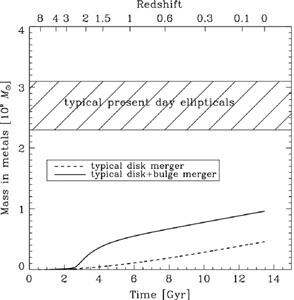Figure 4. Evolution of metals (in mass) for the merger of two M* disks with (solid) and without (dashed) bulge component. The total mass of the progenitor disks used was 2.9 × 1010 M. The metal mass for M* ellipticals is indicated by the shaded area. Present-day ellipticals have (at least) a factor of two more metals (from Naab & Ostriker 2009).

Probably the most intriguing issue of disk mergers is whether disks can survive mergers. Simulations of disk mergers without gas point to a clear trend of mergers thickening and destroying the disks (e.g., Kazantzidis et al. 2008; Robertson & Bullock 2008). The corollary is that the disks must grow rather quiescently. But what about the more relevant situation where disks contain gas, and there are plenty of `leftovers' from mergers? What is the outcome when the disks not only contain gas but are gas-rich? Is there a critical gas fraction, f_gas, for disk survival?

Indications that disks can reform after some major mergers, if sufficient amounts of gas can be maintained, come from simulations of pure-gas, bulgeless disks on prograde parabolic orbits, in the presence of star formation (e.g., Springel & Hernquist 2005). Moreover, gas-rich disks with f_gas 0.5 (e.g., Robertson et al. 2006; Robertson & Bullock 2008), or continuous accretion of the cold gas following a destructive merger (e.g., Steinmetz & Navarro 2002) show a similar trend. Arguments that disk heating has been overestimated in minor mergers have been advanced as well (e.g., Hopkins et al. 2008; Romano-Díaz et al. 2008b). Recent high-resolution simulations of over-dense regions in the Universe have shown a resilient, disk-dominated population of galaxies (Fig. 5) at z ~ 8-10 (Romano-Díaz et al. 2011b). Subsequent analysis of disk growth in such regions reveals that the dominant growth mode is not via major mergers but rather through accretion of cold gas (Romano-Díaz et al. 2012), as we discuss in Sections 5 and 7.

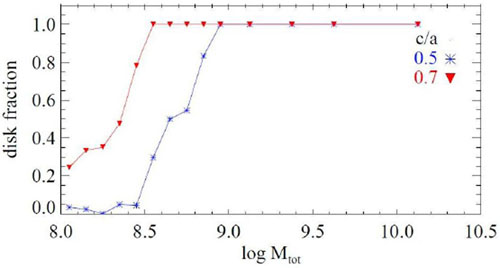Figure 5. Disk fraction as a function of its total (baryon+DM) mass at z ~ 10.2 (in M) within a high-resolution region of 7 h-1 Mpc with binning of 0.25 in total mass. Shown are two defining criteria for the gas disk, c / a 0.5 (blue stars) and c / a 0.7 (red triangles), where a, b and c are the major, intermediate and minor axes of gaseous disks. Haloes in the process of merging have been omitted, overall four objects within this mass range - all of them had more than one disk per halo (from Romano-Díaz et al. 2011b).

Among the few successful examples of an efficient rebuilding of the disk component is a numerical study of disk galaxy evolution following a 1.6:1 wet merger at z ~ 0.8 (Governato et al. 2009). The environment chosen for this experiment was typical of field haloes and Milky Way parameters for the re-simulated galaxy. SN feedback has been responsible for the delayed star formation. For this purpose, the blastwave approximation has been used (see Section 6.2), where the cooling shuts off over a Sedov crossing time of 3 × 10⁷ yr over ~ 0.2-0.4 kpc regions (corresponding also to the resolution limit of the model). During the phase of z < 3, f_gas in the progenitor disks was below 0.25. Over the period of disk rebuilding, ~ few Gyr, the old stellar population, found in the thick disk, has faded considerably. Thus, the formed thin disk dominated the light in the I-band, while the thick disk contributed ~ 70% of the stellar mass, and the stellar halo component faded by z = 0.

A number of corollaries follow attempts to rebuild and sustain disks over cosmological times. First, it apparently requires the existence of a thick stellar disk component, which represents the population of a pre-merger disk. A beautiful example is that of NGC 4762, which exhibits both thin and thick disks (e.g., Burstein 1979). If the thickening has been abrupt, the radial extent of the thick disk provides the size of the original disk at the merger event. The absence of thick disks in some late-type galaxies, e.g., NGC 4244, can be interpreted as a challenge to numerical simulations. It is, therefore, encouraging that Comerón et al. (2011) claim to have identified a sign of the thick disk in this object. On the other hand, it is plausible that in some mergers the stellar disks are destroyed completely.

The other issue lies in the prohibitively long disk-rebuilding timescale at low z, a few Gyr. While this timescale severely limits the number of destructive mergers a galaxy can have at low redshift, z 1, it is unacceptable at high redshift z 6. Simulations show, however, that characteristic timescales for similar processes are substantially shorter at high z, by about a factor of ten, which maintains a robust population of disks even in highly over-dense regions (e.g., Romano-Díaz et al. 2011b; 2012). The morphology-density relation during the epoch of reionisation, therefore, does not follow the trend it exhibits at low z. At what redshifts does this relation take the form of the observed one?

Among the numerous corollaries of disk mergers is their plausible contribution to classical bulges. The observed frequency and mass fraction of classical bulges in disk galaxies are debatable at present, specifically with respect to other bulge types. For example, the origin of so-called disky bulges is unrelated to galaxy interactions, and they result mostly from stellar bar instabilities (e.g., Combes et al. 1990; Pfenniger & Friedli 1991; Raha et al. 1991; Berentzen et al. 1998; Patsis et al. 2002; Martínez-Valpuesta et al. 2006; see also review by Kormendy & Kennicutt 2004). This makes it even more difficult to obtain a quantitative estimate of their link to mergers. On top of this, the merger outcome is sensitive to various associated physical processes and kinematical parameters. As numerical simulations themselves depend on subgrid (and sometimes unknown) physics, attempts have focused on semi-analytical models, although their predictive power has not been verified.

Using observational constraints on disk masses and gas fractions, f_gas, in galaxies, Hopkins et al. (2010) have attempted to predict the properties of merger remnants, and, specifically, to quantify the contribution to classical bulge formation from mergers of various mass ratios. The main result was that major mergers dominate the assembly of L_* bulges, while minor mergers dominate the formation of bulges in low-mass systems. The bulge-to-total mass ratio, B / T, was found to trace the merger mass ratio, µ_gal. A simple correlation, B / T ~ µ_gal(1 - f_gas), has been identified. The straightforward corollary of this correlation is that increasing the gas fraction tends to suppress the bulge formation, which has been interpreted in terms of a reduced efficiency of gas angular momentum loss with increasing f_gas. The by-product of this conclusion is that collisionless systems lose angular momentum more efficiently than dissipative ones, something which is difficult to accept.

As a next logical step, one can ask whether gas-rich high-z disks themselves form in mergers. A sample of such massive, ~ 10¹¹ M, disk galaxies at z ~ 2 has been analysed with SINFONI/VLT integral-field spectroscopy (Genzel et al. 2008). Large random motions have been detected and interpreted in terms of rapid inflows from cold accretion flows which originated in cosmic web filaments (Section 5). Such turbulence can reduce the viscous accretion timescale to below ~ 1 Gyr. The detailed example of the galaxy BzK 15504 at z ~ 2.38 has been studied in sufficient detail by Genzel et al. (2006). This object is characterised by a high star formation rate of ~ 140 M yr^-1, a gas mass of ~ 4 × 10¹⁰ M, and a gas-to-star mass ratio of ~ 0.5. The ratio of circular to dispersion velocity, v / ~ 3, points to a geometrically thick disk, and has been interpreted as the formation stage of the thick galactic disk. Interestingly, BzK 15504 shows no obvious signs of a recent or ongoing merger, e.g., no obvious line-of-sight velocity asymmetry. So, is this object a proto-disk caught in the stage of a rapid but secular evolution? Unfortunately, there is no simple answer to this question. The problem lies in that the same kinematic parameters can also characterise a merger remnant, as shown by Robertson & Bullock (2008).