Copyright © 2013 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2013. 51:393-455
Copyright © 2013 by Annual Reviews. All rights reserved |
The construction of models for simple and composite stellar populations is conceptually straightforward. There are however certain constraints that make the creation of such models rather difficult in practice (incomplete isochrone tables, incomplete empirical stellar libraries, poorly calibrated physics, etc.). In this section the ingredients necessary for constructing model SEDs will be discussed. Areas of particularly large uncertainties will be highlighted, but it is not the goal of this review to provide an exhaustive inter-comparison of various possible model choices. An overview of the entire process of constructing composite stellar populations is given in Figure 1.
2.1. The Simple Stellar Population
The starting point of any SPS model is the simple stellar population (SSP), which describes the evolution in time of the SED of a single, coeval stellar population at a single metallicity and abundance pattern. An SSP therefore requires three basic inputs: stellar evolution theory in the form of isochrones, stellar spectral libraries, and an IMF, each of which may in principle be a function of metallicity and/or elemental abundance pattern. These components are typically combined in the following way:
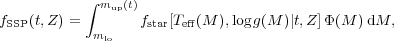 |
(1) |
where M is the initial (zero-age main sequence) stellar mass, Φ(M) is the initial mass function, fstar is a stellar spectrum, and fSSP is the resulting time and metallicity-dependent SSP spectrum. The lower limit of integration, mlo, is typically taken to by the hydrogen burning limit (either 0.08 or 0.1M⊙ depending on the SPS code), and the upper limit is dictated by stellar evolution. The isochrones determine the relation between Teff, log g, and M for a given t and Z. This approach to constructing SSPs is common but not universal. Alternatives include the fuel consumption theorem (Renzini & Buzzoni 1986, Maraston 1998), or the use of empirical spectra of star clusters as templates for SSPs (Bica & Alloin 1986).
Nearly all SPS models provide SSPs as a `black-box' (e.g., Leitherer et al. 1999, Bruzual & Charlot 2003, Maraston 2005, Vazdekis et al. 2010). The user therefore has little working knowledge of how SSPs are built and where major issues lie. The following discussion is therefore largely pedagogical and geared toward users of SPS models, rather than model builders.
2.1.1. Stellar Evolution & Isochrones. An isochrone specifies the location in the Hertzsprung-Russell (HR) diagram of stars with a common age and metallicity. Isochrones are constructed from stellar evolution calculations for stars from the hydrogen burning limit (≈ 0.1 M⊙) to the maximum stellar mass (≈ 100 M⊙). The construction of isochrones is straightforward for stellar evolution tracks that are infinitely well-sampled in mass and time. In practice, evolutionary tracks are discretely sampled and this can lead to issues in isochrone construction for fast evolutionary phases. Modern sets of isochrones have constructed specifically to ensure that the models are relatively immune to these effects (Charlot & Bruzual 1991).
A number of widely-used isochrone tables exist in the literature. The most popular models span a wide range in ages (masses), chemical compositions, and cover most relevant evolutionary phases. Models in this category include the Padova (Bertelli et al. 1994, Girardi et al. 2000, Marigo et al. 2008), and the BaSTI models (Pietrinferni et al. 2004, Cordier et al. 2007). The Geneva models (Schaller et al. 1992, Meynet & Maeder 2000) are tailored to follow high-mass stars through advanced evolutionary phases, including the Wolf-Rayet (WR) phase, but they do not model low mass stars. Other models have focused on the main sequence, red giant branch (RGB), and horizontal branch (HB) evolution of low-mass stars (M < 3 M⊙), including the Y2 models (Yi et al. 2001, Yi, Kim & Demarque 2003), the Dartmouth models (Dotter et al. 2008), and the Victoria-Regina models (Vandenberg & Bell 1985, VandenBerg, Bergbusch & Dowler 2006). Finally, there are isochrones tailored to very low-mass stars and brown dwarfs. The Lyon models are the most widely used in this regime (Chabrier & Baraffe 1997, Baraffe et al. 1998). It is noteworthy that none of the isochrones listed here cover the post-AGB evolutionary phase. Remarkably, the post-AGB isochrones computed by Schoenberner (1983), Vassiliadis & Wood (1994), and Bloecker (1995) are still widely used in modern SPS codes.
Implementing isochrones in an SPS model is challenging because no single set spans the necessary range of ages, metallicities and evolutionary phases. It is common to use the Padova isochrones for the bulk of the age and metallicity range and to supplement with the Geneva models at young ages. Little attention is normally paid to the lowest mass portion of the isochrones, since low mass stars contribute only ~ 1% of the light of an old stellar population. An exception in this regard is the model of Conroy & van Dokkum (2012a), who paid special care to the modeling of low-mass stars for SPS. The splicing together of various isochrone sets can be difficult. For example, different codes make different assumptions regarding convection, rotation, etc., and so the age at which certain stars evolve off the main sequence varies between codes.
Modules for Experiments in Stellar Astrophysics (MESA) is a new, highly modular and sophisticated stellar evolution code that includes the latest stellar interior ingredients including opacity tables, equations of state, nuclear reaction networks, and surface boundary conditions (Paxton et al. 2011). There is great hope that MESA will be employed to produce high-quality isochrones over the full age and metallicity range and for all evolutionary phases.
In addition to the practical difficulty of implementing current isochrone libraries, stellar evolution calculations contain a number of uncertainties relevant to SPS. For example, all of the stellar models mentioned above are based on one dimensional codes. As such, they require approximations to inherently three dimensional processes such as convection, rotation, mass-loss, close binary interactions, and thermal pulses during AGB evolution. These processes lead to major uncertainties in the isochrones that impact the resulting SPS model predictions (e.g., Charlot, Worthey & Bressan 1996, Charlot 1996, Yi 2003, Lee et al. 2007, Conroy, Gunn & White 2009).
The cores of stars more massive than M ~ 1.1 M⊙ are convective, as are the envelopes of evolved giants and low mass stars. Classically, the boundary between convective and radiative regions is specified by the Schwarzschild criterion. However, this criterion is effectively a requirement that the acceleration of a convective fluid element be zero. The fluid element will likely have a non-zero velocity as it crosses this boundary, and so some amount of `overshooting' is expected. This will result in a larger convective region than would be expected from the Schwarzschild criterion alone. With regards to the convective core, a wide body of observational evidence favors the existence of a moderate amount of overshooting in the mass range 1.1 < M / M⊙ < 7 (Stothers 1991, Nordstroem, Andersen & Andersen 1997, VandenBerg & Stetson 2004, Keller & Wood 2006). The amount of core overshooting required to fit the data results in a ~ 25% increase in the main sequence lifetime compared to models that do not include overshooting. Nearly all SPS models adopt isochrones with a modest amount of overshooting in the convective core, as supported by observations. The exception to this is the SPS model of Maraston (1998, 2005), which uses isochrones without core convective overshooting. The treatment of core overshooting has a noticeable effect on the color evolution of SSPs in the age range of ~ 0.1-1 Gyr, by as much as ≈ 0.1 mag (Yi 2003, Conroy & Gunn 2010) and can therefore be an important source of systematic uncertainty when modeling SEDs.
As discussed in Cassisi (2004), the amount of overshooting in the convective envelopes of evolved giants is less constrained. This is unfortunate because the treatment of envelope convection affects, among other observables, the ratio of red to blue helium-burning giants (Renzini et al. 1992). These stars can contribute several tens of percent to the integrated light, depending on the star formation history (Melbourne et al. 2012), and so uncertainty in the amount of envelope overshooting should affect the integrated light predictions at a significant level. Overshooting in the convective envelope also affects the location of the luminosity bump in the RGB luminosity function. This fact was used by Alongi et al. (1991) and more recently by Cassisi et al. (2011) to argue for a modest amount of overshooting in the convective envelope.
The importance of stellar rotation has been investigated by the Geneva group, amongst others, over the past two decades (see Maeder & Meynet 2000, Maeder & Meynet 2012 for a review). Perhaps most importantly, rotation increases the main sequence lifetimes (by ~ 25%) due to rotation-induced mixing bringing fresh fuel to the convective core. Rotation also lowers the effective surface gravity, lowers the opacity in the radiative envelope, increases the luminosity, and changes the ratio of red-to-blue supergiants. The mixing to the surface of H-burning products caused by rotation will also affect the number and type of Wolf-Rayet stars. Vázquez et al. (2007) and Levesque et al. (2012) investigated the impact of rotating massive star models on integrated light properties by comparing to non-rotating models and found that the number of ionizing photons increased by as much as an order of magnitude and colors became bluer by as much as 0.1-1 mag, depending on wavelength and age. The signatures of WR stars as a function of time and metallicity in integrated spectra are also different between rotating and non-rotating models.
Most massive stars are in binary systems, and there is some evidence that massive star binaries preferentially have comparable masses (Kobulnicky & Fryer 2007, Sana & Evans 2011). The interaction of close binary stars via mass-transfer and common envelope evolution will affect the evolution of such stars and bring about further changes to their observable properties. (Eldridge, Izzard & Tout 2008) demonstrated that in many respects the effects of binary star models without rotation are similar to single star models with rotation. Eldridge & Stanway (2012) argued that SPS models including binary star evolution produced a better fit to UV spectra of star-forming galaxies. Regardless of the details, it is clear that where massive stars matter in galaxy SEDs, the effects of both rotation and binary evolution will play an important role. In fact, binary star evolution may also create blue straggler stars and extreme HB stars, which would suggest that binary evolution can affect older stellar populations as well (Han et al. 2002, Han et al. 2003, Zhang et al. 2005). No popular SPS model includes the effects of binary star evolution.
The potential importance of thermally-pulsating AGB (TP-AGB) stars in the context of SPS models was emphasized by Maraston et al. (2006), and has since become a controversial topic. This phase occurs for stars in the mass range ≈ 1 < M / M⊙ < 8 (depending on metallicity) and is difficult to model for several reasons, including the fact that nuclear burning occurs in alternate hydrogen-rich and helium-rich shells. When the helium shell burns it does so explosively because of the thin shell instability (Schwarzschild & Harm 1968), which gives rise to the thermal pulses. Mass-loss becomes catastrophic during this phase, thereby terminating the life of the star. Recently the Padova group has developed a new suite of isochrones with updated TP-AGB models calibrated against observations in the Large Magellanic Cloud (LMC, Marigo & Girardi 2007, Marigo et al. 2008). However, Conroy & Gunn (2010) found that the updated Padova models failed to reproduce the colors of intermediate-age Magellanic Cloud star clusters, by as much as 0.5 mag in some cases. These authors provided recalibrated SPS models in which the weight given to TP-AGB stars was reduced in order to match the LMC data. More recently, Melbourne et al. (2012) analyzed resolved color-magnitude diagrams in nearby dwarf galaxies and concluded that these updated models produce twice as much luminosity in the TP-AGB phase as observed, roughly independent of the inferred mass fraction in young stars. In addition, Melbourne et al. (2012) found that the latest Padova model predictions for the luminosity contributed by red core helium burning stars is a factor of two higher than observed in dwarf galaxies. This problem in the models may be related to the treatment of convection in the envelopes of evolved giants.
Mass-loss is another critical parameter in stellar evolution models. At M ≲ 8 M⊙, it determines when a star will end its life as a white dwarf, and how massive the white dwarf will be. At higher masses mass-loss can significantly alter the course of advanced evolutionary phases, especially at M > 40 M⊙. In high mass stars the mass loss mechanism is thought to be via line-driven winds, while in lower mass stars (≲ 8 M⊙) it is believed to be due to pulsation-induced dust-driven winds (Willson 2000). In any event, the mass-loss prescription is another free parameter in these models, and it is a critical one because it strongly affects the lifetimes of advanced (and luminous) evolutionary phases. For example, the lifetime of TP-AGB stars and the number of thermal pulses they undergo depend strongly on the mass-loss prescription (Ventura & Marigo 2010).
In summary, the computation of isochrones for use in SPS depends on many uncertain aspects of stellar evolution including the treatment of convection, close binary evolution, rotation effects, and mass-loss, amongst many others. The importance of these uncertainties on derived SPS results will be highlighted throughout this review.
2.1.2. Stellar Remnants. Stars eventually die, usually leaving behind stellar remnants in the form of white dwarfs, neutron stars, or black holes (theory predicts that a certain class of very massive metal-poor stars undergoes pair-instability supernovae that leave behind no stellar remnant; Heger et al. 2003). The relation between the initial, zero-age main sequence stellar mass and the final remnant mass is not well-constrained observationally, especially for massive stars. The initial-final mass relation for white dwarfs can be reasonably well constrained by measuring white dwarf masses in open clusters with known ages (e.g., Kalirai et al. 2008). The initial-final mass relation is predicted to be a function of metallicity (Marigo 2001, Heger et al. 2003), further complicating the situation.
In SPS models stellar remnants are usually included in the total stellar mass budget, and their contribution can be significant. For example, if a certain amount of mass is formed into stars instantly, then after 13 Gyr only 60% of the mass remains in stars or stellar remnants; the other 40% has returned to the interstellar medium. Of the remaining stellar mass, 25% is locked in stellar remnants. Of the total remnant mass, 73% is comprised of white dwarfs, 7% is in neutron stars, and 20% is in black holes. These numbers were computed assuming solar metallicity and a Kroupa (2001) IMF, with the initial-final mass relations from Renzini & Ciotti (1993). The Maraston (2005) SPS model predicts similar numbers (largely because the same initial-final mass relation was used). The point is that stellar remnants can make an important contribution to the total stellar mass of a system.
2.1.3. Stellar Spectral Libraries. Stellar spectral libraries are required to convert the outputs of stellar evolution calculations — surface gravities, g, and effective temperatures, Teff — as a function of metallicity, Z, into observable SEDs. There is however no single spectral library, whether theoretical or empirical, that covers the entire range of parameter space necessary for constructing SPS models. Stitching together various libraries, often of widely varying quality, is therefore necessary. Some modelers take the approach of constructing spectral libraries entirely from theoretical calculations, while others use purely empirical libraries. The benefits and drawbacks of these two approaches will be discussed in this section.
2.1.3.1. Theoretical Libraries. Theoretical libraries offer the great advantage of densely covering parameter space, including spectral resolution, and of producing spectra that are not subject to observational issues such as flux calibration and atmospheric absorption. The clear disadvantage is that the libraries are only as good as the input atomic and molecular parameters and the approximations made in the computation of the models, as discussed below.
There are a number of decisions that must be made when computing synthetic spectral libraries including how to treat convection and the microturbulent velocity profile, and whether or not to model departures from LTE and plane-parallel geometries. Additional important limitations include the incomplete and often inaccurate atomic and molecular line lists. As emphasized by Kurucz (2011), models still fail to reproduce all the observed features in ultra high-resolution spectra of the Sun due to incomplete atomic line lists. The situation is even more serious for cooler stars because the molecular line lists can carry fairly large uncertainties, in particular TiO (Allard, Homeier & Freytag 2011). A related problem is that a significant fraction of the atomic and molecular lines are derived from theoretical calculations, rather than measured in the laboratory, and so they have uncertain strengths and central wavelengths. Unfortunately, these `predicted lines' can be important for determining the overall SED shape of stars and hence of galaxies. Worse still, the partition function for many molecules is poorly known, so even the total abundance of particular molecules is uncertain.
The quality and state of the art of the theoretical models varies considerably as a function of Teff. At the high temperature end, i.e., Wolf-Rayet and O-type main sequence stars, the state-of-the-art libraries are from Smith, Norris & Crowther (2002) and Lanz & Hubeny (2003), while for hotter compact objects (e.g., post-AGB stars) the most up-to-date models are from Rauch (2003). By far the widest range in parameter space is covered by the BaSeL atlas (Lejeune, Cuisinier & Buser 1997, 1998, Westera et al. 2002). This library is comprised of a variety of theoretical models from Kurucz (1995), Fluks et al. 1994, Bessell et al. ( 1989, 1991), and Allard & Hauschildt (1995). The broadband SEDs of the stars in this library have been modified to agree with observed UBVRIJHKL color–temperature relations for individual stars. The BaSeL atlas is almost universally used in modern SPS codes, despite the fact that the input theoretical spectra are now almost 20 years old. At the very coolest temperatures the MARCS and NEXTGEN/PHOENIX grids are the state-of-the-art because of their comprehensive molecular line lists and treatment of spherical effects on the atmospheres and spectra of cool giants. Finally, the Aringer et al. (2009) models fill out the low temperature end by providing carbon star spectra over a range of parameter space.
There are several modern spectral libraries computed by Munari et al. (2005), Martins et al. (2005), and Coelho et al. (2005) that offer fairly wide coverage in parameter space and are at high spectral resolution. The Martins et al. (2005) library has even been incorporated into a fully theoretical high resolution SPS model (González Delgado et al. 2005). However, these libraries appear to be geared toward high resolution spectroscopic analyses because they do not include the predicted lines. They therefore cannot be used to model broadband SEDs, or any spectral region that contains a significant contribution from predicted lines. However, progress can be made by making corrections to these high resolution libraries for the effect of predicted lines on the broadband SED, as for example done in Coelho et al. (2007).
2.1.3.2. How Accurate are the Theoretical Libraries? Normally, observed stars are assigned physical parameters based on comparison to models. However, if one wants to constrain the models with observed stellar data then one requires an independent estimate of the physical properties of stars. This is a significant obstacle to assessing the accuracy of the models. One can obtain essentially model-independent estimates of Teff via angular diameter measurements, but these are very difficult to obtain for giants, let alone main sequence stars (Perrin et al. 1998, Boyajian et al. 2012a). A more widely used technique is the infrared flux method (IRFM), first proposed by Blackwell & Shallis (1977). The basic idea is that the flux of a star depends only weakly on Teff in the IR, and so one can deduce angular diameters from fluxes alone with only a weak model dependence. This technique underpins nearly all existing color-Teff relations (e.g., Alonso, Arribas & Martinez-Roger 1996, Ramírez & Meléndez 2005, Casagrande et al. 2010).
The latest generation of model spectra succeed in reproducing the broadband colors for FGK dwarfs and warm giants (Bertone et al. 2004, Kucinskas et al. 2005, Martins & Coelho 2007, Boyajian et al. 2012b). Not surprisingly, the models continue to have difficultly fitting the SEDs of the coolest stars and the flux in the Wien tail of the flux distribution (typically ≲5000 Å for types G and later). The latter difficulty arises because the Wien tail is extremely sensitive to Teff and so even minor changes to the model assumptions lead to large changes in that spectral region. In addition, metal line blanketing becomes very strong in the blue/UV, and so the requirements on the line lists are demanding. Martins & Coelho (2007) explored the ability of three modern synthetic libraries to reproduce a variety of spectral features of observed stars. Overall the agreement was found to be satisfactory, although there were notable deficiencies. Some models were unable to reproduce the observed CH features in cool stars, while other models failed to match the observed Mgb and MgH features. The majority of the model shortcomings were restricted to stars with Teff < 4500 K. Modern models also have difficulty reproducing the strength of the TiO bands in cool stars (Kucinskas et al. 2005, Allard, Homeier & Freytag 2011).
The situation regarding the H2O band strengths in the NIR should serve as a cautionary tale: models have for decades predicted water bands in cool stars that are stronger than observations. Part of the problem seems to have been the molecular line lists, which improved steadily over the years, culminating in the Barber et al. (2006) line list, which contains 500 million transitions. However, Allard, Homeier & Freytag (2011) demonstrated that the recent revision of the solar abundance scale by Asplund et al. (2009), which entails a factor of two reduction in the oxygen abundance, has a much larger effect on the predicted strength of the water bands. Their new models with updated solar abundances reproduce remarkably well the NIR colors of M dwarfs, which have strong water band features. Thus, not only the atomic and molecular parameters but also the abundance patterns can have a very significant effect on theoretical spectra.
2.1.3.3. Empirical Libraries. The strengths and weaknesses of the theoretical libraries are the weaknesses and strengths of the empirical libraries. Empirical spectra of course do not suffer from issues with line lists, treatment of convection, etc., but they are plagued by standard observational constraints such as correction for atmospheric absorption, flux calibration, and limited wavelength coverage and spectral resolution. Worse, the empirical libraries are woefully incomplete in their coverage of parameter space. This is a long-standing issue that is difficult to address owing to the fact that empirical libraries are drawn from samples of stars in the solar neighborhood. For example, hot main sequence stars at low metallicity are very rare, as are stars in rapid phases of stellar evolution such as WR and TP-AGB stars.
One of the first comprehensive empirical stellar spectral libraries was constructed by Gunn & Stryker (1983). Later optical/NIR libraries included Pickles (1998), Jones (1999), ELODIE (Prugniel & Soubiran 2001), STELIB (Le Borgne et al. 2003), Indo-US (Valdes et al. 2004), NGSL (Gregg et al. 2006, Heap & Lindler 2011), MILES (Sánchez-Blázquez et al. 2006), IRTF (Rayner, Cushing & Vacca 2009), and the X-shooter library (Chen et al. 2011). Other, specialized libraries include an ultraviolet atlas compiled from IUE data (Fanelli et al. 1992), a TP-AGB library (Lançon & Mouhcine 2000), and the Spitzer Space Telescope IR stellar library (Ardila et al. 2010). The Sloan Digital Sky Survey (SDSS) has obtained spectra of several hundred thousand stars and has devoted considerable effort to measuring stellar parameters from the spectra (Lee et al. 2008). As yet there is no official stellar spectral library based on the SDSS stars, but it would clearly provide a great leap forward both in terms of coverage in parameter space and uniformity in spectral quality.
An example of the difficulties posed by empirical libraries for SPS model construction is shown in Figure 2. This figure shows the location in the HR diagram of all stars from the MILES spectral library, with stellar parameters determined by Cenarro et al. (2007). MILES is the empirical library today that provides the greatest coverage in terms of log g, Teff, and [Fe/H] with a total of 985 stars. In this figure the metal-rich and metal-poor stars are split into two panels. Overplotted are isochrones from the Padova group for ages ranging from 106.6 - 1010.1 yr. While the lower main sequence and red giant branch are well covered by the empirical library over a wide range in metallicity, hotter stars are rare, especially at lower metallicity. Because the HR diagram is covered so sparsely in this regime, constructing SPS models based on empirical libraries at young ages (≲ 1 Gyr) is clearly challenging.
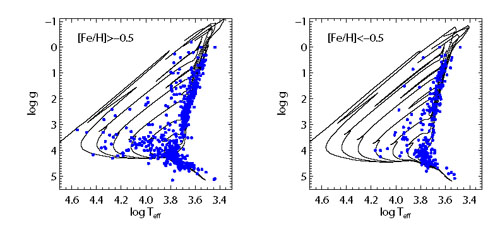 |
Figure 2. Physical properties of the MILES empirical spectral library, separated by [Fe/H] (solid symbols). Isochrones from the Padova group are overplotted for t = 3 × 106 - 1010 yr. Typical errors on Teff and log g are 60-100 K and 0.2 dex, respectively (Cenarro et al. 2007). Notice that the MILES library covers the lower main sequence and RGB both at high and low metallicity, but it only sparsely covers the upper main sequence and supergiants. This figure highlights the difficulty in constructing SPS models based on empirical stellar libraries, especially at low metallicity. |
A second, related problem with empirical libraries is irregular coverage in the HR diagram. Interpolation within the library, necessary for SPS model construction, can be difficult. Vazdekis et al. (2010) has developed a sophisticated algorithm to deal with this issue. These authors assign quality numbers to the resulting SPS models based on the number of empirical spectra comprising each model. This is a profitable approach that should be standard in the field because it allows users to assess the reliability of various regions of parameter space.
A third problem associated with empirical libraries is the assignment of physical parameters to stars, including log g, Teff, and [Fe/H]. Of particular note is the Teff determination, which carries an uncertainty of order 100 K (Alonso, Arribas & Martinez-Roger 1996, Ramírez & Meléndez 2005, Casagrande et al. 2010). Using theoretical models, Percival et al. (2009) explored the impact of uncertainties in Teff, log g, and [Fe/H] for individual stars on SPS models. They found that for models with old ages (> 4 Gyr), the effect of changing the temperature scale by 100 K had significant effects (0.1-0.4 Å in EW in the most extreme cases) on a variety of spectral absorption features, including the hydrogen Balmer lines and several commonly employed iron and magnesium lines used to interpret the stellar populations of early-type galaxies. The work of Percival & Salaris was mostly exploratory, and it would be desirable to consider the full propagation of these sorts of uncertainties into the derived properties of galaxies.
Yet another issue with empirical libraries is the abundance patterns of the stars. It is well-known that low metallicity stars in the Galaxy tend to be α-enhanced, such that [Mg/Fe] ≈ 0.0 at [Fe/H]≈0.0 and [Mg/Fe] ≈ 0.4 at [Fe/H] < -1.0 (Edvardsson et al. 1993). Thus, any model based on empirical stars at low metallicity must somehow correct for this [α/Fe] `bias' in the models (see e.g., Thomas, Maraston & Bender 2003b, Schiavon 2007).
2.1.3.4. Variable Abundance Patterns. Moderate resolution spectra (i.e., R ~ 1000-5000) contain a wealth of information on the detailed abundance patterns of the stellar populations. In the context of SPS models, abundance ratios have historically been estimated through the analysis of spectral indices. Ideally, an index is sensitive to a single feature (such as an atomic absorption line or a molecular band head). One usually defines a feature bandpass and one or two pseudocontinua, and then an equivalent width (EW), or in some cases a magnitude, can be measured. The Lick/IDS system is the most popular index system, defining 21 indices in the wavelength range 4000-6500 Å (Burstein et al. 1984, Worthey et al. 1994). Other index systems have been defined at other wavelengths (e.g., Fanelli et al. 1992, Alvarez et al. 2000, Cenarro et al. 2001, Serven, Worthey & Briley 2005). In practice, the use of indices is greatly complicated by the fact that there are rarely if ever clean regions of the spectrum from which one can estimate the continuum level. The strength of each index thus depends not only on the feature of interest but also the features in the pseudocontinua.
Tripicco & Bell (1995) were the first to assess the sensitivity of the Lick/IDS indices to variation in the abundances of 10 elements with theoretical spectral models. Korn, Maraston & Thomas (2005) provided an update to these `response functions' with updated line lists and transition probabilities, and for a range in metallicity. Serven, Worthey & Briley (2005) considered variation in 23 elements, including several neutron-capture elements. These authors defined new indices sensitive to a host of elements not considered in the earlier work. The Serven models were based on theoretical spectra of only two stars per abundance pattern, a turnoff star and a luminous giant, and the model effectively had a fixed age of ~ 5 Gyr. Lee et al. (2009a) provided response functions for Lick indices by employing a larger number of synthetic spectra. Conroy & van Dokkum (2012a) produced theoretical stellar spectra with variation in 11 elements. These models contained theoretical spectra at 20 points along the isochrone, for ages from 3-13.5 Gyr. Rather than focusing on spectral indices, these models made predictions for the response of the full spectrum from 3500 Å -2.4 μm to abundance variations. Sample response spectra from that work are shown in Figure 3. In this figure the relative response of the spectrum to an increase in the abundance of a particular element is shown. The full spectrum is rich in diagnostic features beyond what any index system can capture.
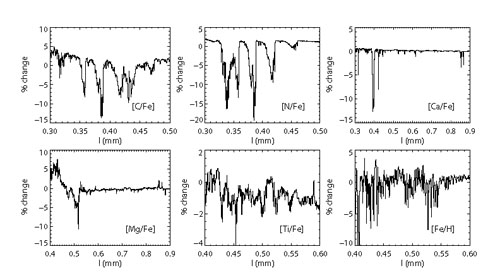 |
Figure 3. Variation in the spectrum of a 13 Gyr SSP due to changes in individual elemental abundances. All abundance changes are +0.3 dex except for C and Ca which are varied by +0.15 dex. Spectra have been broadened to a velocity dispersion of 150 km s-1. Notice the different x and y-axes in each panel. Prominent spectral features include the CH, CN, NH, C2, Ca i, Ca ii H&K, Ca ii triplet, MgH, and Mg b (Mg i) features, along with numerous atomic Fe and Ti features. Computed from the models of Conroy & van Dokkum (2012a). |
To construct models with arbitrary abundance patterns one would want to create synthetic spectra for each possible abundance pattern. When considering large numbers of elements, such an approach becomes computationally infeasible. Instead, the standard technique is to create arbitrary abundance patterns by treating the effect of each element on the spectrum as being independent of the other elements (e.g., Thomas, Maraston & Bender 2003b, Schiavon 2007, Lee et al. 2009a, Conroy & van Dokkum 2012a). This is a reasonable assumption for trace elements, but it is less realistic for elements such as C, N, O, Na, Ti, and Fe, which affect the opacity, free electron density, and/or molecular equilibrium. There has been surprisingly little work in the literature testing this assumption.
2.1.4. The IMF. The initial distribution of stellar masses along the main sequence, known as the stellar initial mass function (IMF), has been studied extensively for decades (e.g., Salpeter 1955, Scalo 1986, Scalo et al. 1998, Kroupa 2001, Chabrier 2003). As emphasized in a recent review by Bastian, Covey & Meyer (2010), there is no compelling evidence for variation in the IMF from direct probes, e.g., star counts. The canonical Salpeter IMF has the form dN / dM ∝ M-x with x = 2.35. The IMF measured in the solar neighborhood deviates from the Salpeter form only at M < 1 M⊙, where x becomes shallower (Kroupa 2001, Chabrier 2003).
From the perspective of SPS, the IMF (1) determines the overall normalization of the stellar mass-to-light ratio, M / L; (2) determines the rate of luminosity evolution for a passively evolving population; (3) affects the SED of composite stellar populations; (4) has a small effect on the shape of the SED of single stellar populations. The last point is due to the fact that the integrated light of a coeval population is overwhelmingly dominated by stars at approximately the same mass, i.e., the turnoff mass. (4) will not hold for IMFs that depart dramatically from the Salpeter IMF. (3) arises because composite populations have a range of turnoff masses that contribute to the integrated light. The fractional contribution of stars of various masses to the total number of stars, stellar mass, and bolometric luminosity is shown in Figure 4. This figure demonstrates quantitatively that low mass stars dominate the stellar mass and number of stars in a galaxy, but contribute only a few percent to the bolometric light of an old stellar population. At younger ages the light contribution from low mass stars is even less.
Tinsley (1980) demonstrated that the evolution in M / L for a passively evolving stellar population is sensitive to the logarithmic slope of the IMF, x, at the main sequence turnoff point. The logarithmic evolution of the luminosity per logarithmic time (dlnL / dlnt) scales linearly with x, at least for plausible values of x (see also van Dokkum 2008, Conroy, Gunn & White 2009). This dependency arises because the giant branch dominates the luminosity for all plausible values of x, and so the IMF determines the rate at which the giant branch is fed by turnoff stars. Steeper IMFs imply that the giant branch is more richly populated with time, and therefore the natural luminosity dimming is reduced. For sufficiently steep IMFs (e.g., x ≳ 5), the unevolving dwarfs would dominate the light, and so the integrated luminosity would be approximately constant over time.
It is somewhat less-well appreciated that the IMF above 1 M⊙ also strongly affects the shape of the SED of composite stellar populations. In composite populations the SED is influenced by stars with a range of masses (see Section 2.3), and so the IMF must play an important role (see e.g., Pforr, Maraston & Tonini 2012).
Interstellar dust is a component of nearly all galaxies, especially those that are actively star-forming. Dust plays a dual role in SPS, both as an obscurer of light in the UV through NIR and as an emitter of light in the IR. For both historical and theoretical reasons these two aspects are often modeled independently of one another. Indeed, these two aspects are sensitive to different properties of a galaxy (e.g., dust obscuration is highly sensitive to geometry while dust emission is more sensitive to the interstellar radiation field), and so it is not unreasonable to decouple the modeling of these two components.
2.2.1. Attenuation. Dust grains obscure light by both absorbing and scattering starlight. From observations of individual stars one can infer the total extinction along the line of sight by comparing an observed spectrum to the expected spectrum of the star in the absence of dust (the latter is typically obtained from models in conjunction with an estimated Teff and log g of the source). Thus, extinction measures the total loss of light along a single line of sight. Observations in the Milky Way (MW) and Large and Small Magellanic Clouds (LMC and SMC, respectively) have been obtained for a number of sightlines, enabling construction of average extinction curves for these galaxies (Cardelli, Clayton & Mathis 1989, Pei 1992, Gordon & Clayton 1998). In the MW and LMC the only striking feature in the extinction curve is the broad absorption at 2175 Å . This feature is absent in three out of four sightlines to the SMC, and it is weaker in the LMC than in the MW. The grain population responsible for this feature is not known, but polycyclic aromatic hydrocarbons (PAHs) are a leading candidate (Draine 2003). In general, dust extinction is a consequence of the optical properties of the grains and the grain size and shape distribution (Weingartner & Draine 2001).
When modeling SEDs of galaxies, the relevant concept is dust attenuation, which differs from extinction in two important respects: (1) light can be scattered both out of and into a given line of sight; (2) the geometrical distribution of dust with respect to the stars strongly affects the resulting SED (see Calzetti 2001 for an extensive discussion of these issues). The total dust attenuation in a galaxy can be estimated by analogy with how one estimates dust extinction: a spectrum of a galaxy is obtained and compared with the expected spectrum of the same galaxy in the absence of dust. For obvious reasons, estimating dust attenuation is considerably more complex than estimating dust extinction.
Although the shape of the dust attenuation curve depends on the star-dust geometry, grain size distribution, etc., in a complex manner, several general rules of thumb can be stated (see e.g., Witt & Gordon 2000 for a more thorough discussion). The simplest dust geometry, that of a homogenous foreground screen, yields an attenuation curve whose shape depends only weakly on the total dust column density (the weak dependence arises from the scattered light component). More complex geometries generally yield attenuation curves that become greyer (i.e., shallower) as the column density increases. Clumpy interstellar media also result in greyer attenuation curves than their homogenous counterparts. In all cases, the total attenuation optical depth is less than the amount of extinction that would be produced by the same column density because some scattered light is always returned to the line-of-sight. Finally, because the 2175 Å dust feature is believed to be due to pure absorption, the effects of radiative transfer will cause this feature to respond differently to geometrical effects compared to the rest of the attenuation curve. The use of a single dust attenuation curve for analyzing a wide range of SED types is therefore without theoretical justification.
In practice, most SPS modelers include dust attenuation by fixing the shape of the attenuation curve and fitting for the normalization. Popular attenuation curves include the Calzetti law, the MW, LMC, and SMC extinction curves, or the time-dependent attenuation model from Charlot & Fall (2000). The impact of the chosen attenuation curve on derived properties of galaxies will be discussed in later sections.
2.2.2. Emission. Beyond λ ~ 10 μm the SEDs of normal galaxies are dominated by emission from dust grains. Mathis, Rumpl & Nordsieck (1977) were the first to postulate that the dust grain population is comprised of both silicate and carbonaceous grains. In modern theories, the carbonaceous grains are assumed to be PAHs when they are small, and graphite when they are large (Draine 2003). The observed dust emission spectrum results from exposing these grains to a range of interstellar radiation field strengths.
A variety of models exist that combine grain size distributions and grain optical properties with models for starlight (or simply the radiation field) to predict IR emission (Desert, Boulanger & Puget 1990, Silva et al. 1998, Devriendt, Guiderdoni & Sadat 1999, Popescu et al. 2000, Dale et al. 2001, Piovan, Tantalo & Chiosi 2006, Jonsson 2006, Draine & Li 2007, Groves et al. 2008, Popescu et al. 2011). The modeling of PAH emission features (the most prominent being at 3.6 μm, 6.2 μm, 7.7 μm, 8.6 μm, and 11.3 μm) has become dramatically more sophisticated since the early attempts by Desert, Boulanger & Puget (1990), culminating in state-of-the-art models by Draine & Li (2007). At long wavelengths (λ > 50 μm) the emission is dominated by grains at a nearly steady temperature of ~ 15-20 K and contributes ~ 2/3 of the total IR luminosity. At shorter wavelengths the IR emission arises from single photon heating of dust grains (including PAHs) and accounts for the remaining ~ 1/3 of the total IR emission (see the review by Draine 2003 for details). The IR emission at the shortest wavelengths (λ < 12 μm) is supplied almost entirely by PAHs. In detail these relative contributions will depend on the grain composition and size distribution and the interstellar radiation field.
The models listed above are not always well-suited for interpreting large numbers of observed IR SEDs because they contain a large number of parameters, require knowledge of the star-dust geometry, and/or require radiative transfer calculations. Simpler models for dust emission have therefore been developed in parallel to the more complex ones. The IR templates of Chary & Elbaz (2001) and Dale et al. (2001) are widely used for estimating bolometric luminosities and k-corrections. These templates are based on sophisticated models, but are constrained to match observations of normal star-forming and starburst (i.e., ULIRG) galaxies. The resulting templates are functions of only one variable. For example, the Chary & Elbaz (2001) templates are a function of the bolometric IR luminosity. da Cunha, Charlot & Elbaz (2008) have developed a simple phenomenological model for dust emission that consists of a series of modified blackbodies for the thermal dust emission and for the emission from stochastically heated dust grains. In addition, they include an empirical spectrum of M17 to represent the PAH emission.
2.2.3. Dust Around AGB Stars. Stars experience very high mass-loss rates as they climb up the AGB (as high as 10-4 M⊙ yr-1 in the superwind phase). The mass lost is often observed to be dust rich (Bedijn 1987). These stars are often heavily dust obscured in the optical and emit copiously in the IR; they are often so dusty that their SEDs peak at ~ 10 μm (Bedijn 1987). Dust around AGB stars is important from the standpoint of SPS for two reasons: it will diminish the importance of AGB light in the optical and NIR, and it will contribute additional flux in the mid-IR beyond what would be expected from standard dust models (see e.g., Kelson & Holden 2010).
Despite the obvious importance of AGB dust, this aspect is included in few SPS models. Notable exceptions include the models of Bressan, Granato & Silva (1998) Silva et al. (1998), Piovan, Tantalo & Chiosi (2003), and González-Lópezlira et al. (2010), which are all based on theoretical models for AGB stars, their mass-loss rates, and dust formation and composition. Even the use of currently available empirical libraries of AGB stellar spectra require reddening the spectra to account for circumstellar dust (Lançon & Mouhcine 2002). Increasingly sophisticated radiative transfer models of dusty circumstellar envelopes are being developed (e.g., Groenewegen 2012, Sargent, Srinivasan & Meixner 2011, Srinivasan, Sargent & Meixner 2011). The outputs from these models should be incorporated into SPS codes as a standard practice.
2.3. Composite Stellar Populations
The simple stellar populations discussed in Section 2.1 are the building blocks for more complex stellar systems. Composite stellar populations (CSPs) differ from simple ones in three respects: (1) they contain stars with a range of ages given by their SFH; (2) they contain stars with a range in metallicities as given by their time-dependent metallicity distribution function, P(Z, t); (3) they contain dust. These components are combined in the following way:
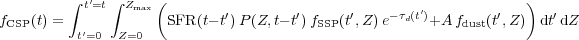 |
(2) |
where the integration variables are the stellar population age, t', and metallicity, Z. Time-dependent dust attenuation is modeled via the dust optical depth, τd(t') and dust emission is incorporated in the parameter fdust. The normalization constant A is set by balancing the luminosity absorbed by dust with the total luminosity re-radiated by dust.
The SFH can in principle be arbitrarily complex, although simple forms are usually adopted. By far the most popular is the exponential, or τ-model, where SFR ∝ e-t/τ. This form arises naturally in scenarios where the SFR depends linearly on the gas density in a closed-box model (Schmidt 1959). Recently, rising SFHs have become popular to explain the SEDs of high-redshift galaxies (Maraston et al. 2010, Papovich et al. 2011). Rising SFHs at early times seem to be a natural consequence of galaxy evolution in a hierarchical universe (Finlator, Davé & Oppenheimer 2007, Lee et al. 2010). Functional forms that incorporate an early phase of rising SFRs with late-time decay, such as SFR ∝ tβ e-t/τ, may therefore become more popular amongst modelers.
The treatment of metallicity in composite stellar populations is usually even more simplistic than the treatment of SFRs. The widely adopted simplification is to replace P(Z, t) in Equation 2 with a δ-function. In other words, a single metallicity is assumed for the entire composite population. The impact of this simplification on the SPS modeling procedure has not been extensively explored.
The approach to Equation 2 outlined above is standard but not universal. A notable exception is the technique of fitting non-parametric SFHs and metallicity histories in either a pre-defined or adaptive set of age bins (Cid Fernandes et al. 2005, Ocvirk et al. 2006, Tojeiro et al. 2009). The latter approach is computationally expensive since as many as thirty parameters are simultaneously fit to the data. Very high quality data are also a prerequisite for non-parametric techniques. Nonetheless, they offer the promise of less biased reconstruction of the SFH and metallicity history of galaxies based solely on their SEDs.
Figure 5 presents some basic properties of CSPs. The top panels show the fractional flux contribution from stars in different evolutionary phases for three representative SFHs. At late times the RGB and red HB dominate the red and NIR flux of τ-model SFHs, as is well-known. However, at young ages and/or for rising SFHs, the red and NIR are also influenced strongly by AGB stars, suggesting that the NIR can be susceptible to large uncertainties (due to uncertainties in the modeling of the AGB, as discussed in detail in later sections). The lower left panel shows the fractional flux contribution from stars more massive than 20 M⊙ and 60 M⊙ for a τ = 10 Gyr SFH. Massive star evolution is uncertain due to the complicating effects of rotation and binarity, and so this panel provides a rough sense of the extent to which uncertainties in massive star evolution will affect SED modeling. Finally, the lower right panel shows the light-weighted age as a function of wavelength, again for a τ = 10 Gyr SFH. The dashed line indicates the mass-weighted mean age. Already by 0.5 μm (approximately the V-band), the light-weighted age reaches its maximal value, again suggesting that going to redder restframe wavelengths is not providing substantial new information on the SFH. Notice also that the maximum light-weighted age never reaches the mass-weighted age. We return to this point in Section 4.
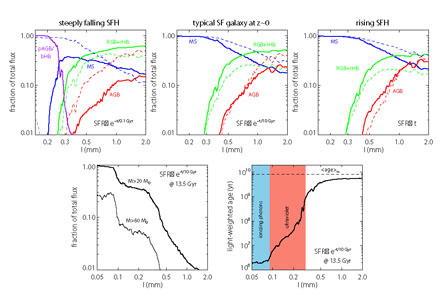 |
Figure 5. Top Panels: Fractional contribution to the total flux from stars in various evolutionary phases, for three different SFHs. The left panel is representative of a galaxy that formed nearly all of its stars very rapidly at early times, the middle panel is representative of a typical star-forming galaxy at z ~ 0, and the right panel may be representative of the typical galaxy at high redshift. Flux contributions are at 13 Gyr (solid lines) and 1 Gyr (dashed lines) after the commencement of star formation; all models are solar metallicity, dust-free, and are from FSPS (v2.3; Conroy, Gunn & White 2009). Labeled phases include the main sequence (MS), red giant branch (RGB), asymptotic giant branch (AGB, including the TP-AGB), post-AGB (pAGB), and the blue and red horizontal branch (bHB and rHB). Bottom Left Panel: Fractional flux contributions for stars more massive than 20 M⊙ and 60 M⊙ for the SFH in the middle panel of the top row. Bottom Right Panel: Light-weighted age as a function of wavelength for the same SFH. The dashed line indicates the corresponding mass-weighted age. |
Although the effects of nebular emission on SEDs will not be discussed in detail in this review, a brief overview of this component is given for completeness.
Nebular emission is comprised of two components: continuum emission consisting of free-free, free-bound, and two photon emission, and recombination line emission. Several photoionization codes exist that make predictions for the nebular emission as a function of the physical state of the gas, including CLOUDY (Ferland et al. 1998) and MAPPINGSIII (Groves, Dopita & Sutherland 2004). Other approaches can be taken to the modeling of nebular emission lines. For example, Anders & Fritze-von Alvensleben (2003) implement non-hydrogen emission lines based on observed line ratios as a function of metallicity. The nebular emission model must then be self-consistently coupled to a model for the starlight. Several groups have done this, with varying degrees of complexity, and with some only including nebular continuum, others only line emission, and others including both (e.g., Leitherer et al. 1999, Charlot & Longhetti 2001, Panuzzo et al. 2003, Groves et al. 2008, Mollá, García-Vargas & Bressan 2009, Schaerer & de Barros 2010).
The effect of nebular emission on the SED is complex, especially when line emission is considered. As a general rule, nebular emission is more important at low metallicity and at young ages. In such cases the contribution of nebular emission to broadband fluxes can be as high as 20-60% (Anders & Fritze-von Alvensleben 2003). Nebular emission will also be more important at high redshift because a feature with a fixed restframe EW will occupy a larger fraction of the filter bandpass due to the redshifting of the spectrum. The effect of nebular emission therefore cannot be ignored at high redshift, where high SFR, low metallicity galaxies are common (Schaerer & de Barros 2010, Atek et al. 2011).
It is noteworthy that amongst the most widely used SPS codes, including Bruzual & Charlot (2003), Maraston (2005), PEGASE (Fioc & Rocca-Volmerange 1997), STARBURST99 (Leitherer et al. 1999), and FSPS (Conroy, Gunn & White 2009), only PEGASE and STARBURST99 include nebular continuum emission, and only PEGASE includes both nebular continuum and line emission. Since nebular emission is relatively straightforward to implement (notwithstanding assumptions about the physical state of the gas), it should be a standard component of all SPS codes.
The SPS models described in this section are most frequently used to measure physical parameters of stellar populations. This is achieved by fitting the models to data, either in the form of broadband SEDs, moderate-resolution optical/NIR spectra, or spectral indices. The SSPs are usually taken as given, and the user then fits for a variety of parameters including metallicity, dust attenuation, and one or more parameters for the SFH. If IR data are available, then additional variables must be considered. The fitting techniques vary but are generally limited to grid-based χ2 minimization techniques. As the number of parameters increases Markov Chain Monte Carlo techniques become increasingly more efficient (Conroy, Gunn & White 2009, Acquaviva, Gawiser & Guaita 2011). One must also be aware of the influence of the chosen priors on the derived parameters; in cases where parameters are poorly constrained the prior can have a significant effect on the best-fit values (see e.g., Kauffmann et al. 2003, Salim et al. 2007, Taylor et al. 2011 for discussion). Moreover, it is highly advisable to derive the `best-fit' parameters from the marginalized posterior distribution, rather than from the minimum of χ2, since the likelihood surface can often be highly irregular (see e.g., Bundy, Ellis & Conselice 2005, Taylor et al. 2011).
When fitting SEDs it is important to remember that only the shape is being used to constrain the model parameters. In other words, the SED shape (or, more crudely, broadband colors) constrains parameters such as M / L, specific SFR (SSFR ≡ SFR / M), dust attenuation and metallicity. To obtain stellar masses one needs to multiply M / L by the observed luminosity and to obtain SFRs one then multiplies SSFR by M. This also holds true for M / L ratios and SSFRs inferred from EWs of emission lines, spectral indices, and full spectral fitting.
The reader is referred to Walcher et al. (2011) for further details on SED fitting techniques.