Figure 53 makes this point concrete.
 |
Figure 52. What is an elliptical galaxy?
Morphologically, the dwarf galaxy Leo I (top-middle panel)
resembles the dwarf irregulars Leo A and GR 8 in its low surface
brightness and shallow brightness gradient. But it resembles the giant
elliptical M 87 in having elliptical isophotes
and no cold gas. Since only the latter characteristics morphologically
define ellipticals, Leo I is often called a "dwarf elliptical". However,
purely morphological criteria prove unable to distinguish objects that have
different formation histories. Leo I turns out to be related to dI
galaxies, not to ellipticals. So I do not call it a dwarf elliptical;
rather, I call it a dwarf spheroidal (dSph) galaxy. |
Who does not belong in Fig. 53? The answer is
of course well known (Fig. 54). Dolphins
(Fig. 53, top right) are
mammals, even though they are morphologically similar to sharks
(Fig. 53, top left). To make a living, both
need to be well streamlined,
strong swimmers. Convergent evolution made them that way. In contrast, a
leafy seadragon (Fig. 53, bottom right:
http://picasaweb.google.com/lh/photo/cEq5cwlB2_cmufKXlOKJcg) is
a kind of seahorse whose main need is good camouflage to avoid
predators. So, even though it is a fish, its morphology has evolved to
be very different from that of a shark. A "Hubble classification" of
sea animals that was superficially based on visible structural
characteristics could mistakenly combine sharks and dolphins into the
same or closely related classification bins and could miss the more
subtle (but more important) differences that distinguish sharks and sea
dragons from dolphins and cows. Which parameters best distinguish the
physical differences that are most important to us is not necessarily
obvious without detailed study.
 |
Figure 53. The danger of classifying using
only morphology. Who does not belong? |
 |
Figure 54. Dolphins are Mammals. Convergent
evolution happens. It happens to galaxies as well as to creatures on
Earth, and elliptical and spheroidal galaxies prove to be
examples. They look morphologically similar but have different
formation histories. I warmly thank Douglas Martin
(http://www.dolphinandcow.com) for permission to use
this figure. |
7.2. The E – Sph dichotomy
Why did we ever think that Leo I and NGC 205 are ellipticals? The answer
is that research on galaxies began with descriptive classical morphology
(e. g.,
Hubble 1936;
de Vaucouleurs 1959;
Sandage 1961),
and then the
above galaxies satisfy the definition of an elliptical. However, we
will see in Fig. 59 that
Sandage et al. (1985b)
had no trouble in
distinguishing between E and dE galaxies of the same luminosity. If
this sounds surpassingly strange to you, you have the right reaction. I
will come back to this point below.
Astronomers are conservative people – this is often healthy
– and most people clung to the idea that galaxies like Leo I and
NGC 205 are ellipticals even after hints to the
contrary started to appear. Figure 55 shows an
example. Ellipticals (filled circles) have
higher surface brightness at lower galaxy luminosities, whereas "dwarf
ellipticals" (open circles and crosses) have lower surface brightnesses
at lower luminosities. M 32 is consistent with the extrapolation of the
E sequence. However, at that time, we thought that M 32 is compact
because it has been tidally truncated by M 31
(King 1962;
Faber 1973).
Bingelli et al.
(1984)
therefore concluded that E and dE
galaxies form a continuous but not monotonic sequence in surface
brightness as a function of luminosity. Meanwhile, one could wonder
whether the two sequences in Fig. 55 already
hint at different formation physics.
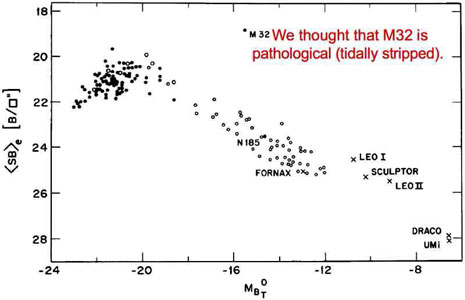 |
Figure 55. Parameter correlations for
elliptical and "dwarf elliptical" galaxies from
Bingelli et al.
(1984).
These authors suggested that giant and dwarf ellipticals
form a continuous but not monotonic sequence in mean surface brightness
as a function of absolute magnitude MBT and that M 32 – which deviates prominently from this
sequence – is pathological. |
Wirth & Gallagher
(1984)
were the first to suggest that M 32-like
compact ellipticals and not the more diffuse galaxies like Draco and
Leo I and NGC 205 form the faint end of the luminosity sequence of
elliptical galaxies. This was based on a successful search for
relatively isolated dwarf compact ellipticals which resemble
M 32. The new compact ellipticals and the well known
ones that are
companions to larger galaxies were found to lie along the extrapolation
to lower luminosity of the correlations for normal ellipticals of
parameters such as effective radius and velocity dispersion. With
respect to this family of normal ellipticals, "the diffuse ellipticals
are a distinct structural family of spheroids whose properties begin to
diverge from those of the classical ellipticals at an absolute magnitude
of MB ~ -18. At MV = -15,
these two families differ in mean surface brightness by nearly two
orders of magnitude. The key point to note for this discussion is that,
in the range -18  MB
MB
 -15, both
structural classes of elliptical galaxies coexist"
(Wirth & Gallagher
1984).
This implies that the luminosity functions of elliptical and spheroidal
galaxies differ as shown in Fig. 56.
-15, both
structural classes of elliptical galaxies coexist"
(Wirth & Gallagher
1984).
This implies that the luminosity functions of elliptical and spheroidal
galaxies differ as shown in Fig. 56.
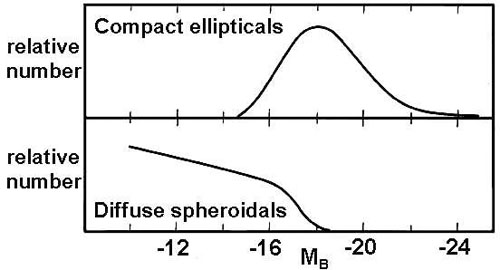 |
Figure 56. Luminosity functions of (top)
normal elliptical galaxies roughly from M 32 to M 87 and
(bottom) spheroidal galaxies roughly from Draco and UMi to galaxies such as NGC 205
(Wirth & Gallagher
1984).
At that time, "spheroidals" were commonly called "dwarf ellipticals".
This figure then shows that the smallest non-dwarf ellipticals have
lower luminosity than the biggest dwarf ellipticals. |
The
Wirth & Gallagher
(1984)
paper was largely based on four newly
found, free-flying compact ellipticals. The competing idea
(Faber 1973)
that compact ellipticals are tidally truncated was largely based on
three galaxies, M 32, NGC 4486B and NGC 5846A; then the diffuse dwarfs
would be the faint extension of the E sequence. With both conclusions
based on small numbers of galaxies, it was not clear which picture is
correct. The rest of this section reviews the now very strong evidence
that
Wirth & Gallagher
(1984)
were presciently close to correct in
almost every detail, including Fig. 56.
As a graduate student at Caltech in the early 1970s, I was brought up on
the picture that ellipticals form a continuous, non-monotonic sequence
in their structural parameters from the brightest to the faintest
galaxies known. Then, in the 1980s, I gained access to two important
technical advances. The first was CCD detectors that are linear in
sensitivity over large dynamic ranges. The second was the
Canada-France-Hawaii telescope (CFHT), which had the best "seeing" then
available on any optical telescope. These allowed me to study the
central structure of galaxies in unprecedented detail. The results
revolutionized my picture of ellipticals. They confirmed and extended
Wirth & Gallagher
(1984),
whose ideas I was not aware of until the end of my work. The story is
instructive for students, so I describe it here in detail, abstracted
from a popular article in Stardate magazine
(Kormendy 2008b).
My CFHT surface photometry showed an unexpected result
(Fig. 57). Ellipticals define the sequence of
red points: less luminous
ones are smaller and higher in surface brightness from M 87 to
M 32. This much was expected; for bright galaxies,
it is the correlation shown by the filled circles in
Fig. 55. Importantly, the
high-resolution CFHT photometry helps to fill in the gap between M 32
and the other ellipticals. This makes M 32 look less peculiar.
The surprise was the behavior of the "dwarf ellipticals", shown in
Fig. 57 by yellow points. Using near-central
parameters rather than parameters measured within the effective radii
re as in Fig. 55, it is clear
that dwarf ellipticals
do not satisfy the correlations for elliptical galaxies. Less luminous
dwarf ellipticals are lower – not higher – in surface
brightness. A gap has appeared between ordinary and dwarf ellipticals.
Wirth & Gallagher's
(1984)
conclusions are confirmed with a much larger sample.
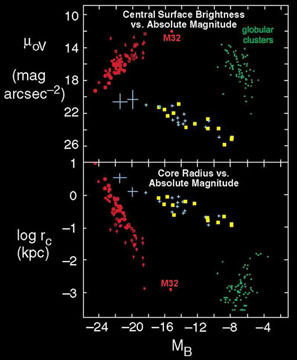 |
Figure 57.
Kormendy (1985,
1987)
showed with much larger samples that E and Sph
galaxies form disjoint sequences in parameter space (cf.
Wirth & Gallagher
1984).
Sphs (yellow) are not faint ellipticals (red). Instead, their parameter
correlations are almost identical to those of dwarf spiral and irregular
galaxies (blue). This figure shows approximate central surface brightness
and
King (1966)
core radius, both corrected as well as possible for PSF blurring,
versus B-band absolute magnitude. |
Size and density are diagnostic of galaxy formation, so I realized at
this point that dwarf ellipticals are not ellipticals at all.
As one point after another got plotted and intermediate cases failed to
show up, my previous picture of elliptical galaxies fell apart.
Kuhn (1970)
captures exactly what happens in a scientist's mind when his
understanding of a subject falls apart. Quoting
Kormendy (2008b):
"The first reaction was consternation. What have I screwed up? I checked
my data reduction. I considered whether my galaxy sample
could be biased. Nothing seemed wrong. Better data just led in an
unexpected direction. I had to accept the new result: dwarf ellipticals
are not ellipticals. But then we should not call them "dwarf
ellipticals". The smallest such companions to our Milky Way had
sometimes been called dwarf spheroidals. So, to minimize the departure
from tradition, I called all such objects "spheroidals".
The biggest ones in Virgo are only as luminous as an average elliptical,
but they are giant spheroidals."
"If spheroidals are not ellipticals, what are they? Kuhn describes what
happens next. Deprived of the guidance of any previous understanding of
a subject, a scientist in the midst of a scientific revolution does not
know what to do next. In turmoil and in desperation, wild ideas get
tried out, most of them wrong. I plotted in my diagrams all the other
kinds of stellar systems that I knew about. I plotted globular clusters
of stars [green points], spiral galaxy disks [two large blue plus signs,
each an average for several galaxies from
Freeman 1970],
and irregular
galaxies [blue plus signs]. The globulars were unconnected with
ellipticals and spheroidals. But the irregulars and spirals were a
surprise. They showed exactly the same correlations as the
spheroidals. Aha! A new picture was emerging. Maybe spheroidals are
related to spirals and irregulars. They have almost the same
structure. They don't contain gas and young stars, which are common in
spirals and irregulars. And they have smoother structure. But I realized
that, if the gas were removed or converted into stars, dynamical
evolution of the now-gasless spheroidal would smooth out its formerly
patchy structure within a few galactic rotations. We knew that the dwarf
spheroidal companions of the Milky Way had varied star formation
histories. A few contain only old stars, as ellipticals do, but most
experienced several bursts of star formation, and the most recent burst
was a few billion or even as little as a few hundred million years
ago. What are galaxies that have not yet had their last burst of star
formation and that therefore still must contain gas? This is not a
controversial question
[Kormendy & Bender
1994].
They are irregulars. I realized: if we looked at the Milky Way's dwarf
spheroidals when the Universe was half of its present age, about half of
them would still be irregulars. Irregulars have been turning into Sphs
gradually over most of the history of the Universe. In the
Virgo cluster, lots of processes can make this
happen. The most obvious is
ram-pressure stripping: as an irregular galaxy falls into Virgo for the
first time, it rams into the million-degree gas that fills the cluster,
and its cold gas gets swept away. It started to look like no accident
that the irregulars in Virgo live around the outside of the cluster,
while the center is inhabited by spheroidals
[Binggeli et al.
1987]."
"Within a few days, I had a new picture. Spheroidals are defunct spiral
and irregular galaxies converted by their environment to look like
ellipticals. This helped our picture of galaxy formation, because we
already knew that ellipticals form by galaxy mergers, whereas, quoting
Tremaine (1981),
`Dwarf elliptical satellite galaxies cannot form by
mergers with other satellites since their relative velocities are too
high.' We were in trouble when we had to find a single formation process
that could explain NGC 4472, one of the biggest galaxies in the nearby
Universe, and dwarf spheroidals that are a million times less luminous
and that look like fragile, gossamer clouds of stars
[Fig. 58
here]. But they look like the smallest irregulars, minus gas and young
stars [Fig. 52 here]. So this problem was
solved. I reported these
results [at a workshop in Rehovot, Israel], and they were well
received." The result that E and Sph galaxies are different is called
the E – Sph dichotomy.
 |
Figure 58. Luminosity sequence of dSph
satellites of our Galaxy. Fornax, Sculptor and Draco have absolute
magnitudes of MV = -13.2, -11.1 and -8.8,
respectively
(Mateo 1998),
and correspondingly decreasing surface
brightnesses (see Fig. 57). Draco is the cloud
of faint stars in the
right panel; the bright stars with the instrumentally-produced red
halos are foreground stars in our Galaxy. Contrast M 87 in
Fig. 52. Could M 87 and Draco really have
similar formation
histories, with different results only because changing the mass tweaks
the formation physics? The results reviewed here imply that the answer
is "no". We now believe that M 87 is a remnant of the dynamical
violence of galaxy mergers, whereas Draco formed quescently as a dwarf
irregular that lost its gas long ago. From
Kormendy (2008b). |
7.3. Mixed reactions to the E – Sph
dichotomy
Scientific research is a quintessentially human enterprise, as reactions
to the above result illustrate:
The essential theoretical understanding of why Sph and S+Im galaxies
have lower stellar densities at lower galaxy masses followed
immediately.
Dekel & Silk (1986)
"suggest that both the dI's and
the dE's [here: dSphs] have lost most of their mass in
[supernova-driven] winds after the first burst of star formation, and
that this process determined their final structural relations. The dI's
somehow managed to retain a small fraction of their original gas, while
the dE's either have lost all of their gas at the first burst of star
formation or passed through a dI stage before they lost the rest of the
gas and turned dE." Our story here adds detail on dI → dSph
transformation processes but otherwise is based on exactly the above
picture.
Reactions among observers have been more mixed. The reasons are many and
revealing and occasionally entertaining; they range from innate
conservatism to specific scientific arguments to turf wars. I will
concentrate on the part of this history that is most instructive for
students.
I already noted that many astronomers are conservative: they do not
easily discard a picture that they believed in for many years. This is
healthy – imagine what would happen if we chased, willy-nilly,
after every outrageous idea that got proposed. It is prudent to treat
new ideas with respect, but in a mature subject, it is uncommon for a
long-held, well-supported picture to be completely wrong. The situation
is more tricky when subjects are young and not yet well developed. This
proved to be such a case. Nevertheless, it is understandable that people
who had long been involved in research on dwarf galaxies reacted to the
above developments with some ambivalence. In particular, the group of
Sandage, Binggeli, Tammann and Tarenghi wrote a series of papers on the
Virgo cluster in the mid-1980s, some before and some
after the
Wirth & Gallagher
(1984)
and
Kormendy (1985,
1987)
papers. Struggles with
the new ideas were evident in some of the later papers. The nature of
these struggles reveals how seeds of the new ideas could have been
recognized in the older results. I belabor this point because the
conceptual blindness that results when we embrace a paradigm of how
nature works always threatens our ability to see something new. As
you do your research, it is healthy to be careful and conservative but
also prudent to ask yourself: Am I missing something because of
paradigm-induced conceptual blindness?
Kuhn (1970)
provides a perceptive discussion of this subject.
Figure 55 already illustrated how one hint
– the opposite slopes
of the surface-brightness–luminosity correlations – was
contained in previous work.
Figure 59 is a better illustration
(Sandage et al.
1985b).
It shows with data on Virgo galaxies the result that is shown
schematically in Fig. 56. The luminosity
function of ellipticals is bounded at high and low L. M 32
has normal properties for its low luminosity, but such tiny ellipticals
are rare. In contrast, spheroidal galaxies (which
Sandage et al.
1985b
call "dEs")
never are very bright, but they get rapidly more common at lower
luminosities until they are lost in the detection noise.
The steep faint-end slope of the luminosity function had been recognized
for a long time
(Zwicky 1942,
1951,
1957)
and is built into the well known
Schechter (1976)
analytic luminosity function.
But, to the best of my knowledge, Sandage et al.
(1985a,
b)
and
Binggeli et al.
(1988)
were the first to measure luminosity functions separately
for different morphological types of galaxies and to show that only Sph
galaxies have luminosity functions that continue to rise with
decreasing luminosity to the detection limit of the data. This is the
solid result in Fig. 59. Here is the incongruity:
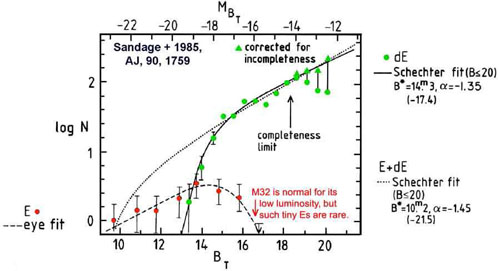 |
Figure 59. Luminosity functions of
elliptical and spheroidal galaxies in the Virgo cluster. This figure is adapted from
Sandage et al.
(1985b),
who used the traditional name "dE" for
spheroidals. I have updated the Hubble constant from
H0 = 50 to 70 km s-1 Mpc-1.
Magnitudes are in B band. From
Kormendy & Bender
(2012). |
Sandage et
al. (1985b)
distinguish between elliptical and dwarf elliptical galaxies of the same
luminosity. Quoting
Kormendy & Bender
(2012):
"A dwarf version of a creature is one that, when mature, is smaller than
the normal sizes of non-dwarf versions of that creature. ... And yet,
[Fig. 59] invites us to imagine that the
smallest non-dwarf ellipticals are
20 times less luminous than the brightest `dwarf ellipticals'."
Sandage and collaborators recognized and struggled with this
incongruity. Quoting
Sandage & Binggeli
(1984):
"The distinction
between E and dE types is made on morphological grounds alone, using
surface brightness as the criterion. Normal E galaxies have a steep
radial profle (generally following an r1/4 law) with
high central brightness. The typical dE has a nearly flat radial
profile, following either a
King (1966)
model with a small concentration
index or equally well an exponential law. The morphological transition
from E to dE is roughly at MB ≃ -18, but there
is overlap." Recognition of this difference dates back at least to
Baade (1944):
"NGC 147 and NGC 185 are elliptical nebulae of very low
luminosity. In structure, they deviate considerably from what is
considered the typical E-type nebula. In both objects the density
gradient is abnormally low."
Binggeli et al.
(1985)
also recognized the quantitative similarity beween spheroidals and
irregulars; their Virgo "membership criteria applied are: (1) dE and Im
members have low surface brightness. ...". Soon afterward,
Sandage et al.
(1985b)
admit that "We are not certain if this [E –
dE dichotomy] is totally a tautology due merely to the arbitrary
classification criteria that separate E from dE types ... or if the
faint cutoff in the [E luminosity function] has physical meaning related
to the properties of E and dE types. In the first case, the problem
would be only one of definition. In the second, the fundamental
difference in the forms of the luminosity functions of E and dE types
... would suggest that two separate physical families may, in fact,
exist with no continuity between them (cf.
Kormendy 1985
for a
similar conclusion)." Revising a long-held picture can be uncomfortable.
Within a few more years,
Binggeli et al.
(1988)
recognized that
"The distinction [between] Es and dEs must almost certainly mean that
the two classes are of different origin
(Kormendy 1985,
Dekel & Silk 1986).
This is also supported by the fact that the luminosity functions
of Virgo Es and dEs [are different]." And
Binggeli & Cameron
(1991)
concluded that "there are no true intermediate types between E and
dE. The [E – dE] dichotomy is model-independent" (emphasis
in the original).
But psychology did not lose its hold on people. Binggeli changed his
mind: in a section entitled "The E–dE dichotomy and how it
disappears",
Jerjen & Binggeli
(1997)
emphasize the observation
that, in a plot of brightness profile Sérsic index versus
MBT, E and dE galaxies show a continuous
correlation. They conclude that compact ellipticals like M 32 and its analogs in Virgo are "special" and that dEs form the extension
of the ellipticals to low L. However, this is not the only relevant
correlation. The observations which suggest the dichotomy had not
disappeared. And the fact that one can find parameters of galaxies that
are insensitive to the differences between two types does not prove that
the two types are the same. Many parameters are continuous between
ellipticals and spheroidals. E. g., the content of heavy elements is not
only a continuous function of luminosity for ellipticals and
spheroidals, it is essentially the same continuous function for spirals
and irregulars, too (e. g.,
Mateo 1998).
If we looked only at element abundances, we would be blind to all
structural differences encoded in Hubble types.
More recent criticisms of the E – Sph dichotomy are reviewed in
Kormendy et al.
(2009)
and in
Kormendy & Bender
(2012).
The arguments involve technical details such as sample size and profile
analysis techniques. These are of less immediate interest, and any
discussion of them quickly gets long. I therefore refer readers to the
above papers for our answers to the criticisms. A few are relevant here
and will be discussed below. But the best way to address uncertainty
about the E – Sph dichotomy is to observe larger samples of
galaxies and to address more general scientific questions, as follows.
7.4. Confirming the E–Sph dichotomy with large
galaxy samples
Kormendy et al.
(2009:
KFCB)
extend the sample size of the parameter correlations in
Fig. 57 by measuring
brightness profiles for all known ellipticals in the Virgo cluster and
combining these with data on ~ 275 Sph galaxies.
Examples are shown in Fig. 60. Data from many
sources were combined to construct composite profiles over large dynamic
ranges. Sérsic functions fit most of the galaxy light to remarkable
precision: over the fit ranges (vertical dashes in
Fig. 60), the average RMS deviation = 0.040 mag
arcsec-2 for the whole
KFCB sample.
Kormendy (2009)
further added ellipticals from
Bender et al.
(1992)
and Sphs from
Chiboucas et al.
(2009).
The updated Fig. 57 is shown in
Fig. 61.
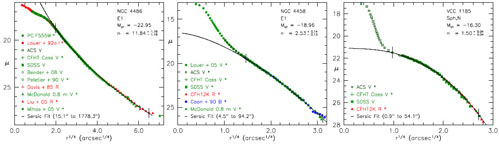 |
Figure 60. Surface brightness profiles of 3
galaxies from KFCB. NGC 4486 (M 87) is an elliptical galaxy with a
central "core"; i. e., central "missing light" with respect to the
inward extrapolation of the outer Sérsic function fit (black
curve). NGC 4458 is an elliptical galaxy with central
"extra light"
above the inward extrapolation of the outer Sérsic fit. VCC 1185
is a Sph galaxy with a nuclear star cluster (type Sph,N) in addition to
its Sérsic-function main body. This figure illustrates the robust
profiles that are derived by using many images that provide data in
overlapping ranges of radii (e. g.,HST data near the center;
large-field CFHT data at large r). |
Figure 61 strongly confirms the dichotomy
between E and Sph galaxies as found in
Kormendy (1985,
1987),
Binggeli & Cameron
(1991)
and Bender et al.
(1992,
1993).
Note that the Sph sequence approaches the E
sequence near its middle, not near its faint end.
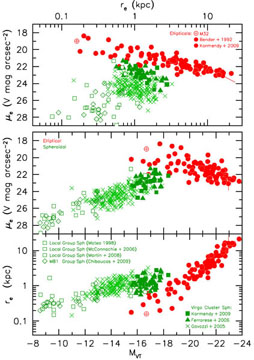 |
Figure 61. Global parameter correlations
from KFCB and
Kormendy (2009)
with Sph galaxies in the Local and M 81 groups updated from
Kormendy & Bender
(2012).
This figure shows 90
ellipticals and 295 spheroidals. One elliptical plots in the Sph
sequence when effective parameters are used; difficult cases such as
this one were classified in
KFCB using
parameters measured at the
radius that contains 10% of the total light. Reason: the E – Sph
dichotomy is most pronounced when near-central parameters are used
(contrast Fig. 57 with this figure). |
The small-re, bright-μe end of the
sequence of ellipticals is defined in part by galaxies like M 32 that
are sometimes called "compact ellipticals". As noted above, compact
ellipticals are not a special class. They are continuously connected
to brighter ellipticals in essentially all parameters. Moreover, M 32 is
no longer unique, as it appeared to be in
Fig. 57. We now know of a
number of M 32 analogs
(Binggeli et al.
1985;
Lauer et al.
1995;
Faber et al.
1997;
KFCB).
Figure 61 illustrates and
KFCB
reviews evidence that M 32 is normal for its low L. However, it
is often suggested that these galaxies are compact only because they
have been tidally stripped by much larger companions (e. g.,
Faber 1973;
Ferrarese et al.
2006;
Bekki et al.
2001;
Chen et al.
2010).
Kormendy & Bender
(2012)
review why it is not
plausible that this is the explanation for why small Es are compact.
This issue is important, so I enumerate the arguments here:
Compact
ellipticals are not always companions of brighter galaxies
(Wirth & Gallagher
1984).
Some are so isolated that no tidal encounter with a
big galaxy is likely ever to have happened (e. g., VCC 1871:
Kormendy & Bender
2012).
Compact Es do not have
small Sérsic indices suggestive of tidal truncation. In fact, they
have the same range of Sérsic indices n ~ 2 to 3.5 as
isolated coreless ellipticals. For example, M 32 has n ≃
2.9, larger than the median value for coreless ellipticals. Numerical
simulations show that major mergers of gas-poor galaxies like the ones
in the nearby Universe make remnants that have exactly the above range
of Sérsic indices
(Hopkins et al.
2009a).
Many Sph galaxies also are
companions of bright
galaxies, but we do not argue that they have been truncated amd thereby
made abnormally compact. An example is NGC 205, which is shown by the
open square at MVT = -16.6 in
Fig. 61. It is
much fluffier than M 32.
Figure 68 below
will show that the compact end of the E sequence is also defined by tiny
bulges. Classical bulges and ellipticals have closely similar parameter
correlations. Most classical bulges that appear in our correlation
diagrams do not have bright companion galaxies.
In
Fig. 61, the ellipticals from M 32 to cD
galaxies define projections of the "fundamental plane" correlations
(Djorgovski & Davis
1987;
Faber et al.
1987;
Djorgovski et
al. 1988;
Bender et al.
1992).
Its interpretation is well
known: galaxy parameters are controlled by the Virial theorem modified
by small nonhomologies. N-body simulations of major galaxy mergers
reproduce the E-galaxy fundamental plane, not the Sph parameter sequence
that is almost perpendicular to it
(Robertson et
al. 2006;
Hopkins et al.
2008,
2009b).
Kormendy and Bender conclude: "some compact Es may have been pruned
slightly, but tidal truncation is not the reason why the E sequence
extends to the left of where it is approached by the Sph sequence in
[Fig. 61]."
7.4.1. Classical bulges and ellipticals satisfy the
same fundamental plane parameter correlations. I. Bulge-disk
decomposition
Point (d) above anticipates the result of this subsection: classical
bulges are essentially indistinguishable from elliptical galaxies of the
same luminosity. This in turn was further anticipated when I defined
classical bulges to be elliptical galaxies that happen to live in the
middle of a disk. Here, the time has come to ante up the evidence by
adding classical bulges to Fig. 61.
Figure 62 emphasizes the most important
requirement for this
analysis. For each disk galaxy, it is necessary to decompose the
observed brightness distribution into (pseudo)bulge and disk parts. This
is a fundamental part of the classification of the central component as
classical or pseudo. It provides separately the parameters of the
bulge and the disk, both of which we need. For some applications, a
kinematic decomposition is also needed.
 |
Figure 62. (left) Sombrero Galaxy and
(right) NGC 4762, the second-brightest S0 galaxy in the
Virgo cluster. These galaxies illustrate why
bulge-disk decomposition is
necessary. NGC 4594 is an Sa galaxy with B / T = 0.93
± 0.02
(Kormendy 2011b).
Without photometric decomposition, we
measure essentially only the bulge. We learn nothing about the disk. If
an S0 version of this galaxy (e. g., NGC 3115) were viewed face-on, it
would be difficult even to discover the disk
(Hamabe 1982).
In contrast, NGC 4762 is an edge-on S0 with a tiny bulge; B /
T = 0.13 ± 0.02 (Fig. 63).
Without photometric
decomposition, we measure essentially only the disk. We learn nothing
about the bulge. |
Photometric decomposition is the crucial requirement that allows us to
ask whether classical bulges satisfy the parameter correlations for
ellipticals. Absent such a decomposition, even the distinction between
ellipticals and spheroidals is blurred. This is part of the reason why
Ferrarese et al.
(2006);
Chen et al.
(2010),
and
Glass et al.
(2011)
do not see the E – Sph dichotomy. If bulges
and disks are combined in various proportions and then measured as
one-component galaxies, it is inevitable that the resulting parameters
will be intermediate between those of bulges and disks and that
including them will blur the distinction between the bulge and Sph
≈ disk sequences in Fig. 61 (see Figs. 76
and 77 in KFCB and
Figs. 63 and 64 here).
The need for bulge-disk decomposition can best be understood using an
analogy. Imagine studying a population of people, horses and people who
ride on horses. Knowing nothing about them, one might measure parameters
and plot parameter correlations (linear size, mass, ...) to look for
different physical populations and regularities within each population
that might drive interpretation. We need to be careful, because some
parameters (volume mass density within this analogy; mass-to-light ratio
for galaxies) prove to be insensitive to structural differences. Still,
careful parameter study is promising. But the biggest people are bigger
than the smallest horses. If random people are paired with random horses
and the resulting population of people+horses, together with some pure
people and some pure horses, are analyzed as one-component systems, it
is inevitable that a complete continuity will be found between people
and horses. But it would be wrong to conclude that people are the same
as horses. Rather, if one decomposes people and horses when they occur
together and measures their parameters separately, it will be found that
some parameter correlations clearly separate people of various sizes
from horses of various sizes, even though their size distributions
overlap. Further study will also show that certain special parameters
(semi-trivially: number of arms versus number of legs in this analogy;
near-central parameters in the cases of galaxies) are especially helpful
in distinguishing the physically different populations that are under
study. The one elliptical galaxy (red point) that lies within the
sequence of Sphs (green points) in some panels of
Fig. 61 was
classified using central parameters (Fig. 34 in
KFCB).
It feels strange to "beat this dead horse" (I'm sorry – I could
not resist): the need for component decomposition has been understood
for more than 30 years. It quickly became standard analysis
(Kormendy 1977a;
Burstein 1979;
Kent 1985).
It is still so now
(Peng et al. 2002;
Knapen et al.
2003;
de Souza et al.
2004;
Laurikainen et
al. 2004,
2005,
2007;
Courteau et al.
2007;
Méndez-Abreu et
al. 2008;
Weinzirl et al.
2009).
The structure (this section) and formation physics
(Section 8) of bulges
and disks are very different, and it blurs our vision of both to analyze
them as single-component systems.
7.4.2. Small-bulge S0 galaxies and the transition
from S0 to Sph galaxies
Kormendy & Bender
(2012:
KB2012) collect bulge and disk parameters
from a variety of sources for or do photometry and bulge-disk
decomposition of all S0 galaxies from the HST ACS Virgo Cluster
survey
(Côté et
al. 2004;
Ferrarese et al.
2006).
This section reviews the results. Classical bulges are added to
the parameter correlation diagrams in Fig. 68.
But another and –
it will turn out – especially interesting result will be to extend
the Sph sequence to higher luminosities.
Kormendy & Bender
(2012)
conclude that Sph galaxies and S0 disks (but not bulges) are
continuous in their parameter correlations. That is, Sph galaxies are
bulgeless S0s.
Three galaxies serve here to illustrate the transition from S0 galaxies
with large classical bulges and flat disks to Sph galaxies with no
bulges and with structure that can be vertically disky or thick. We
start with NGC 4762. Figure 62 shows
that it
differs from our canonical picture of Hubble classification
(Sandage 1961)
in which S0
galaxies are transition objects between elliptical and Sa galaxies. The
bulge-to-total luminosity ratio B / T is a classification
parameter; B / T ≡ 1 for ellipticals, and B /
T is intended to decrease along the sequence E – S0 –
Sa – Sb – Sc. With some noise, this is observed
(Simien & de
Vaucouleurs 1986).
But
Sidney van den Bergh
(1976)
already recognized that some S0 galaxies such as NGC 4762 have small
bulges and, except for their cold gas content and spiral structure, are
more similar in their overall structure to Sbc galaxies than they are to Sa
galaxies. As an alternative to the
Hubble (1936)
"tuning-fork diagram",
he proposed a "parallel sequence classification" in which S0 galaxies
form a sequence S0a – S0b – S0c with decreasing B /
T that parallels the sequence Sa – Sb – Sc of spiral
galaxies with similar, decreasing B / T ratios. Van den
Bergh suggested that late-type S0 galaxies with small bulges are defunct
late-type spiral galaxies that were transformed by environmental
processes such as ram-pressure stripping of cold gas by hot gas in
clusters. The
KB2012
bulge-disk decompositions of NGC 4762 and similar
galaxies quantitatively confirm van den Bergh's picture, as follows.
The brightness profile of NGC 4762 measured along the major axis of the
disk is shown in Fig. 63 (left). It shows a
central bright and
relatively round bulge and, at larger radii, three shelves in a very
flat edge-on disk. The inner shelf is somewhat subtle, but the steep
decrease in surface brightness between the middle and outer shelves is
obvious in Fig. 62. What is this complicated
structure? This may seem
like a tricky problem, but in fact, it is easy. Relatively face-on
galaxies that have two or three shelves in their brightness
distributions are very common. The ones with two shelves are the
oval-disk galaxies discussed in
Section 3.3. To get a third shelf, it
is just necessary to add an early-type bar – these have shallow
radial brightness gradients interior to a sharp outer end. Now, the bar
normally fills its attendant lens in one dimension
(Section 4.3.4 and
Fig. 17). But consider a
non-edge-on SB(lens)0 galaxy such as NGC 2859
(Fig. 9) or NGC 2950
(Fig. 17) in which the bar has a skew
orientation (not along either the apparent major or apparent minor
axis). If we rotated either of these galaxies about a horizontal line
through the center in the corresponding figure until the galaxy was seen
edge-on, its disk would show three shelves in its major-axis
profile. Exterior to the bulge, the innermost shelf would be the bar,
the next would be the lens, and the third would be the outer disk. This
is how Kormendy & Bender interpret Fig. 63
(left). Thus NGC 4762
is an edge-on SB(lens)0 galaxy. Bars and lenses have shallow brightness
gradients at small r, so profile decomposition is easy. The
bulge Sérsic index n = 2.29 ± 0.05 and round shape
identify it as classical. Importantly, B / T = 0.13
± 0.02 is very small. So
Kormendy & Bender
(2012)
classify NGC 4762 as SB(lens)0bc. Note in
Fig. 63 (right) how measuring NGC 4762 as
a single-component system (green point with brown center) mixes
parameters of the classical bulge (brown point) and disk (green
cross). Only after bulge-disk decomposition do we see that the tiny
classical bulge of NGC 4762 helps to define the compact extension of the
E – bulge parameter sequence.
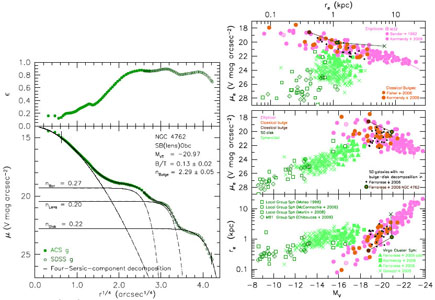 |
Figure 63.(left) Ellipticity and surface
brightness along the major axis of NGC 4762 measured by fitting
elliptses to the isophotes in the ACS and SDSS g-band
images. The dashed curves show a decomposition of the profile inside
the fit range (vertical dashes). The bulge, bar, lens and disk are
represented by Sérsic functions with indices n given in the
figure. Their sum (solid curve) fits the data with an RMS of 0.033 V
mag arcsec-2. (right) Parameter correlations showing the
results of the bulge-disk decomposition. The green filled circles with
the brown centers show the total parameters measured by
Ferrarese et
al. (2006)
for the bulge and disk together. They are connected by
straight lines to the parameters of the bulge (dark brown filled
circles) and disk (dark green crosses). From
KB2012. |
NGC 4452 is closely similar to NGC 4762 but is even more extreme.
Figure 64 (left) shows that it, too, is an
edge-on SB(lens)0 galaxy. The
decomposition robustly shows that NGC 4452 has only a very tiny
pseudobulge with n ≃ 1.06 ± 0.14 (recall
classification criterion (6) in
Section 5.3) and PB/T =
0.017 ± 0.004. This is an SB(lens)0c galaxy.
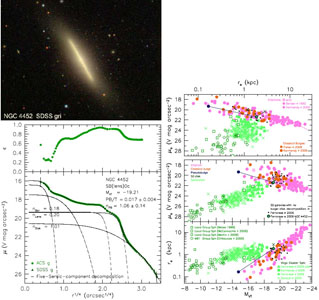 |
Figure 64. (top left) SB(lens)0 galaxy
NGC 4452. The tiny pseudobulge is almost
invisible. The inner disk is
edge-on and very flat; it again consists of two shelves in surface
brightness. Including the outer, thicker disk, these three shelves are
signatures of a bar, lens and disk. (bottom left) Ellipticity є
and surface brightness μV along the major axis of
NGC 4452. The five dashed curves show a
decomposition of the profile
inside the fit range (vertical dashes). The nucleus, bulge, bar, lens
and disk are represented by Sérsic functions with indices n
given in the figure. Their sum (solid curve) fits the data with RMS =
0.044 V mag arcsec-2. (bottom right) Parameter correlations
showing the results of the bulge-disk decomposition. The green filled
circles with the blue centers show the total parameters measured by
Ferrarese et
al. (2006)
for the bulge and disk together. These
points are connected by straight lines to the parameters of the
pseudobulge (blue filled circles) and disk (dark green crosses). From
KB2012. |
The parameter correlations in Figs. 63 and
64 serve to emphasize how
bulge-disk decomposition improves our understanding of the E
sequence. The small black filled dots show the parameters measured by
Ferrarese et al.
(2006)
for the ACS Virgo cluster survey
S0s. They do not violate the E sequence. But they do combine bulge and
disk properties into one set of parameters, so they fail to show
something that is very important. In each of these two galaxies, the
bulge is tiny, comparable in luminosity to the smallest ellipticals. The
classical bulge of NGC 4762 helps to define the extension of the E
sequence toward objects that are more compact than any spheroidal. Even
the tiny pseudobulge of NGC 4452 lies near the compact end of the
E+bulge sequence (cf. Figs. 42
and 43, which show other, similarly
compact and tiny pseudobulges). Figures 68 and
69 will summarize the
parameter correlations for classical bulges and S0 disks,
respectively. Here, I want to emphasize two things. First, there exist
S0 galaxies with classical-bulge-to-total luminosity ratios B /
T that range from almost 1 to essentially zero. The pseudobulge
in NGC 4452 is so small that one cannot hide a
significant classical bulge in that galaxy. Second, both NGC 4762 and NGC 4552 have vertically
thickened and warped outer disks. Both galaxies have nearby
companions.
Kormendy & Bender
(2012)
interpret these results as
indicating that the outer disks are tidally warped and being heated
dynamically in the vertical direction. They present evidence that many
other S0 and Sph galaxies in the Virgo cluster are dynamically heated,
too. Thus NGC 4762 and NGC 4552 are "missing links" that have some
properties of S0 galaxies and some properties of the brightest Sph
galaxies.
NGC 4638 is even more spectacularly an S0 –
Sph transition object. Figure 65 shows (bottom) the
large-scale structure and (top)
an embedded, edge-on disk and bulge in an enlargement from HST
images. When we wrote
KB2012,
this structure was, to our knowledge,
unique. Figure 65 (bottom) suggests that
NGC 4638 is an edge-on S0
whose bulge happens to be very boxy. This would be interesting but not
unique; boxy bulges are discussed in
Section 5.2.9. But already in
the bottom panel of Fig. 65, the structure
looks suspiciously unusual:
the brightness gradient in the boxy structure is very shallow, like that
in its companion, the normal Sph,N galaxy NGC 4637. The top panel of
Fig. 65 shows an almost-round, small bulge in
NGC 4638 with a normal,
steep brightness gradient. To our surprise, the brightness profile
robustly shows (Fig. 66) that the outer
boxy structure has a
Sérsic brightness profile with n = 1.11 ± 0.12
characteristic of the main body of a Sph galaxy. This profile is not
concave-upward, as it would be if the bulge and the boxy structure where
part of the same component with n ≫ 4.
 |
Figure 65. (top) Color image of
NGC 4638 = VCC 1938 made from the HST ACS
g, mean of g and
z, and z images. This image shows the edge-on disk and
central bulge. Brightness is proportional to the square root of
intensity, so the brightness gradient in the bulge is much steeper than
that in the boxy halo. The very red foreground star near the NE side of
the disk is also evident in the bottom image. (bottom) Color image of
NGC 4638 = VCC 1938 from WIKISKY. The
brightness "stretch" emphasizes faint features, i. e., the extremely boxy,
low-surface-brightness halo in which the S0 disk and bulge are
embedded. The elongated dwarf to the west of NGC 4638 is the Sph,N
galaxy NGC 4637. Like many other spheroidals, NGC 4637 is flatter than
any elliptical. Note also that VCC 2048 (not illustrated) is another
"missing link" galaxy with both S0 and Sph properties: like NGC 4637,
it is flatter than any elliptical; its main body is clearly a Sph, but
it contains an embedded, tiny S0 disk (see
KB2012,
from which the above images are taken). |
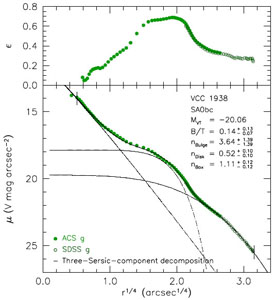 |
Figure 66. Ellipticity є and surface
brightness μV along the major axis of NGC 4638 as
measured on the HST ACS and SDSS g images. Dashed curves
show a three-Sérsic-function decomposition of the profile inside
the fit range (vertical dashes). The bulge is small, but it is
classical. The disk has a Gaussian profile, as do many other S0s
discussed in
KB2012.
Remarkably, the outer, boxy halo is clearly
distinct from the bulge and disk and has a Sérsic index n =
1.11 ± 0.12. The sum of the components (solid curve) fits the
data with an RMS of 0.054 V mag arcsec-2. From
KB2012. |
Kormendy & Bender
(2012)
therefore conclude that NGC 4638
contains three structural components, and edge-on S0 galaxy that
consists of an n = 3.6 ± 1.4 classical bulge plus an
n = 0.5 ± 0.1 Gaussian disk embedded in a normal Sph galaxy
with n = 1.11 ± 0.12. I. e., NGC 4638 has the properties of
both an S0 and a Sph galaxy. VCC 2048 is similar
(Fig. 65 caption).
It is instructive to compare the parameters of the three components of
NGC 4638 with their counterparts in pure S0 and Sph
galaxies (Fig. 67). The classical bulge helps
to define the compact end of the
normal E – Sph parameter sequence. It is within a factor or ~ 2 as
compact as M 32. The disk proves to have the highest effective
brightness of any S0 disk shown in Fig. 69. The
reasons are (1) that
it is edge-on, so the path length through it is large, and (2) that its
profile is Gaussian rather than exponential; the strong outer truncation
results in small re and hence bright
μe. The boxy component is consistent with the
extrapolation of the Sph sequence; it is the brightest Sph galaxy known
in the Virgo cluster.
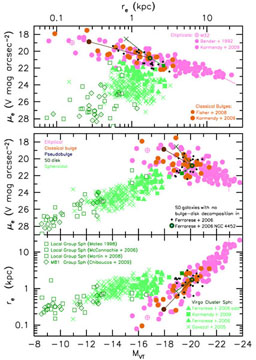 |
Figure 67. Parameter relations showing
results of the bulge-disk-Sph decomposition of NGC 4638. The green
circles with the brown centers show the total parameters measured by
Ferrarese et
al. (2006)
for all components together. These
points are connected by lines to the parameters of the classical bulge
(brown circles), the disk (green crosses), and the Sph halo (green
square). From
KB2012. |
NGC 4638 lives in a high-density part of the Virgo cluster where strong
dynamical heating is plausible. Kormendy & Bender interpret the
boxy Sph part of the galaxy as the dynamically heated remnant of the
outer disk. Because these stars are no longer part of a disk, the disk
that remains has a strongly truncated, i. e., Gaussian profile.
KB2012
discusses additional evidence that higher-luminosity Sphs are, by
and large, more disky. This is consistent with the suggestion that
dynamical heating is one of the S → Sph transformation processes
and that this heating has the smallest effect on the biggest, most
robust galaxies.
7.4.3. Interim summary and road map
In Section 7.4.2, our discussion of the E –
Sph dichotomy branched out in a new direction –
the close relationship between Sphs and S0 galaxy disks.
Section 7.5 pursues this. Meanwhile, it is useful to
summarize where we are.
Section 7 is about environmental secular evolution. The "bottom line"
will be that a variety of environmental processes appear to have
transformed some intermediate-Hubble-type spiral galaxies into S0s and
some late-type spiral and Magellanic irregular (Im) galaxies into
Sphs. Sph galaxies will prove to be bulgeless S0s. "Missing link"
galaxies that have some S0 and some Sph properties are the new subject
that entered the above discussion.
Recall that we were in the process of investigating the E – Sph
dichotomy. That is, even though they look similar, elliptical and
spheroidal galaxies have quantitatively different structural parameters
and parameter correlations. This imples that they have different
formation histories – histories that we are in the process of
deciphering. I reviewed the history of the above discovery,
concentrating on how improved measurements and enlarged galaxy samples
have strengthened the evidence for the dichotomy. Originally not
recognized (Fig. 55), it was first found using
small galaxy samples
(Fig. 57) and since has been confirmed using 90
ellipticals and 295 spheroidals (Fig. 61). Our
next aim has been to add classical bulges,
to increase the sample size and to further show that tiny ellipticals
are not compact because they are tidally stripped. This led us into a
discussion of bulge-disk decomposition and a description of three
example galaxies, two of which have classical bulges that are
substantially as compact as the smallest ellipticals. In our standard
picture of bulge formation by major mergers, these bulges would have
formed before their attendant disks. It is implausible that such bulges
are compact because they were tidally stripped.
The bulge parameters measured and collected in
KB2012 now allow us to
"pay the piper" in confirming our definition of bulges as (essentially)
ellipticals that live in the middle of a disk. This is the subject of
Section 7.4.4. I then return to Sph and S0 galaxies
in Section 7.5.
7.4.4. Classical bulges and ellipticals satisfy the
same fundamental plane parameter correlations. II. Results
Figure 68 shows the parameter correlations from
Fig. 61 with 57 bulges added. Of these, 35 are
known to be classical via their parameters and the discussion in the
source papers (see the key). I also add 22 bulges from
Baggett et al.
(1998);
they are shown with open circles, because we cannot be certain that they
are classical. I examined all of these galaxies and ensured as well as
possible (using Section 5.3) that their
bulges are classical.
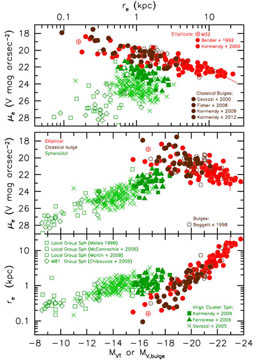 |
Figure 68. Global parameter correlations
from KFCB, from
Kormendy (2009),
and from Fig. 61 here including the sample of
bulges from
KB2012.
All ACS VCS S0s are included, three as Sphs and 23
as bulges. For simplicity, points in further figures encode bulge type
but not the source of the data. |
Figure 68 confirms the assumptions that
underlie our definition of
classical bulges: they satisfy the same parameter correlations as do
ellipticals. Given the uncertainties in bulge-disk decomposition, there
is no evidence that the scatter for classical bulges is different from
that for ellipticals. This is an update of a result that has been found
previously, e. g., by Fisher & Drory
(2008,
2010:
Fig. 41
here). Pseudobulges can satisfy these relations, but they have much
larger scatter, and they fade out by becoming low in surface brightness,
not by becoming compact (Figs. 42
and 43).
7.5. Sph galaxies are bulgeless S0 galaxies
Figure 69 shows
Fig. 68 with the disks of S0 galaxies added.
Kormendy & Bender
(2012)
conclude that spheroidals are continuous in their parameter correlations
with the disks (but not the bulges) of S0
galaxies. People call a galaxy an S0 if it has smooth, nearly elliptical
isophotes and two components,
a bulge and a disk. If it has no bulge and only one,
shallow-surface-brightness-gradient component, we give it a different
name – a spheroidal.
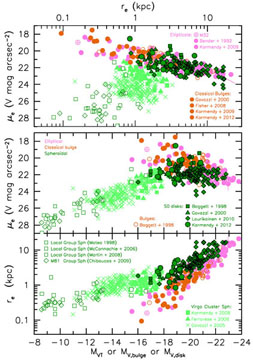 |
Figure 69. Parameter correlations for
ellipticals, bulges and Sphs with disks of 126 S0s added (green points
outlined in black). Bulges and disks of S0 galaxies are plotted
separately. The middle panel shows the
Freeman (1970)
result that disks of big galaxies tend to have the same central surface
brightness μ0 = μe - 1.822
mag arcsec-2 for an exponential.
We conclude that Sphs are continuous with the disks
but not the bulges of S0 galaxies. Updated from
KB2012. |
That bulges disappear where Fig. 69 suggests is
shown in Fig. 70. Rotation curve decompositions
confirm what our experience tells us: bulges disappear at
Vcirc ~ 100 km s-1 or
MV, disk ~ -18
(Tully & Fisher
1977).
There is noise; e. g., M 33
has MV, disk = -19.0 and Vcirc
≃ 135 ± 10 km s-1
(Corbelli 2003)
and no bulge
(Kormendy & McClure
1993).
But of course, we also expect that disks
fade when they are transformed from S+Im to S0.
Figure 70 is an
important observational "target" for future work: the formation physics
that underlies it is largely unknown. But there is ample evidence that
bulges disappear approximately where the Sph and S0 disk sequences meet
in Fig. 69. This is enough to explain the
different names.
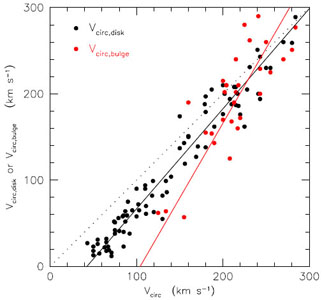 |
Figure 70. Maximum rotation velocity of the
bulge Vcirc,bulge (red points) and disk
Vcirc,disk (black points) derived in
bulge-disk-halo decompositions of the rotation curves of galaxies whose
outer, dark matter rotation velocities are
Vcirc. Equality of the visible and dark
matter rotation velocities is shown by the dotted line. Every red
point has a corresponding black point, but many galaxies are bulgeless
and then only a disk was included in the decomposition. This figure
illustrates the well known rotation curve conspiracy,
Vcirc,bulge ≃
Vcirc,disk ≃
Vcirc for the halo
(Bahcall &
Casertano 1985;
van Albada &
Sancisi 1986;
Sancisi & van
Albada 1987).
It shows that the conspiracy happens mostly for galaxies with
Vcirc ~ 200 km s-1. The lines are
least-squares fits with variables symmetrized around 200 km
s-1. The bulge correlation is steeper than that for disks;
bulges disappear at Vcirc ≃ 104 ±
16 km s-1. From
Kormendy & Bender
(2011)
and
Kormendy & Freeman
(2013). |
Kormendy & Bender
(2012)
suggest that the kink in the μe –
MV correlation that happens roughly at the transition
from S0 disk to Sph tells us where the correlation turns into a sequence
of decreasing baryon retention at lower galaxy luminosity. It is not an
accident that this happens roughly where the bulge contribution to the
gravitational potential well disappears.
7.6. Spiral and irregular galaxies have the same
structural correlations as S0 galaxy disks and Sph galaxies
Kormendy's (1985,
1987)
conclusion that Sph galaxies are defunct dS+Im
galaxies depended critically on the observation
(Fig. 57) that they all
have the same structural parameter correlations. That result was based
on a small number of galaxies and has never been checked.
KB2012 updates
and extends this test with 407 galaxies that cover the complete
luminosity range from the tiniest dwarf irregulars to the brightest Sc
disks. Figure 71 shows that S+Im galaxies do
indeed have the same parameter correlations as S0 disks and spheroidals.
Therefore they are closely related.
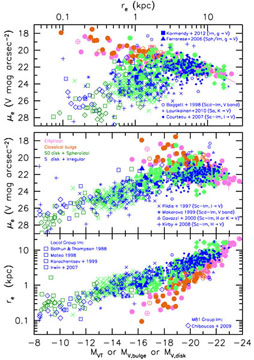 |
Figure 71. Fig. 69
correlations with disks of Sa – Im galaxies added
(blue points for 407 galaxes from 14 sources listed in the keys).
When bulge-disk decomposition is needed, the components are plotted
separately. From
KB2012. |
7.7. A revised parallel-sequence classification of
galaxies
Figure 72 shows our proposed revision of
Sidney van den Bergh's
(1976)
morphological classification scheme based on the
foregoing observations.
Van den Bergh put S0 galaxies in a sequence that parallels the spirals;
the classification parameter that determines the stage along either
sequence is the (pseudo)bulge-to-total luminosity ratio,
(P)B / T. Pseudo and classical bulges are not
distinguished; in a classification based on small-scale images, this is
the only practical strategy. Only (P)B / T and not
parameters such as spiral arm pitch angle determine the stage, so van
den Bergh's classification of spirals is not quite the same as Sandage's
or de Vaucouleurs's. We do not address this issue.
Figure 72 adopts van
den Bergh's theme of placing S0s and spirals in parallel sequences based
only on (P)B / T.
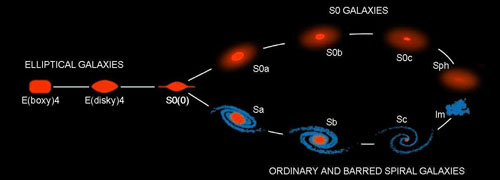 |
Figure 72. Revised parallel-sequence
morphological classification of galaxies. The E types are from
Kormendy & Bender
(1996).
Transition objects between spirals and S0s (van den Bergh's anemic
galaxies) exist but are not illustrated. Bulge-to-total ratios decrease
toward the right; Sc and S0c galaxies have tiny or no
pseudobulges. Sph and Im galaxies are bulgeless. From
KB2012. |
Kormendy & Bender extend ven den Bergh's discussion in two ways.
They resolve the uneasy aspect of van den Bergh's paper that he listed
no S0c or later-type S0 galaxies. Based on a comparison of
(P)B / T ratios of S0s with spirals of known Hubble
type, they find several of the "missing" late-type S0s; e. g., the S0bc
galaxy NGC 4762; the S0c galaxy NGC 4452
(Section 7.4.2).
NGC 4452 is also singled out as an S0c by
Cappellari et al.
(2011),
who independently propose a parallel-sequence
classification based on kinematic maps. A few other S0cs are known
(Laurikainen et
al. 2011;
Buta 2012).
They place Sph galaxies in
parallel with Im galaxies. They note that, in a more detailed
classification that includes Sd and Sm galaxies, some Sphs (e. g., ones
with nuclear star clusters) would be placed in parallel with late-type
(especially Sm) spirals, and others (e. g., ones without nuclei) would
be put in parallel with Ims. Adding Sph galaxies at the late-type end
of the S0 sequence for the first time finds a natural home for them in a
morphological classification scheme.
It is important to understand which observations lead to
Fig. 72
4.
They involve quantitative parameter measurements, but they do not
involve interpretation. First, the
observations that establish E – S0 – Sph continuity:
Galaxies with smooth, nearly elliptical isophotes, little cold gas and
little star formation range in bulge-to-total luminosity ratio from
B / T = 1 to B / T = 0. Here, the existence
of a bulge component and the measurement of B / T are
based on quantitative surface photometry, on nonparametric measurements
of structural parameters for elliptical and Sph galaxies by integrating
the observed isophotes, on parametric (Sérsic-function-based)
bulge-disk decomposition for disk galaxies, and on the resulting
structural parameter correlations
(Figs. 68, 69). When
B / T = 1, we call the object an elliptical; when 1 >
B / T > 0, we call the central component a bulge and
the outer component – if flat
5.
– a disk, and when B / T = 0, we call the galaxy a
spheroidal.
In the structural correlations
between effective radius re, effective brightness
μe ≡ μ(re) and total absolute
magnitude, Sph galaxies define a sequence that is continuous with the
disks but not the bulges of S0 galaxies. There is some overlap in
luminosity between Sphs and S0 disks.
NGC 4762,
NGC 4452, NGC 4638 and VCC 2048 are galaxies that have both S0 and Sph
properties. We know this because all four galaxies are seen edge-on. All
contain flat disks. Three contain a tiny (pseudo)bulge (VCC 2048
contains only a nuclear star cluster). The thick outer components of all
four galaxies have parameters – including Sérsic indices
n ~ 1 – that are indistinguishable from those of Sphs. That
is, these galaxies consist of S0 central parts embedded in Sph or
Sph-like outer halos. This helps to establish S0 – Sph
continuity.
Bigger Sph galaxies tend to be
dynamically more S0-disk-like: they have larger ratios of rotation
velocity to velocity dispersion
(van Zee et al.
2004).
Note: at all L, some Sphs rotate slowly (see
KB2012 for a
review).
These observations justify our conclusion that Sph galaxies are
continuous in their properties with S0 disks, which in turn motivates
our juxtaposition of Sph galaxies with S0cs. In essence, Sph galaxies
are bulgeless S0s.
Observations that suggest parallel sequences of S+Im and S0+Sph galaxies:
For every B / T ratio that is observed in an S0 or Sph
galaxy, there are S or Im galaxies that have corresponding, similar
B / T ratios. We see a continuous transition from S0 to E
as B / T → 0. We do not know whether Sas also have a
continuous transition B / T → 0. The Sombrero galaxy
(NGC 4594) has one of the largest bulge-to-total
ratios known, B / T = 0.93 ± 0.01
(Kormendy & Bender
2013).
I know no Sa with larger B / T. Thus it is prudent to
retain a classification S0(0) that is intermediate between elliptical
and both Sa and S0a.
Except for details such as
spiral structure, the global structure of spirals and S0s is
similar. For any generic Sa, Sb, or Sc galaxy, there are similar S0a,
S0b, or S0c galaxies. In particular, the bulges of spiral and S0
galaxies both satisfy the E parameter correlations. The fractions of
classical and pseudo bulges are similar at similar stages along the
tuning fork
(Kormendy &
Kennicutt 2004).
And the disks of S+Im galaxies have almost the same parameter
correlations as Sph galaxies and S0 disks
(Fig. 71).
Some Sph galaxies contain
low-contrast spiral structure; therefore they contain embedded disks
(Jerjen et al.
2000,
2001;
Barazza et al.
2002;
De Rijcke et al.
2003;
Graham et al.
2003;
Ferrarese et al.
2006;
Lisker et al.
2006,
2007,
2009).
Many dSph companions of our
Galaxy contain intermediate-age stellar populations
(Da Costa 1994;
Mateo 1998:
Fig. 73 here;
Tolstoy et al.
2009).
Both among the Galaxy's satellites and in the larger HST ACS
Nearby Galaxy Treasury Survey
(Weisz et al.
2011a,
b),
dS, dIm and dSph
galaxies have similar, heterogeneous star formation histories except
that the star formation rate in dSph galaxies is currently zero.
This is a matter of definition – if a dwarf contains gas and star
formation, it is called dSph/dIm or dIm. The Virgo cluster contains several examples
(Ferrarese et
al. 2006;
KB2012).
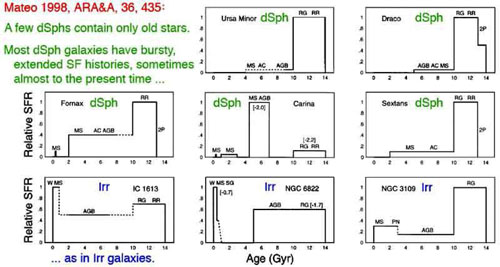 |
Figure 73. Star formation histories of dSph
and dIm galaxies from
Mateo (1998).
Relative star formation rates are shown as a function of time since the
Big Bang. |
Similarly, some spiral
galaxies in clusters contain gas only near their centers, and some S0s
contain near-central gas and small amounts of star formation. This is
discussed in Section 7.9. Here, it again means that
some S0 galaxies are less different from some spiral galaxies than
optical images would suggest.
Van den Bergh's (1976)
"anemic galaxies" are omitted from Fig. 72 for
simplicity, but they are galaxies
that are intermediate in properties between spiral and S0 galaxies.
Their contain only low-amplitude spiral structure star formation. The
transition from S to anemic to S0 looks continuous.
Thus a substantial collection of morphological and structural parameter
observations motivate our suggested parallel-sequence galaxy
classification. We revise it to place Sph galaxies at the end of the S0
sequence, juxtaposed with the latest-type spirals and irregulars. It
is important to note three things. We do not intend to imply that the
luminosity function of galaxies is the same at all stages of the tuning
fork. Indeed, we already know that Im and Sph galaxies tend to have
lower luminosities than earlier-type S and S0 galaxies. Second, we do
not mean to imply that galaxies are equally abundant at every stage of
either the S+Im or the S0+Sph sequence. Indeed, it is clear that S0c
galaxies are much rarer than Sphs or earlier-type S0s. This provides a
hint for interpretation. But it is not a reason to change the
classification. And third, we do not intend to fix what isn't
broken. Our suggestion of a parallel-sequence classification is not
meant to replace Hubble classes. We propose
Fig. 72 as a complement
to Hubble classification, useful because it encodes a different
collection of observations that are relevant to a different collection
of questions about formation physics.
7.8. Parallel-sequence classification and
bimodality in the galaxy color-magnitude relation
Work on galaxy formation nowadays concentrates on the history of star
formation in the Universe and on understanding stellar populations. The
iconic observation that current work tries to explain is the color
bimodality of galaxies in the color-magnitude relation as revealed by
the Sloan Digital Sky Survey (SDSS) at low redshifts
(Strateva et al.
2001;
Bernardi et al.
2003;
Kauffmann et al.
2003a,
b;
Hogg et al.
2002,
2004;
Blanton et al.
2003,
2005;
Baldry et al.
2004)
and by HST studies of galaxies at high
redshifts. Figure 74 shows this result and
illustrates how the E
– S0 – Sph arm of the parallel-sequence tuning fork relates
to it. The bright end of the prominent and thin red sequence consists of
ellipticals, S0s, and some early-type spirals. But their luminosity
functions are bounded at low L. When the red sequence is extended
fainter, it must become dominated by Sphs at MV
≪ -18. The deepest surveys detect this
(Blanton et al.
2005;
Drory et al.
2009).
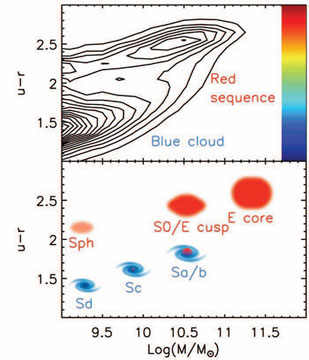 |
Figure 74. Correspondence between our
parallel-sequence classification and the color bimodality of galaxies
in the SDSS color-magnitude relation. The top panel shows contours of
galaxy number density in the correlation between SDSS u -
r color and galaxy baryonic mass M /
M⊙
(Baldry et al.
2004).
The narrow "red sequence" of mostly-non-star-forming galaxies and the
broader "blue cloud" of star-forming galaxies are well known. The
bottom panel shows the morphological types from
Fig. 72 that dominate
in various parts of the top panel. The rapidly rising luminosity
function of spheroidals at the low-mass limit of the diagram may
account for the contour in the top panel at (9.0, 2.2). The "take-home
point" is that the bright end of the red sequence consists of
ellipticals, S0s and early-type spirals, but the faint end is dominated
by Sph galaxies. Adapted from
KB2012. |
7.9. S+Im → S0+Sph galaxy transformation
processes
The natural interpretation of the observations discussed in this section
is that S0 and Sph galaxies are defunct, "red and dead" versions of
spiral and irregular galaxies that have been transformed by physical
processes to be discovered. Most of these turn out to be environmentally
driven and slow.
The relative ordering and positioning of galaxies in the
parallel-sequence classification is justified on purely observational
grounds based on choices of which results to use in the classification
and which to regard – for present purposes – as
secondary. However, it would be disingenuous to pretend that I and many
others have not been thinking about the underlying formation and
evolution processes for a long time. This is inevitable in a world where
no observational curiosity goes uninterpreted for long. In fact, there
are many candidate processes. Astronomers frequently argue about which
of many compelling theories are correct. My experience is that these
arguments go on longest when everybody is correct. This is one of those
occasions.
Candidate S+Im → S0+Sph galaxy transformation processes are
reviewed in
KB2012.
Here, I list them briefly including only the most
important supporting observations:
The main internal evolution process was already mentioned in
Section 7.3. Below a fiducial mass that corresponds
to Vcirc
≃ 100 km s-1, i. e., just where bulges disappear
(Fig. 70) and therefore galaxy names get
changed from S0 to Sph (Fig. 69),
supernova-driven winds are expected to expell a larger
fraction of a galaxy's baryons from lower-mass objects regardless of
whether they now are irregular or spheroidal (e. g.,
Larson 1974;
Saito 1979;
Dekel & Silk 1986;
Vader 1986;
Schaeffer & Silk
1988;
see
Hensler et al.
2004;
Stinson et al.
2007
for two among
many more recent discussions). This is why I suggested that the
decreasing surface brightnesses of Sph and Im galaxies at lower
luminosities (Fig. 71) is a baryon retention
sequence.
The most thoroughly studied
external transformation process is ram-pressure stripping of cold
gas by hot gas in clusters and perhaps groups of galaxies. Suggested by
Gunn & Gott (1972),
the idea has varied in popularity. It has never
gained widespread acceptance, perhaps in part because
Dressler (1980)
argued that it was not the main cause of the morphology-density
relation that spiral galaxies get less abundant whereas S0 galaxies get
more abundant at higher galaxy densities in clusters. Dressler argued
that this result does not strongly depend on cluster richness. However,
examination of his Fig. 8 – 10 (see Fig. 25 in
KB2012)
shows that
the ratio of S0 to S galaxies increases from low-concentration clusters
to high-concentration clusters to X-ray-emitting clusters. An
alternative hypothesis is that ram-pressure stripping happens more
easily in clusters of all richness than simple energy arguments suggest.
More recent results bear this out:
Compelling evidence for
ongoing ram-pressure stripping is provided by Hα and
H i observations of
spiral galaxies in the Virgo cluster
(Chung et al.
2007;
Kenney et al.
2004,
2008).
Figure 75 shows some of these results. Many
spiral galaxies embedded in the X-ray gas that fills the cluster
center show remarkable H i
tails. The above authors interpret them as cold gas that trails behind
the galaxy after having been stripped from the galaxy by the hot gas in
the cluster. The spectacular Hα filaments that point from the
tidally disturbed NGC 4438 toward the hot-gas-rich NGC 4406 (top panel
in Fig. 75) are similarly interpreted as
ram-pressure stripped. Also, many spirals near the center of the cluster
are much smaller and more depleted in
H i than are galaxies in
the cluster outskirts
(Cayatte et al.
1990;
Chung et al.
2009).
Kormendy & Bender
(2012)
note that "the three most depleted galaxies illustrated in Fig. 8 of
Chung et al.
(2009)
are NGC 4402, NGC 4405 and NGC 4064. They have a mean absolute magnitude
MV = -19.4 ± 0.2. Virtually all Sphs are
fainter than this. If even the deep gravitational potential wells of
still-spiral galaxies suffer
H i stripping, then the
shallow potential wells of dS+Im galaxies are more likely to be
stripped." Substantial additional evidence also suggests that
ram-pressure stripping is more effective than we thought (see
KB2012 and
van Gorkom & Kenney
2013
for reviews).
Can ram-pressure stripping
still happen in the Local Group's much shallower gravitational potential
well? Compelling observations which indirectly suggest that the answer
is "yes" are shown in Fig. 76. Close companions
of our Galaxy, of M 31,
and of other nearby giant galaxies are almost all spheroidals; distant
companions are irregulars; Sph/Im transition galaxies tend to live at
intermediate distances, and larger irregulars "survive" at closer
distances to their giant companions
(Einasto et al.
1974;
van den Bergh 1994a,
b,
2007;
Mateo 1998;
Skillman et al.
2003;
Bouchard et al.
2009;
McConnachie 2012).
Hints of similar effects in
larger satellites are seen in the Zurich Environmental Study (ZENS:
Cibinel et al.
2012).
Like previous authors, Kormendy &
Bender suggest that "ram-pressure stripping can happen even in
environments that are gentler than cluster centers. It may be indirect
evidence for a pervasive warm-hot intergalactic medium (WHIM:
Davé et al.
2001)
that is difficult to detect directly but that may be
enough to convert dwarf irregulars into spheroidals."
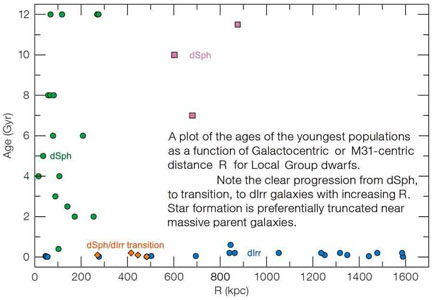 |
Figure 76. From
Mateo (2008),
the ages of the youngest stellar populations in dwarf galaxy companions
versus Galactocentric or M31centric distance R. Except for the
Magellanic Clouds, all close companions
of our Galaxy and of M 31 are spheroidals. Distant companions are
irregulars except for three free-flying dSphs (pink points). The Sph/Im
transition galaxies mostly lie at intermediate distances. |
All this evidence suggests
that ram-pressure stripping is one of the processes that transforms
late-type, gas-rich and star-forming galaxies into red and dead S0 and
Sph galaxies.
Galaxy harassment is a
dynamical process that should operate wherever objects orbit repeatedly
through rapidly varying gravitational potential fields, especially in
virialized clusters of galaxies with velocity dispersions that are much
larger than the internal velocities of galaxies. It is the cumulative
effect of many encounters with other galaxies and with the cluster
potential. Simulations show that it strips outer mass, heats disks and
promotes gas inflow toward the center that presumably feeds star
formation
(Moore et el.
1996,
1998;
Lake et al.
1998).
A variant is tidal stirring of dwarf galaxies on elliptical orbits around
our Galaxy or M 31
(Mayer et al.
2001a,
b,
2006).
Kormendy &
Bender concur with the above authors in suggesting that harassment
converts late-type disks into spheroidals and more robust, earlier-type
spirals into hotter systems that resemble S0s. A benefit of this picture
is that inflowing gas can feed star formation; this helps to explain why
S0 disks and spheroidals – which must fade substantially after
star formations stops – do not have much lower surface
brightnesses than current versions of S+Im progenitors (see
Ferguson & Binggeli
1994
for a review of this problem). Gravity is not
negotiable. Its effects are clean. It is encouraging how many
observations can be tied together into a coherent picture if harassment
is one of the galaxy transformation processes:
Dynamical heating
plausibly explains why faint spheroidals are not flat, why many bright
spheroidals contain disks (either observed directly when seen edge-on or
inferred from their spiral structure), and why the outer parts of our
"rosetta stone" galaxies NGC 4762, NGC 4552, NGC 4638 and VCC 2048 are
vertically thick whereas their more robust inner parts are flat.
Sph and Im galaxies have
similar distributions of axial ratios
(Ferguson & Sandage
1989;
Binggeli & Popescu
1995).
The latter authors conclude that "there
is no evidence for a difference between the flattening distributions of
nucleated dE,N and classical (giant) Es". However, in my
experience, many Sph,N galaxies are flatter than any elliptical.
NGC 4637 in Fig. 65 and VCC 2048 in Fig. 10 of
KB2012 are
examples. Ferguson & Sandage note that "The similarity of
flattenings of dE (bright, no N) and Im types removes one of the
previous objections to the hypothesis that some dwarf ellipticals could
be stripped dI's". The exact engineering needs further study, but
dynamical heating added to the fact that the smallest galaxies are not
flat anyway provides a promising way to explain the flattening
observations.
Intracluster light is
believed to consist of stars that have been stripped by harassment from
individual galaxies. In the Virgo cluster, it is irregular and still in
the early stages of formation
(Mihos et al.
2005,
2009;
Arnaboldi et al.
1996,
2002,
2004;
Castro-Rodriguéz
et al. 2009;
Arnaboldi & Gerhard
2010).
In rich clusters, it is widely observed
(Thuan & Kormendy
1977;
Adami et al. 2005;
Krick & Bernstein
2007;
Gonzalez et al.
2007;
Okamura 2011).
When intracluster light is very bright, it is called a "cD halo"
(Morgan & Lesh
1965;
Oemler 1976;
Schombert 1988).
These halos are robustly understood to consist
of tidally liberated stars and disrupted galaxies
(Richstone 1976;
Dressler 1979;
Kelson et al.
2002).
If gravitational harassment
can produce all these effects, it is difficult to see how the mere
heating of smaller galaxies could be avoided.
Kormendy & Bender
(2012)
suggest that the "new class of dwarfs that are of huge size (10000 pc in
diameter in the extreme) and of very low surface brightness of about 25
B mag arcsec-2 at the center" discovered by
Sandage & Binggeli
(1984)
are "spheroidals that have been harassed almost to death".
Anisotropic dynamical
heating is a natural way to try to explain triaxial and slowly rotating
Sphs (e. g.,
Bender & Nieto
1990).
This idea is consistent with the
observation that the brightest Sphs are in many cases the most disky and
rapidly rotating ones. However, unusually violent encounter histories
can allow a small number of Sphs to be anisotropic even at the highest
masses.
Carefully engineered
encounter histories can make Sph galaxies that have kinematically
decoupled subsystems, even counterrotation of the harassed outer parts
with respect to the inner galaxy
(De Rijcke et
al. 2004;
González-García et al. 2005).
Counterrotating systems are seen in VCC 510
(Thomas et al.
2006).
Starvation of continued infall
of cold gas from the cosmological structure hierarchy is frequently
discussed as an S+Im → S0+Sph transformation process (e. g.,
Larson et al.
1980;
Balogh et al.
2000;
Bekki et al.
2002;
Boselli et al.
2009).
Absent such infall, star formation at currently observed rates generally
uses up the available gas in a few Gyr
(Larson et al.
1980;
Boselli et al.
2009).
Given the observation that the center of the Virgo cluster and a
fortiori the centers of rich clusters of galaxies are dominated by
hot gas (e. g., Fig. 75), it is difficult to
see how starvation can be avoided. These are not environments where
low-density cold gas can survive to feed continued accretion onto
galaxies for billions of years after the cluster acquires a large
velocity dispersion.
Thus many processes (1) may explain the growing dark matter dominance
(i. e., baryon deficiency) of lower-mass dwarf galaxies and (2) can
potentially transfrom S+Im galaxies into S0+Sph galaxies.
Kormendy & Bender
(2012)
emphasize that "the relevant question is not `Which
one of these mechanisms is correct?' It is `How can you stop any of them
from happening?' It seems likely to us that all of the above processes
matter."
In this regard, I conclude by emphasizing the following points.
Most papers
(Boselli et al.
2009
is an exception) investigate one
process; when they get into trouble explaining some particular
observation, they conclude that this process is not the answer. If all
above processes happen, then there is more potential to understand all
of the diagnostic observations. Theorists like to ask clean questions,
investigating one process at a time. There are good reasons for
this. But Nature does everything together. Eventually, we will have to
do likewise if we expect to understand galaxy evolution. The hellishly
complicated interplay of different processes is a feature, not a bug. We
cannot avoid this problem forever.
Second, one observation that is frequently cited to disfavor
ram-pressure stripping and strangulation is that bulges are
systematically bigger in S0s than in spirals (e. g.,
Dressler 1980).
But (i) small pseudobulges in late-type spirals skew the distribution of
S-galaxy bulges to smaller luminosities; if such galaxies are
transformed before secular evolution has time to make pseudobulges, the
result is a Sph, not an S0. Then it will not be counted among the
S0s. Also, (ii) the distribution of S0 bulges is skewed toward high
luminosity by the frequent misclassification of the highest ellipticals
as S0s (KFCB).
This happens because their high Sérsic indices
n ≫ 4 give them a "core-halo" appearance that persuades
classifiers to call them S0s. An example is the elliptical galaxy
NGC 4406, which is classified S0 by
Sandage & Tammann
(1981).
Similarly, giant ellipticals are commonly classified S03 when
they contain nuclear dust disks; e. g., the elliptical NGC 4459
(KFCB).
(iii) When accurate bulge-disk decompositions are carried out,
the folklore that S0 galaxies mostly have large bulges is not
confirmed. Among S0s discussed in
KFCB and in
KB2012, about half have
(P)B / T < 0.5 and six have (P)B /
T  1/3, the
value for the Sb galaxy M 31. Finally, (iv) the distribution of
B / T in the progenitor galaxies of any transformation
process is a strong function of environment – bulgeless disks are
preferentially made in the field, and merger remnants are preferentially
made in clusters such as Virgo
(Kormendy et al.
2010).
So field spirals do not fairly sample the potential progenitors of S0
galaxies in clusters.
1/3, the
value for the Sb galaxy M 31. Finally, (iv) the distribution of
B / T in the progenitor galaxies of any transformation
process is a strong function of environment – bulgeless disks are
preferentially made in the field, and merger remnants are preferentially
made in clusters such as Virgo
(Kormendy et al.
2010).
So field spirals do not fairly sample the potential progenitors of S0
galaxies in clusters.
Another observation that is frequently cited to disfavor ram-pressure
stripping and strangulation is that S0s have higher surface brightnesses
than spirals. Disk fading that follows the shutdown of star formation
might lead us to expect the opposite effect. But
Fig. 71 shows little
sign of such an effect. Note that the surface brightnesses of both S0
and spiral disks are not corrected for inclination, so they are treated
in the same way. However, internal absorption is important in spirals
and not in S0s. So internal-absorption-corrected surface brightnesses of
spiral galaxy disks would be brighter than those of S0 disks. Also,
harassment – like any effect that rearranges angular momentum
– persuades some gas to fall toward the center and should increase
the surface brightness there via star formation.
Finally,
Kormendy & Bender
(2012)
point out that S → S0
transformation does not require the removal of all gas nor the quenching
of all star formation. Some S0s still contain gas, especially molecular
gas near their centers (e. g.,
Welch & Sage 2003;
Sage & Wrobel 1989;
Thronson et al.
1989;
Devereux & Young
1991;
Young et al.
1995).
These S0s form stars. The Virgo spirals whose
outer H i distributions are
truncated have normal central molecular gas content
(Kenney & Young
1986).
We do not need to solve the problem of removing all gas from the
deepest parts of galaxy potential wells.
It is clear that much work – much complicated work –
is still needed on the messy baryonic physics of galaxy evolution. But I
am encouraged to think that the still unknown details of the various
transformation processes do not threaten our overall picture that at
least some S0s and likely all Sph galaxies are defunct spiral and
irregular galaxies.
7.10. Environmental secular evolution –
"An Idea Whose Time Has Come"
Morphological observations such as those encoded in the
parallel-sequence classification of Fig. 72
lead to the robust
conclusion that many S0s are closely related to spiral galaxies and that
essentially all Sph galaxies are closely related to the latest-type
spirals and irregulars. Figure 72 does not
directly tell us what that
relationship is. However, in recent years, rapidly improving
observations of transformation processes in action, including
H i and Hα tails,
relatively
recent star formation in dSph galaxies, vertically thick outer disks in
interacting S0s and "rosetta stone" galaxies with both S0 and Sph
properties, strongly imply that some or all of a collection of
environmental processes transform spiral and irregular galaxies into red
and dead S0 and spheroidal galaxies. This happens especially in rich
clusters, but small galaxies can suffer transformation even in
relatively quiescent environments such as the Local Group.
Kormendy & Bender
(2012)
suggest that "environmental secular evolution is An
Idea Whose Time Has Come."
4
Allan Sandage (2004)
accused Sidney van
den Bergh of hermeneutical circularity in setting up his
parallel-sequence classification, which – he thought –
involved too much interpretation. A prosaic but sufficient paraphrase is
"circular reasoning". The basic idea is this: a morphological
classification of galaxies should be set up based only on observations
and not on interpretation (see
Section 3.4). The aim is that
regularities revealed by the classification will later aid
interpretation. However, if some interpretation is used in setting up
the classification, then the "aid" that the classification can provide
is foreordained. This is circular reasoning. In practice, science is not
as "black and white" as Sandage suggests. Even the greatest scientists
(Sandage explicitly picked Hubble as one of these) set up
classifications with future interpretation in mind. They make decisions
about which observations to treat as relevant and which ones to treat as
secondary. Van den Bergh did this faithfully; Sandage was just uneasy
about how important those decisions were. It should be clear from these
remarks that I respect both sides of the argument. In the end, further
advances reviewed here have, I claim, vindicated van den Bergh's
decisions. For a classification to be successful, it must ultimately
motivate a clearcut paradigm of interpretation. Van den Bergh's
parallel-sequence classification has done this.
Back.
5 This
is to prevent confusion with cD galaxies, which have cluster-sized
debris halos, not disks.
Back.











 MB
MB
 -15, both
structural classes of elliptical galaxies coexist"
(Wirth & Gallagher
1984).
This implies that the luminosity functions of elliptical and spheroidal
galaxies differ as shown in Fig. 56.
-15, both
structural classes of elliptical galaxies coexist"
(Wirth & Gallagher
1984).
This implies that the luminosity functions of elliptical and spheroidal
galaxies differ as shown in Fig. 56.



















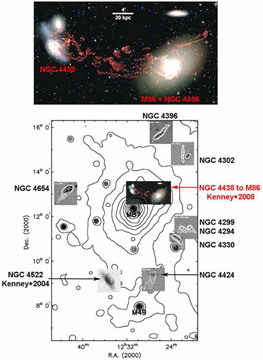

 1/3, the
value for the Sb galaxy M 31. Finally, (iv) the distribution of
B / T in the progenitor galaxies of any transformation
process is a strong function of environment – bulgeless disks are
preferentially made in the field, and merger remnants are preferentially
made in clusters such as Virgo
(Kormendy et al.
2010).
So field spirals do not fairly sample the potential progenitors of S0
galaxies in clusters.
1/3, the
value for the Sb galaxy M 31. Finally, (iv) the distribution of
B / T in the progenitor galaxies of any transformation
process is a strong function of environment – bulgeless disks are
preferentially made in the field, and merger remnants are preferentially
made in clusters such as Virgo
(Kormendy et al.
2010).
So field spirals do not fairly sample the potential progenitors of S0
galaxies in clusters.