


In February of 1982, Mordehai Milgrom submitted a trio papers to the Astrophysical Journal [214, 215, 216]. These papers, which Milgrom developed at the Weizmann Institute in Israel and while on sabbatical at Princeton's Institute of Advanced Study, provided the foundation for what would become the leading alternative to dark matter. This proposal, known as Modified Newtonian Dynamics, or MOND, was a seemingly simple one, but with extremely far reaching consequences. At the heart of MOND is the recognition that if instead of obeying Newton's second law, F=ma, the force due to gravity scaled as F = m a2 / a0 in the limit of very low accelerations (a ≪ a0 ∼ 1.2 × 10−10 m/s2), then it would be possible to account for the observed motions of stars and gas within galaxies without postulating the presence of any dark or otherwise hidden matter. In Milgrom's proposal, there was no dark matter. Instead, what astronomers had discovered was evidence of a new framework for gravity and dynamics, beyond that described by Newtonian physics or even by general relativity.
A. Toward a Realistic Theory of MOND
Milgrom's initial proposal was not intended to represent a realistic theory, but rather was presented as the approximate weak-field limit of some unknown, but more complete framework. In its original form, it was not even clear whether MOND was merely a modification of the behavior of gravity, or was instead a more general correction to Newton's second law, applicable to all forces. Within the context of either interpretation, however, it has proven challenging to embed MOND-like behavior within a realistic theoretical framework. First of all, in its original formalism, MOND does not conserve momentum, angular momentum, or energy. Furthermore, Milgrom did not initially propose any means by which MOND could be embedded within a theory consistent with general relativity. Before MOND could be considered a viable alternative to dark matter, a more realistic version of this theory would have to be developed. And while significant progress has been made toward this goal over the past three decades, this progress has often been accomplished at great expense in terms of economy and simplicity.
A first step in this direction was made in 1984 through the collaboration of Milgrom with Jacob Bekenstein, and their proposal of the AQUAdratic Lagrangian theory (AQUAL) [38]. In AQUAL, Bekenstein and Milgrom began with a modification of the Lagrangian of Newtonian gravity, rather than with a modification of Newton's second law. As a result, this approach automatically preserves the conservation of momentum, angular momentum, and energy, and respects the weak equivalence principle. And while the predictions of AQUAL are identical to those of MOND only in special and highly symmetric cases, the differences between the predictions of these two theories are typically modest (at the ∼10% level) [217].
Despite its advantages over the original version of MOND, AQUAL was still a modification of Newtonian dynamics, and is not compatible with the general theory of relativity. In order for any variation of MOND to be taken seriously, it would need to be able to account for the many varieties of relativistic phenomena that have been observed, including those of gravitational lensing and cosmological expansion. The first attempts to embed MOND into a relativistic framework involved theories with more than one metric. In relativistic AQUAL (RAQUAL) [38], for example, the dynamics of matter and radiation are dictated by a metric that is distinct from the standard spacetime metric that applies to the gravitational field. The difference between these two metrics is the result of the presence of an additional scalar field which, along with matter, contributes to the gravitational potential. In this respect, RAQUAL shares some of the features of much earlier scalar-tensor theories of gravity [169, 63]. To avoid causal problems resulting from the superluminal motion of the scalar field, however, RAQUAL had to be further modified [37], and these changes were to the detriment of the theory's consistency with precision solar system tests. Even more problematic was the fact that these early attempts at a relativistic theory of MOND failed to adequately describe the phenomena of gravitational lensing.
Although the deflection of light is predicted to occur in RAQUAL and other relativistic formulations of MOND, the magnitude of such lensing is generally expected to be proportional to the amount of (baryonic) mass that is present in the deflecting system. In contrast, the degree of lensing that is observed around galaxy clusters is much larger than can be accounted for by the mass of the baryons alone. In this respect, RAQUAL cannot address the dark matter problem on cluster scales.
Although other efforts to resolve this issue were attempted [40, 274], it was not until 2004 that Bekenstein proposed the first realistic solution to the problem of gravitational lensing in relativistic theories of MOND [39]. Since its proposal, Bekenstein's TeVeS theory – short for Tensor-Vector-Scalar gravity – has become the leading theory of MOND, and has received a great deal of attention. Beyond those of general relativity, TeVeS contains two additional fields, three free parameters, and one free function. On the one hand, this freedom makes TeVeS somewhat limited in its predictive power. On the other, it provides TeVeS with enough flexibility to potentially be consistent with gravitational lensing observations and other cosmological considerations, such as those pertaining to structure formation and the cosmic microwave background.
B. Observational Successes and Failures
Early in its history, it was appreciated that MOND was capable of explaining the observed dynamics of many spiral and elliptical galaxies. MOND also, however, made predictions for the behavior of low surface brightness galaxies, whose dynamics had not yet been well measured. The fact that such systems were later found to be compatible with MOND [75, 208] served to bolster interest in the theory. Today, MOND appears to be compatible with the observed rotations curves of hundreds of spiral galaxies [36, 273, 218, 219].
In addition to galactic rotation curves, MOND also provides an explanation for the empirical Tully-Fisher formula [311], which relates the intrinsic luminosities and rotational velocities of spiral galaxies, L ∝ Vrotα, where α ≈ 4. If one assumes a common mass-to-light ratio for all galaxies, MOND predicts precisely this relationship, with a value of α = 4, which is consistent with observations [209].
On the scale of galaxy clusters, MOND has not been nearly as successful. While MOND does reduce the need for additional mass in clusters, significant quantities of dark matter are still required. If the three known species of neutrinos were as heavy as mν ∼ 1-2 eV (near the upper limits from beta decay experiments), it has been suggested that they might be able to account for this discrepancy, essentially acting as dark matter in clusters [275, 26, 276]. Massive neutrinos can also help to reduce to some degree the discrepancy between measurements of the cosmic microwave background and the predictions of TeVeS [295].
In recent years, the debate over MOND has been focused on the use of gravitational lensing to measure the mass profiles of galaxy clusters. The idea that lensing could be used to determine the mass of a galaxy or a galaxy cluster was first proposed by Fritz Zwicky in his famous paper of 1937 (see Chapter III A). It was more than 40 years later that the first gravitational lens was observed [324] – two mirror images of a quasar – and another decade after that before the first observations were made of lensing by a galaxy cluster [204, 299]. Today, gravitational lensing is frequently used to study the properties of clusters (see e.g. Refs. [155, 211] for recent reviews).
In 2006, a group of astronomers including Douglas Clowe transformed the debate between dark matter and MOND with the publication of an article entitled, “A direct empirical proof of the existence of dark matter”. In this paper, the authors described the observations of a pair of merging clusters collectively known as the “bullet cluster” (and also known as 1E0657-558) [81]. As a result of the clusters' recent collision, the distribution of stars and galaxies is spatially separated from the hot X-ray emitting gas (which constitutes the majority of the baryonic mass in this system). A comparison of the weak lensing and X-ray maps of the bullet cluster clearly reveals that the mass in this system does not trace the distribution of baryons (see Fig. 7). Another source of gravitational potential, such as that provided by dark matter, must instead dominate the mass of this system.
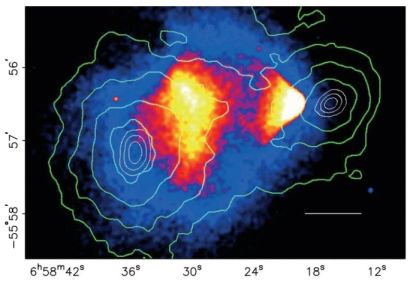 |
Figure 7. The bullet cluster. The colored map represents the X-ray image of this system of merging clusters, obtained in a 500 second exposure with Chandra. The white bar is shown for scale, and represents a distance of 200 kpc at the location of the cluster. The green contours denote the reconstructed lensing signal, proportional to the projected mass in the system. From Ref. [81]. |
Following these observations of the bullet cluster (and of other similar systems), many researchers expected that this would effectively bring the MOND hypothesis to an end. In the years since, however, anything but has taken place. Since the introduction of TeVeS, MOND has continued to attract a great deal of attention, despite its failure to address the dynamics of galaxy clusters, and in particular the bullet cluster. In addition to massive neutrinos, some authors have considered the possibility that TeVeS's vector field might source the gravitational potential of the bullet cluster, itself acting much like dark matter on cluster scales. Similarly, the failure of TeVeS to predict the observed ratio of the second and third peaks of the cosmic microwave background's angular power spectrum might be plausibly averted if some of TeVeS's additional degrees-of-freedom behaved much like cold dark matter during the early history of the Universe. And although this possibility goes somewhat against the original spirit of MOND, it is hard to rule out at this time. Taken together, the bullet cluster and other increasingly precise cosmological measurements have been difficult to reconcile with all proposed versions of MOND, and it remains unclear whether TeVeS, in some form, might be compatible with these observations [295, 97, 293]. For reviews, See Refs. [294, 116].