


7.1. The Formation of Ultra-Faint Dwarfs and the Stellar Mass-Halo Mass Relation
The formation of the first galaxies depends critically on the mechanisms that allow gas to cool to low enough temperatures for star formation to begin (see, e.g., Bromm & Yoshida (2011) and references therein). UFDs may form either in dark matter minihalos of 106 − 108 M⊙ (e.g., Bovill & Ricotti, 2009, Salvadori & Ferrara, 2009), which cool via molecular hydrogen and are thought to be the hosts of the first Population III stars at z∼ 20, or in atomic cooling halos of > 108 M⊙, which cool initially via atomic hydrogen lines and collapse later at z∼ 10 (e.g., Li, De Lucia & Helmi, 2010, Frebel & Bromm, 2012). Observationally, it may be possible to distinguish these scenarios via either the present-day halo masses of UFDs or their chemical enrichment.
Simulating such tiny galaxies is a difficult computational problem because of the high resolution and high dynamic range needed. There are at least three approaches used in the literature to study small dwarf galaxies theoretically. First, one can directly carry out ultra-high resolution zoom-in simulations of the first galaxies, which explore the physics of the formation and evolution of such systems, but the simulations are generally too expensive to run to the present day (e.g., Wise et al., 2014, Jeon et al., 2015). Alternatively, simulations of dwarf galaxies located in isolated environments can be run to z = 0, at the cost of missing the physics associated with satellite dynamics and stripping (e.g., Simpson et al., 2013, Wheeler et al., 2015). Finally, simulations of satellites of Milky Way-like galaxies may include all of the relevant physics and run to z = 0, but are only just beginning to reach the resolution required to study UFDs (e.g., Wetzel et al., 2016, Garrison-Kimmel et al., 2018). In the latter two classes of simulations the properties of the simulated dwarfs are typically in reasonable agreement with observations (e.g., Wetzel et al., 2016, Jeon, Besla & Bromm, 2017), but more computing power and higher resolution will be needed to investigate the formation of ultra-faint dwarfs in detail.
One of the most basic questions regarding the formation of dwarf galaxies in a cosmological context is what dark matter halos they occupy. The properties of their dark matter halos control when dwarfs form, their gas content, and their resilience to heating by stellar feedback and reionization. The correspondence between galaxy stellar masses and dark matter halo masses is referred to as the stellar mass-halo mass (SMHM) relation. As emphasized by Buckley & Peter (2017) and Kim, Peter & Hargis (2017), the SMHM relation is the key to understanding most of the so-called small scale challenges to the ΛCDM model (e.g., Bullock & Boylan-Kolchin, 2017).
For halo masses below ∼ 1012 M⊙, the SMHM relation is generally described as a power law, M* ∝ Mhaloα with small scatter (Moster, Naab & White, 2013, Behroozi, Wechsler & Conroy, 2013). How the relation behaves for stellar masses below ∼ 107 M⊙(i.e., for classical and ultra-faint dwarfs) is currently a matter of debate. Hydrodynamic simulations suggest very large scatter at these lowest masses, with an increasing fraction of halos remaining completely dark (e.g., Shen et al., 2014, Sawala et al., 2016, Munshi et al., 2017). However, Jethwa, Erkal & Belokurov (2018) argued based on Bayesian fits to the Milky Way satellite LF with a wide variety of SMHM parameterizations that the observational data are matched better without large scatter, and that the fraction of halos hosting observable galaxies must be significant even at quite low masses. Alternatively, Read & Erkal (2018) recently proposed that a relation between the mean star formation rate and halo mass may be better constrained at dwarf galaxy masses than the SMHM relation is. The discovery of additional satellites and completeness analyses of surveys beyond SDSS will offer improved constraints on the matching between halos and UFDs, which may provide the solution to the missing satellite problem (Kim, Peter & Hargis, 2017, Read & Erkal, 2018).
The orbits of dwarf galaxies around the Milky Way control both their tidal evolution and potentially their gas loss through ram-pressure stripping or other effects. However, without three-dimensional kinematic information, only weak orbital constraints are possible. By comparing radial velocity measurements with the Via Lactea II N-body simulation, Rocha, Peter & Bullock (2012) were able to determine approximately when the classical and SDSS satellites last crossed the virial radius of the Milky Way, but the specific orbits of each dwarf remained unknown. For the 15 UFD candidates that lack radial velocities (Section 2), even the infall times cannot be measured.
Until very recently, the only published proper motion for a UFD was the ground-based measurement for Segue 1 (the closest dwarf) by Fritz et al. (2018b). However, the situation changed dramatically as soon as the second data release (DR2) from Gaia became available. Gaia Collaboration et al. (2018) measured the proper motion and orbit of Boo I, and Simon (2018), Fritz et al. (2018a), and Kallivayalil et al. (2018) immediately determined the proper motions and orbits of all UFDs for which spectroscopic members were available. At magnitude G = 16, 17, 18, and 19, Gaia DR2 provides typical proper motion uncertainties of 0.09, 0.15, 0.26, and 0.51 mas yr−1, respectively (Lindegren et al., 2018), so even a single UFD member star brighter than G ≈ 18 is sufficient to determine an accurate proper motion for a given galaxy. The corresponding tangential velocity uncertainties are 43, 71, 123, and 241 (d/100 kpc) km s−1, where d is the distance in kpc. By averaging the proper motions of multiple members, smaller uncertainties can be achieved. Remarkably, the Gaia astrometry is so accurate that UFD proper motions can be measured with a combined photometric and astrometric selection even without any spectroscopic membership information (Massari & Helmi, 2018, Pace & Li, 2018). We are therefore suddenly in the situation where UFD proper motions outnumber radial velocities. For UFDs beyond ∼ 150 kpc, the Gaia DR2 proper motions are generally consistent with zero, but that can be improved by the identification of additional member stars and by future Gaia releases.
Orbits based on full six-dimensional phase space information have now been computed for all of the Milky Way’s ultra-faint satellites with known radial velocities (Gaia Collaboration et al., 2018, Simon, 2018, Fritz et al., 2018a, Kallivayalil et al., 2018). The most important orbital parameter is the pericenter distance, which fortunately only depends rather weakly on the assumed gravitational potential of the Milky Way. For the satellites within 100 kpc, the median pericenter is 38 kpc, the pericenter is generally determined to within 10−20%, and the typical orbital period is several Gyr (Simon, 2018, Fritz et al., 2018b). Surprisingly, this orbit modeling reveals that nearly all of the closest dwarfs are currently very close to the pericenters of their orbits. Only Boo I, Willman 1, and Tucana II are more than ∼ 5 kpc beyond their pericenter distances (Simon, 2018). The most natural explanation for this peculiar positioning is that there is a selection bias against discovering UFDs that are far from their orbital pericenters. If that is the case, then most of the dwarfs found in SDSS, DES, and other surveys must be close to the survey detection limits, as suggested by Koposov et al. (2008), but contrary to the results of Walsh, Willman & Jerjen (2009), Bechtol et al. (2015), and Drlica-Wagner et al. (2015). Deeper surveys should then reveal a significantly larger population of UFDs that are distributed more evenly along their orbits.
The satellites discovered in DES imaging are noticeably concentrated around the Large and Small Magellanic Clouds (Bechtol et al., 2015, Drlica-Wagner et al., 2015). This result led to speculation that many of these objects might have originated as Magellanic satellites and are now being accreted by the Milky Way (Deason et al., 2015, Drlica-Wagner et al., 2015, Jethwa, Erkal & Belokurov, 2016, Sales et al., 2017), as originally predicted by D’Onghia & Lake (2008). Based on their space motions and orbits, the most likely dwarfs to have formed in the Magellanic group are Horologium I, Hyi I, Carina III, and Tucana II (Kallivayalil et al., 2018, Simon, 2018).
Since their discovery, it has frequently been suggested that many UFDs are experiencing significant tidal stripping as they orbit the Milky Way (e.g., Belokurov et al., 2006, Zucker et al., 2006a, Niederste-Ostholt et al., 2009, Muñoz, Geha & Willman, 2010, Sand et al., 2012, Kirby et al., 2013a, Roderick et al., 2015, Collins et al., 2017, Simon et al., 2017). The objects upon which this speculation has focused include Hercules, Leo V, UMa I, UMa II, Segue 1, Segue 2, and Tuc III. The physical reasoning supporting the idea of tidal stripping or tidal disruption for these satellites ranges from morphology (highly elongated shapes; Hercules and UMa I), apparent extratidal features (Hercules, Segue 1, and Tuc III), and possible velocity gradients (Hercules and Leo V) to deviations from the luminosity-metallicity relation (Segue 2).
Now that the orbits of the UFDs are known, the possibility of tidal stripping or tidal disruption can be discussed much more quantitatively. While some stripping of the dark matter from satellite galaxies is inevitable on almost any orbit, they must approach the Milky Way much more closely in order for an appreciable fraction of their stars to be lost (Peñarrubia, Navarro & McConnachie, 2008). The tidal radius of a dwarf galaxy is unfortunately not a well-defined quantity, as it varies with time and depends on both the poorly-known mass distribution of the Milky Way and the even more poorly-known mass distribution of the dwarf. In lieu of carrying out detailed numerical experiments for each dwarf, one can approximate the tidal radius as the Jacobi radius (Binney & Tremaine, 2008):
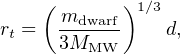 |
(3) |
where mdwarf is the mass of the dwarf galaxy, MMW is the mass of the Milky Way interior to the location of the dwarf, and d is the distance of the dwarf from the Galactic center. However, we also encourage future computational work to model the response of stars within a dwarf to a time-variable external tidal field in a more realistic way.
To conservatively assess stripping, we adopt a heavy (1.6 × 1012 M⊙) Milky Way model and assume that the total mass of each dwarf is limited to the measured mass within its half-light radius. Since the actual halo mass of a dwarf is expected to be several orders of magnitude larger in the absence of stripping, this scenario places a lower bound on the tidal radius. Under these assumptions, we calculate that the tidal radius is currently beyond 3 R1/2 for all of the UFDs except Tuc III (rt = 2.3 R1/2) and UMa I (rt = 2.2 R1/2). The former is not surprising, as Tuc III has an orbital pericenter of only ∼ 3 kpc (Erkal et al., 2018, Simon, 2018, Fritz et al., 2018b), at which point its tidal radius may be smaller than its present half-light radius. Not coincidentally, Tuc III is also the only UFD that is unambiguously suffering substantial stripping, with clear tidal tails comprising the majority of its stellar mass extending at least 1 kpc from its main body (Drlica-Wagner et al., 2015, Shipp et al., 2018, Li et al., 2018a, Erkal et al., 2018). UMa I, on the other hand, has a pericenter of ≈ 101 kpc (Simon, 2018, Fritz et al., 2018b), essentially equal to its current distance. Its tidal radius is therefore at its minimum value now, and the outer ∼ 15−20% of its stars may be vulnerable to stripping. Recall, however, that we have made the extreme assumption that the dark matter halo of each dwarf is truncated at its half-light radius. If the halo of UMa I is substantially more extended, as is very likely to be the case, then only minimal stripping of its stars is possible.
For the remaining UFDs with published kinematics, significant stripping generally appears unlikely. At the pericenters of their orbits, Hyi I and Boo I each have rt ≈ 3 R1/2, which would leave ≈10% of their stars unbound. Again, though, more realistic assumptions about the mass and extent of their dark halos would result in no significant stellar stripping. Segue 2 is in danger of stripping if its velocity dispersion is much smaller than the upper limit determined by Kirby et al. (2013a). If σ ≲ 0.7 km s−1, then its tidal radius would be ≈ 2 R1/2 at pericenter, so tides remain a plausible explanation for its offset from the luminosity-metallicity relation. The more distant dwarfs often regarded as likely to have been stripped or disrupted, Hercules and Leo V, can only experience tidal stripping if they are on extremely eccentric orbits bringing them within 10−20 kpc of the Galactic center. Such an orbit is not currently excluded for Hercules, but is unlikely for Leo V (Fritz et al., 2018b). With larger halo masses these dwarfs would need to pass within a few kpc of the Milky Way to be disrupted. We therefore suggest that alternative explanations for elongated shapes and velocity gradients, such as formation through mergers or puffy disks (e.g., Starkenburg, Helmi & Sales, 2016, Wheeler et al., 2017), should be considered before necessarily attributing such properties to Milky Way tides.