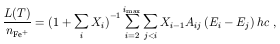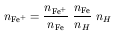4.5. Testcase #5
In this example we illustrate how PopRatio may be used to calculate the cooling rate due to collisional excitation of low-lying levels of a given atom or ion.
As an example we take the ion Fe+, because iron is an astrophysically abundant element. The ion Fe+ may be the dominating ionization stage in low ionization regions, and may be an important gas coolant [30].
The cooling rate is given by [4]:
Rewriting this in terms of the total Fe+ density
nFe+ =
with the energies Ei expressed in cm-1. The
Fe+ density will depend on its
fractional abundance and on the iron elemental abundance:
Here we calculate the cooling function, defined as the right hand
side of eq. (26).
Since Fe+ has a complicated electronic structure,
several levels must be taken into account in the calculation. We employ
a 16-level model ion,
allowing us to calculate the cooling function for electronic densities
as high as 104 cm-3.
To run this testcase the user does not need to modify function URAD,
since no fluorescence
transitions are loaded in.
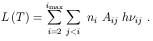
 i ni
and the population ratios
Xi = ni+1 / n1:
i ni
and the population ratios
Xi = ni+1 / n1: