

| © CAMBRIDGE UNIVERSITY PRESS 2000 |
7.1 Observations of large-scale structure
As we look out into the sky, it is quite clear that galaxies are not spread uniformly through space, but are clumped into groups and rich clusters. Figure 7.1 shows the positions on the sky of almost 15 000 bright galaxies, taken from three different catalogues compiled from optical photographs. Very few of them are seen close to the plane of the Milky Way's disk at b = 0, and this region is sometimes called the Zone of Avoidance. The term is unfair: surveys in the 21 cm line of neutral hydrogen, and in far-infrared light, show that galaxies are indeed present, but their visible light is obscured by dust in the Milky Way's disk. Dense areas on the map mark rich clusters: the Virgo cluster is close to the north Galactic pole, at b = 90°. Few galaxies are seen in the Local Void, stretching from l = 40°, b = -20° across to l = 0, b = 30°.
The galaxy clusters themselves are not spread evenly on the sky: those within about 100 Mpc form a rough ellipsoid lying almost perpendicular to the Milky Way's disk. The Hydra-Centaurus concentration of galaxies in Figure 1.18, the Ursa Major group of Figures 5.6 and 5.8, and the Perseus cluster of Figure 6.26, all lie close to the Great Circle through Galactic longitude l = 140° and l = 320°, shown as a heavy line in Figure 7.1. The equator of the ellipsoid is the supergalactic plane; it is well-defined in the northern Galactic hemisphere (b > 0), but becomes rather scruffy in the south.
We often use supergalactic coordinates to describe the positions of
nearby galaxies. The pole or Z axis of the supergalactic plane
points to
l = 47.4°, b = 6.3°. We take the supergalactic
X direction
in the Galactic plane, pointing to l = 137.3°, b = 0,
while the
Y axis points close to the north Galactic pole at b = 90°,
so that Y  0 along the
Zone of Avoidance. The supergalactic
plane passes through the nearby Virgo cluster at right ascension
0 along the
Zone of Avoidance. The supergalactic
plane passes through the nearby Virgo cluster at right ascension
 = 12h, declination
= 12h, declination
 = 12°; the Perseus cluster, at
= 12°; the Perseus cluster, at
 = 3h,
= 3h,
 = 40°; and Fornax, at
= 40°; and Fornax, at
 = 4h,
= 4h,
 = -35°.
= -35°.
Figure 7.2 shows the positions of nearby
elliptical galaxies, within
about 20 Mpc. The distances to these objects have been
found by analyzing surface brightness fluctuations.
Even though the galaxies are too far away for us to distinguish individual
bright stars, the number N of stars falling within any arcsecond
square on the image has some random variation;
so the surface brightness of any square fluctuates about some
average value. The closer the galaxy, the fewer stars lie within each
square, and the stronger the fluctuations between neighboring
squares: when N is large, the fractional variation is proportional
to 1 /  N. So if we
measure the surface brightness
fluctuations in two galaxies where we know the relative luminosity of
the bright stars that emit most of the light, we can find their
relative distances.
N. So if we
measure the surface brightness
fluctuations in two galaxies where we know the relative luminosity of
the bright stars that emit most of the light, we can find their
relative distances.

|
Figure 7.2. Positions of nearby elliptical galaxies on the supergalactic X - Y plane; x shows the Milky Way. Shading indicates recession velocity Vrad - J. Tonry. |
This method only works for galaxies in which almost all the stars are at least 3 - 5 Gyr old. Then, nearly all the light comes from stars close to the tip of the red giant branch, which is sharply defined in luminosity. These stars have had time to make many orbits around the galaxy, so they are dispersed evenly through the system. The observations are usually made in the I band near 8000 Å, to minimize the contribution of the younger bluer stars. The technique fails in spiral galaxies, because their brightest stars are still on the main sequence. Since the average age of the stellar population changes across the face of the galaxy, so does the luminosity of those bright stars. Also, the luminous main-sequence stars are too short lived to move far from the stellar associations where they formed. Their clumpy distribution causes much stronger fluctuations in the galaxy's surface brightness than those from random variations in the number of older stars.
In Figure 7.2, we see that the Virgo cluster is roughly 16 Mpc away. It appears to consist of two separate pieces, which do not coincide exactly with the two velocity clumps of Section 6.5, around the galaxies M87 and M49. Here, galaxies in the northern part of the cluster, near M49, lie mainly in the nearer grouping, while those in the south near M86 are more distant; M87 lies between the two clumps. The Fornax cluster, in the south with Y < 0, is at about the same distance as Virgo. Both these clusters are seen as part of larger complexes of galaxies. Because galaxy groups contain relatively few ellipticals, they do not show up well in this figure. The Local Group is represented only by the elliptical and dwarf elliptical companions of M31, as the overlapping circles just to the right of the origin.
We can see in Figure 7.2 that galaxy clusters and groups are not very concentrated relative to their surroundings. Near the Sun, the average density of stars and gas in the Milky Way's disk corresponds to about 1 atom per cubic centimeter; this is over a million times greater than in the Universe as a whole. But in Section 6.5, we found that even in the center of a cluster like Virgo, the density of luminous galaxies is only a few thousand times more than average. Our Local Group contains only two sizable galaxies, the Milky Way and M31, plus a couple of dozen smaller ones, within a 1 Mpc radius; its density is only about ten times larger than the cosmic mean.
Problem 7.1: In Section 4.4 we saw that the motions of the Milky
Way and M31 indicate that the Local Group's mass exceeds 3
x 1012
M |
Problem 7.2: The time taken for a galaxy or cluster to grow to
density |
Figure 7.3 shows a `wedge diagram' with
positions and measured
redshifts of 24 418 galaxies in two slices across the sky: one in
the south, and one in the northern sky. If we ignore peculiar
velocities, Equation 1.21 tells us that the recession speed
Vr  cz
cz  H0 d, where H0 is the Hubble
constant;
the redshift is roughly proportional to the galaxy's
distance d from our position at the apex of each wedge. So this figure
gives us a somewhat distorted map of the region out to 600
h-1 Mpc.
H0 d, where H0 is the Hubble
constant;
the redshift is roughly proportional to the galaxy's
distance d from our position at the apex of each wedge. So this figure
gives us a somewhat distorted map of the region out to 600
h-1 Mpc.
The three-dimensional distribution of galaxies in
Figure 7.3 has
even more pronounced structure than Figure 7.1.
We see dense linear features, the walls and stringlike
filaments of galaxies; at their intersection are complexes of rich
clusters. Between the filaments we find large regions that are almost
empty of bright galaxies: these voids are typically
 50h-1
Mpc across.
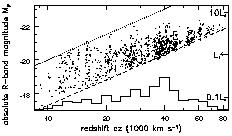
The galaxies appear to thin out beyond cz
50h-1
Mpc across.
The galaxies appear to thin out beyond cz
 40 000 km s-1,
because redshifts were measured only for objects that exceeded a fixed
apparent brightness. Figure 7.4
shows that at large distances, just the rarest and most luminous
systems have been included. When a solid angle
40 000 km s-1,
because redshifts were measured only for objects that exceeded a fixed
apparent brightness. Figure 7.4
shows that at large distances, just the rarest and most luminous
systems have been included. When a solid angle
 on the sky is
surveyed, the volume between distance d and d +
on the sky is
surveyed, the volume between distance d and d +
 d is
d is  V =
V =
 d2
d2
 d, which increases
rapidly with d. Accordingly, we see few galaxies nearby; most of
the measured objects lie near 40 000km s-1.
d, which increases
rapidly with d. Accordingly, we see few galaxies nearby; most of
the measured objects lie near 40 000km s-1.
|
Figure 7.4. Absolute R-band magnitude MR - 5 log10 h for 846 galaxies near 0h in the survey of Figure 7.3, plotted against redshift z. The arrow indicates L*, the luminosity of a typical bright galaxy; the histogram below shows numbers at each redshift. The survey included only galaxies brighter than apparent magnitude mR = 17.7 (dashed line) and fainter than mR = 15 (dotted line).} |
Problem 7.3: If the Local Group's motion of 600km s-1 relative to the cosmic background radiation represents a typical peculiar velocity, show that a galaxy would take ~ 50 h-1 Gyr to move from the center to the edge of a void 60 h-1 Mpc across. Whatever process removed material from the voids must have taken place very early, when the Universe was much more compact. |
Another way to probe the large-scale distribution is to
measure redshifts for galaxies within a narrow cone, but to
include fainter objects. Figure 7.5 shows the
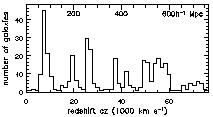
redshifts of 356 galaxies near the north Galactic pole.
The first peak, at redshift cz
 7000 or d = 70
h-1 Mpc,
corresponds to galaxies in the Great Wall, which
runs through the Coma cluster. Larger surveys show the Great Wall
stretching for 100h-1 Mpc, or a quarter of the way
around the sky.
Behind it, a succession of relatively empty voids alternates with more
distant walls.
7000 or d = 70
h-1 Mpc,
corresponds to galaxies in the Great Wall, which
runs through the Coma cluster. Larger surveys show the Great Wall
stretching for 100h-1 Mpc, or a quarter of the way
around the sky.
Behind it, a succession of relatively empty voids alternates with more
distant walls.
|
Figure 7.5. Distribution of redshifts for galaxies in a cone 4° x 49' across on the sky, near the north Galactic pole - see Willmer & Koo, ApJS 104, 199; 1996. |
In Figures 7.3 and 7.5, the walls appear to be several times denser than the void regions. However, the use of Equation 1.21 has exaggerated their narrowness and sharpness; they would appear less pronounced if we could plot the true distances of the galaxies. The Great Wall and similar structures are still collapsing on themselves. The extra mass concentrated in a wall or filament attracts nearby galaxies in front of the structure, pulling them toward it and away from us. So the radial velocities of those objects are increased above the cosmic expansion, and we overestimate their distances, placing them further from us and closer to the wall. Conversely, galaxies behind the wall are pulled in our direction, reducing their redshifts; these systems appear nearer to us and closer to the wall than they really are. In the Great Wall, the galaxy density is only a few times higher than the local average.
By contrast, dense clusters of galaxies appear elongated in the direction toward the observer. The cores of these clusters have completed their collapse. Galaxies there are packed tightly together in space, and orbit each other with random speeds as large as 1500km s-1, so their distances inferred from Equation 1.21 have random errors of ~ 15h-1 Mpc. In a wedge diagram, rich clusters appear as dense `fingers', pointing toward the observer; these are especially prominent in Figure 1.18.
In the left panel of Figure 7.6, we clearly see a cluster near 2h, at d = 400 h-1 Mpc. But in the right panel, the clustering in this region is much weaker - why? The galaxies of the right panel are red in color, and their spectra show little sign of recent star formation, while in the left we see blue galaxies, with spectral lines characteristic of young massive stars and the ionized gas around them. As we saw in Section 6.5, elliptical galaxies tend to lie in the cores of rich clusters, where spiral galaxies are rare. Accordingly, the clustering of the red galaxies differs from that of the bluer systems of the right panel. The region near 0h20m at d =200 h-1 Mpc is much richer in blue galaxies than red ones.
In fact, we should not talk simply of `the distribution of galaxies', but must be careful to specify which galaxies we are looking at. We never see all the galaxies in a given volume; our surveys are always biassed by the way we choose systems for observation. For example, if we select objects that are large enough on the sky that they appear fuzzy and hence distinctly non-stellar, we will omit the most compact galaxies. A survey that finds galaxies by the 21 cm radio emission of their neutral hydrogen gas will readily locate optically dim but gas-rich dwarf irregular galaxies, but will miss the luminous ellipticals, which usually lack HI gas. The Malmquist bias of Problem 2.9 is present in any sample selected by apparent magnitude. Even more insidious are the ways in which these biasses change with redshift and apparent brightness. Mapping even the luminous matter of the Universe is no easy task.