The primordial yields of light elements are determined by the competition
between the expansion rate of the Universe (the Hubble parameter H) and
the rates of the weak and nuclear reactions. It is the weak interaction,
interconverting neutrons and protons, that largely determines the amount
of he which may be synthesized, while detailed nuclear reaction rates
regulate the production (and destruction) of the other light elements.
In the standard model of cosmology the early expansion rate is fixed by
the total energy density 
,
where G is Newton's gravitational constant. In the standard
model of particle physics the early energy density is dominated
by the lightest, relativistic particles. For the epoch when
the Universe is a few tenths of a second old and older, and
the temperature is less than a few MeV,
where
In the standard model at T ~ 1 MeV, gSM = 43/4.
Account may be taken of additional degrees of freedom by comparing
their contribution to
If the early energy density deviates from that of the standard model, the
early expansion rate (or, equivalently, the age at a fixed temperature)
will change as well. The ``speed-up'' factor
As we'll see shortly, the he abundance is very sensitive to the early
expansion rate while the abundances of the other light nuclides depend
mainly on the nuclear reaction rates which scale with the nucleon (baryon)
density. Since the baryon density is always changing as the Universe
expands, it is convenient to distinguish between models with different
baryon densities using a dimensionless parameter which is either conserved
or, changes in a known and calculable fashion. From the very early Universe
till now the number of baryons in a comoving volume has been preserved and
the same is roughly true for photons since the end of BBN. Therefore, the
ratio of number densities of baryons (nB) and photons
(n
The universal density of photons at present (throughout this article the
present epoch is indicated by the subscript `0') is dominated by those in
the CBR (for T0 = 2.73 K, n
It should be noted that prior to electron-positron annihilation there
were fewer photons in every comoving volume (by a factor very close to
4/11); this is automatically accounted for in all numerical BBN codes.
It is simply a matter of consensus and convenience that the baryon
abundance is quoted in terms of its present value.
In SBBN (i.e., N
Figure 1. The predicted primordial
abundances as a function of
,
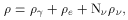
e, and
are the energy densities
in photons, electrons and positrons, and massless neutrinos and antineutrinos
(one species), respectively;
N is the number of
massless (or, very light:
m << 1 MeV)
neutrino species which, in standard BBN, is
exactly 3. In considering variations on the theme of the standard model,
it is useful to allow
N to differ from 3
to account for the presence
of ``new'' particles and/or any suppression of the standard particles
(e.g., if the 
neutrino
should have a large mass). Since the energy density
in relativistic particles scales as the fourth power of the temperature,
the early expansion rate scales as the square of the temperature with a
coefficient that depends on the number of different relativistic
species. The more such species, the faster the Universe expands, the
earlier (higher temperature) will the weak and nuclear reactions drop
out of equilibrium. It is useful to write the total energy density in
terms of the photon energy density and g, the equivalent number
of relativistic degrees
of freedom (i.e., helicity states, modulo the different
contributions to the energy density from fermions and bosons),
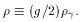
to that of one additional light neutrino species.
H / HSM may
be related to 
N by,
)
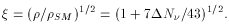
provides just such a measure of the universal baryon abundance.
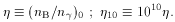
0 = 412 cm-3) so that the
baryon density parameter
B
(B /
c)0, the ratio of the present baryon
density (B) to the present critical density
(c), may
be related to 
and
the present value of the Hubble parameter H0
100 h km s-1
Mpc-1,
)
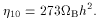
the abundances of the light nuclides
synthesized primordially depend on only one ``free'' parameter,
.
SBBN is thus ``overconstrained'' since one value (or, a narrow range
of values set by the observational and theoretical reaction rate
uncertainties) of
must account consistently for the primordial
abundances of D, 3He, 4He and 7Li. At
the same time this value/range of
must be consistent with current estimates of (or, bounds to)
the present baryon density. For these reasons BBN is one of the key
pillars supporting the edifice of the standard model of cosmology and,
it is the only one which offers a glimpse of the earliest evolution of
the Universe. In the following we'll first identify the key landmarks
in the first 20 minutes in the evolution of the Universe in order to
identify the physical processes responsible for determining the primordial
abundances of the light nuclides. Then, after presenting the SBBN
predictions (as a function of
; see
Fig. 1) we will review the
current status of the observational data, as well as the steps necessary
in order to go from ``here and now'' to ``there and then'' when using
the data to infer the true primordial abundances. Then we will be
in a position to assess the consistency of the standard model.
.
YP is the 4He mass fraction while
y2P, y3P,
y7P are the number density ratios to hydrogen of D,
3He, and 4He respectively.