


2.1. Weak Equilibrium and the he Abundance
Consider now those early epochs when the Universe was only a few tenths
of a second old and the radiation filling it was at a temperature (thermal
energy) of a few MeV. According to the standard model, at those early
times the Universe was a hot, dense ``soup'' of relativistic particles
(photons, e± pairs, 3 ``flavors'' (e, µ,
 ) of
neutrino-antineutrino pairs) along with a trace amount (at the level
of a few parts in 1010) of neutrons and protons. At such high
temperatures and densities both the weak and nuclear reaction rates
are sufficiently rapid (compared to the early Universe expansion rate)
that all particles have come to equilibrium. A key consequence of
equilibrium is that the earlier history of the evolution of the Universe
is irrelevant for an understanding of BBN. When the temperature drops
below a few MeV the weakly interacting neutrinos effectively decouple
from the photons and e± pairs, but they still play an
important role in regulating the neutron-to-proton ratio.
) of
neutrino-antineutrino pairs) along with a trace amount (at the level
of a few parts in 1010) of neutrons and protons. At such high
temperatures and densities both the weak and nuclear reaction rates
are sufficiently rapid (compared to the early Universe expansion rate)
that all particles have come to equilibrium. A key consequence of
equilibrium is that the earlier history of the evolution of the Universe
is irrelevant for an understanding of BBN. When the temperature drops
below a few MeV the weakly interacting neutrinos effectively decouple
from the photons and e± pairs, but they still play an
important role in regulating the neutron-to-proton ratio.
At high temperatures, neutrons and protons are continuously interconverting
via the weak interactions: n + e+ <-> p
+  e, n +
e, n +
 e <-> p +
e-, and n <-> p + e- +
e <-> p +
e-, and n <-> p + e- +
 e. When the
interconversion rate is faster than the expansion
rate, the neutron-to-proton ratio tracks its equilibrium value, decreasing
exponentially with temperature (n / p = e-
e. When the
interconversion rate is faster than the expansion
rate, the neutron-to-proton ratio tracks its equilibrium value, decreasing
exponentially with temperature (n / p = e- m / T, where
m / T, where
 m = 1.29 MeV is the
neutron-proton mass difference). A comparison of the weak
rates with the universal expansion rate reveals that equilibrium may be
maintained until the temperature drops below ~ 0.8 MeV. When the
interconversion rate becomes less than the expansion rate, the n/p ratio
effectively ``freezes-out'' (at a value of
m = 1.29 MeV is the
neutron-proton mass difference). A comparison of the weak
rates with the universal expansion rate reveals that equilibrium may be
maintained until the temperature drops below ~ 0.8 MeV. When the
interconversion rate becomes less than the expansion rate, the n/p ratio
effectively ``freezes-out'' (at a value of
 1/6), thereafter
decreasing slowly, mainly due to free neutron decay.
1/6), thereafter
decreasing slowly, mainly due to free neutron decay.
Although n/p freeze-out occurs at a temperature below the deuterium
binding energy, EB = 2.2 MeV, the first link in the
nucleosynthetic chain, p + n -> D +
 , is ineffective
in jump-starting BBN since the photodestruction rate of deuterium
(
, is ineffective
in jump-starting BBN since the photodestruction rate of deuterium
( n
n e-EB / T) is much larger than the deuterium
production rate (
e-EB / T) is much larger than the deuterium
production rate ( nB) due to the very large universal photon-to-baryon
ratio (
nB) due to the very large universal photon-to-baryon
ratio ( 109).
Thus, the Universe must ``wait'' until there are so few sufficiently
energetic photons that deuterium becomes effectively stable against
photodissociation. This occurs for temperatures
109).
Thus, the Universe must ``wait'' until there are so few sufficiently
energetic photons that deuterium becomes effectively stable against
photodissociation. This occurs for temperatures
 80 keV, at which
time neutrons are rapidly incorporated into he with an efficiency of
99.99%. This efficiency is driven by the tight binding of the 4He
nucleus, along with the roadblock to further nucleosynthesis imposed
by the absence of a stable nucleus at mass-5. By this time (T
80 keV, at which
time neutrons are rapidly incorporated into he with an efficiency of
99.99%. This efficiency is driven by the tight binding of the 4He
nucleus, along with the roadblock to further nucleosynthesis imposed
by the absence of a stable nucleus at mass-5. By this time (T
 80 keV), the n/p
ratio has dropped to ~ 1/7, and simple counting
(2 neutrons in every 4He nucleus) yields an estimated
primordial 4He mass fraction
80 keV), the n/p
ratio has dropped to ~ 1/7, and simple counting
(2 neutrons in every 4He nucleus) yields an estimated
primordial 4He mass fraction
As a result of its large binding energy and the gap at mass-5, the
primordial abundance of 4He is relatively insensitive to the
nuclear reaction rates and, therefore, to the baryon abundance
(
Figure 2. The predicted 4He
abundance (solid curve) and the 2
The 4He abundance is, however, sensitive to the competition between
the universal expansion rate (H) and the weak interaction rate
(interconverting neutrons and protons). If the early Universe should
expand faster than predicted for the standard model, the weak interactions
will drop out of equilibrium earlier, at a higher temperature, when the
n/p ratio is higher. In this case, more neutrons will be available to
be incorporated into 4He and YP will increase.
Numerical calculations show that for a modest speed-up
(
It should be noted that the uncertainty in the BBN-predicted mass
fraction of 4He is very small and almost entirely dominated by the
(small) uncertainty in the n - p interconversion rates. These rates
may be ``normalized'' through the neutron lifetime,
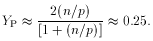
 ). As
may be seen in Figure 1, while
). As
may be seen in Figure 1, while
 varies by orders of magnitude, the predicted 4He mass
fraction, YP, changes by factors of only a few.
Indeed, for 1
varies by orders of magnitude, the predicted 4He mass
fraction, YP, changes by factors of only a few.
Indeed, for 1 
 10
10
 10, 0.22
10, 0.22
 YP
YP
 0.25.
As may be seen in Figures 1 and
2, there is a very slight increase in YP
with
0.25.
As may be seen in Figures 1 and
2, there is a very slight increase in YP
with  .
This is mainly due to BBN beginning earlier, when there are
more neutrons available to form 4He, if the baryon-to-photon
ratio is higher. The increase in YP with
.
This is mainly due to BBN beginning earlier, when there are
more neutrons available to form 4He, if the baryon-to-photon
ratio is higher. The increase in YP with
 is logarithmic; over
most of the interesting range in
is logarithmic; over
most of the interesting range in
 ,
,
 YP
YP
 0.01
0.01

 /
/  .
.
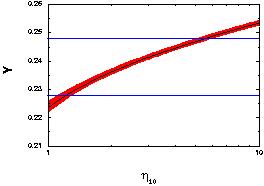
 theoretical uncertainty
[3]. The
horizontal lines show the
range indicated by the observational data.
theoretical uncertainty
[3]. The
horizontal lines show the
range indicated by the observational data.
 N
N
 1),
1),
 YP
YP
 0.013
0.013
 N
N . Hence, constraints on YP
(and
. Hence, constraints on YP
(and  )
lead directly to bounds on
)
lead directly to bounds on
 N
N and, on particle physics
beyond the standard model
[1].
and, on particle physics
beyond the standard model
[1].
 n, whose
current standard value is 887 ± 2 s (actually, 886.7 ± 1.9 s).
To very good accuracy, a 1 s uncertainty in
n, whose
current standard value is 887 ± 2 s (actually, 886.7 ± 1.9 s).
To very good accuracy, a 1 s uncertainty in
 n
corresponds to an uncertainty in YP of order 2 x
10-4. At this tiny
level of uncertainty it is important to include finite mass, zero- and
finite-temperature radiative corrections, and Coulomb corrections to
the weak rates. However, within the last few years it emerged that
the largest error in the BBN-prediction of YP was due to a too large
time-step in the numerical code. With this now under control, it is
estimated that the residual theoretical uncertainty (in addition to
that from the uncertainty in
n
corresponds to an uncertainty in YP of order 2 x
10-4. At this tiny
level of uncertainty it is important to include finite mass, zero- and
finite-temperature radiative corrections, and Coulomb corrections to
the weak rates. However, within the last few years it emerged that
the largest error in the BBN-prediction of YP was due to a too large
time-step in the numerical code. With this now under control, it is
estimated that the residual theoretical uncertainty (in addition to
that from the uncertainty in
 n) is of the order of 2 parts
in 104. Indeed, a comparison of two major, independent BBN codes
reveals agreement in the predicted values of YP to 0.0001
± 0.0001 over the entire range 1
n) is of the order of 2 parts
in 104. Indeed, a comparison of two major, independent BBN codes
reveals agreement in the predicted values of YP to 0.0001
± 0.0001 over the entire range 1

 10
10
 10. In
Figure 2 is
shown the BBN-predicted he mass fraction, YP, as a function of
10. In
Figure 2 is
shown the BBN-predicted he mass fraction, YP, as a function of
 ; the thickness of
the band is the ±2
; the thickness of
the band is the ±2 theoretical
uncertainty. For
theoretical
uncertainty. For
 10
10
 2 the
1
2 the
1 theoretical uncertainty in
Yp is
theoretical uncertainty in
Yp is  6 x
10-4. As we will soon see, the current
observational uncertainties in YP are much larger (see, also,
Fig. 2).
6 x
10-4. As we will soon see, the current
observational uncertainties in YP are much larger (see, also,
Fig. 2).