1. QUALITATIVE CLASSIFICATIONS

The revised 3-dimensional Hubble classification system (de Vaucouleurs 1959, 1963, 1974; Sandage 1961, 1975) is still basic. Other systems (Yerkes: Morgan 1958, 1959; DDO: van den Bergh 1960; RDDO: van den Bergh 1976; Byurakan: Tovmassian 1964) provide important additional information. Revised T types are now available for over 4000 galaxies, but for less than 1000 in other systems (Table 1). Even though all such systems are still entirely subjective, independent classifications by trained observers agree fairly closely (Corwin 1968, Nilson 1973, Buta 1977). In general the reliability of a classification depends on telescope aperture, plate scale and image area as well as inclination. In good cases of nearly face-on objects classified on original plates with N > 10⁴ pixels in image area the m.e. of T types can be as small as 5 percent of the range; classifications on small-scale, high contrast prints such as the POSS copies have much lower weight (at the limit all galaxies appear "elliptical").

Because most systems are highly correlated (de Vaucouleurs 1963) and the revised Hubble system gives the best "resolution" (range / ), the closest correlation with physical parameters as well as the most extensive overlap with other systems, it is expedient to consider T as the basic qualitative parameter and to correlate it with other qualitative systems and with quantitative parameters. The following report updates or supersedes results reviewed at the Canberra (IAU 58) 1973 symposium (de Vaucouleurs 1974); as far as possible statistics are based on the Second Reference Catalogue of Bright Galaxies (RC2) (de Vaucouleurs et al. 1976).

Table 1. Principal empirical classification systems

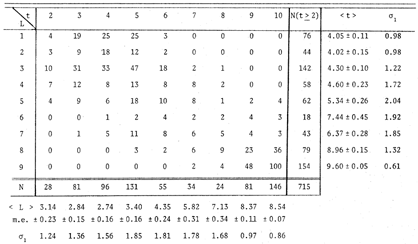
System	Type	Range of Scale 1	Number of Galaxies 1	<  >	< > / Range	Rem.
Hubble revised	Morphological T	-5 to +10   (E to Im)	3811	0.9	0.06	(1)
DDO	Luminosity L	1 to 9 (I to V)	~711	~ 1.	0.12	(2)
Yerkes	Form-color Y(1) Y(2)	1 to 7 (A to K)	608 645	0.6	0.10	(3)
Byurakan	Nuclear type N(1)	1 to 5	516	~ 1.	~ 0.2	(4)
BGC	Nuclear class N(2)	1 to 5	1239	~ 1.	~ 0.2	(5)
1 In Second Reference Catalogue of Bright Galaxies (RC2).
(1) de Vaucouleurs (1963) and RC2; additional T types in Nilson (1973); w = 0.2 to 5.0 ( = 3 to 0.5), = 2.6, < > = 0.9; additional stages T = -6 (compact E) and +11 (compact Im) (de Vaucouleurs 1974) are rare.
(2) van den Bergh (1960, 1976), Sandage and Tammann (1974), Fisher and Tully (1975); additional L classes for 209 galaxies in Rubin et al. (1976).
(3) Yerkes list 1 (Morgan 1958); Yerkes list 2 (Morgan 1959).
(4) Tovmassian et al. (1964 - 73) nuclear concentration scale; see references in RC2.
(5) From BGC description of nuclear brightness; see RC2.

1.1 Morphological Type and Luminosity Class: Luminosity Index

The DDO luminosity class L is highly correlated with type T (Fig. 1); this is because the DDO system used only the original Sa, Sb, Sc Hubble stages and essentially bridges the gap to magellanic irregulars Im by means of luminosity classes IV, V attached to Sc; conversely, the revised Hubble system introduces late-spiral stages Sd, Sm across this gap, but has no luminosity classes. Each system provides some information not given by the other; because of this and the fact that each is subject to classification errors of ~ 12 percent (over the restricted range 2 T 10, i.e., Sab to Im, over which the L classification is valid) it is convenient to combine them into a composite luminosity index = (T + L) / 10 which is more closely correlated with absolute magnitude than either T or L alone (de Vaucouleurs 1976).

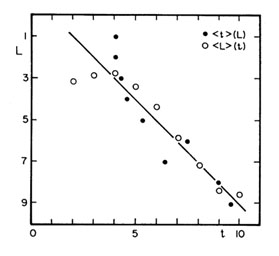
Figure 1. Correlation between morphological type t arid DDO luminosity class L. t is revised Hubble stage index from -5 (E) to +10 (Im), L = 1 to 9 (Lc = I toV).

Excluding a few early types (L, Sa) which were misclassified as later-type spirals in the DDO system because of inadequate resolution (POSS paper prints!), the mean relation is simply T = L + 1.0, with a s.d. (L - T) = 1.4, consistent with mean errors (L) (T) 1.0 step for each system. The total range of is from 0.3 (Sab I) to 1.9 (Im V) with a resolution = range / = 1.6 / 0.14 = 11. Extensive tests of the correlation between and the corrected absolute magnitude M°_T (in the B°_T system of RC2) lead (without arbitrary extra-polation) to the adopted regression line

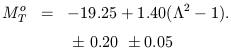
(1)

Table 2. Numbers of galaxies of each t type and l class

The constant is derived from 9 nearby galaxies (0.5 1.5) having distances from primary and secondary indicators (de Vaucouleurs 1977b); the coefficient of ² is derived from the apparent magnitudes of 22 galaxies in the Virgo cluster and from provisional absolute magnitudes of 351 galaxies calculated from their redshifts (assuming linearity) (Fig. 2). ⁽¹⁾

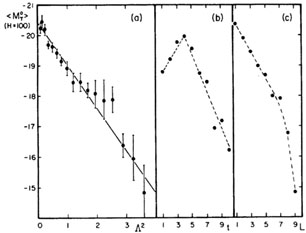
Figure 2. Correlation between mean corrected total B absolute magnitudes < M°T > (from redshifts for H = 100) and (a) luminosity index , (b) morphological type t, (c) luminosity class L.

If B°_T(1) = B°_T - 1.4(² - 1), the geometric distance modulus of any spiral for which B°_T, T and L are known is given by µ₀ = 19.25 + B±_T(1) with an estimated mean error (µ₀) 0.5 mag if < 1.5. The error increases for 1.5, i.e., for late-type dwarfs which have an intrinsically greater dispersion of absolute magnitudes (de Vaucouleurs 1958a). In other words the T and L classification criteria give poor luminosity discrimination among late-type systems (T > 6, L > 5); in particular, both nearby low-luminosity and distant high-luminosity systems are mixed among the DDO "dwarfs" (Fisher and Tully 1975). Magellanic irregulars span a very large range of luminosities from extreme dwarfs such as DDO 155 = GR 8 = A 1256 + 14 with M°_T -11 (Hodge 1974, de Vaucouleurs 1977b) up to "clumpy" giant systems such as Mark 325 at M°_T -20 (Casini and Heidmann 1976), but the average still agrees with equation (1).

1.2 Morphological Type and Yerkes Color Class

The correlation between the two Yerkes lists Y1, Y2 and the revised Hubble typo T has been analyzed previously (de Vaucouleurs 1963) (Fig. 3). The main interest of the Y types is in its providing additional information on the bulge/disk ratio and in its (weak) correlation with color residuals at constant type T (Section 2.2).

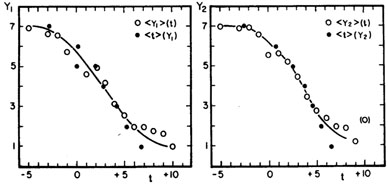
Figure 3. Correlations between morphological type t and the two lists Y1, Y2 of Yerkes types (color classes).

1.3 Morphological Type and Byurakan Nuclear Type

Byurakan nuclear types N' were examined for systematic errors dependent on apparent diameter and inclination. No significant effect of apparent diameter was found, but an effect of axis ratio R = a/b is present for types t > -2, that is

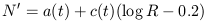
where c(t) -1.5 ± 0.3 for t > -2 (0 for t -2). This is clearly an effect of internal obscuration of the nucleus in dusty galaxies. The inclination-corrected type N'_c = N + 1.5(log R - 0.2) shows a loose, but significant correlation with morphological type T in the expected sense as shown in Fig. 4; that is, late types (t 5) have weaker nuclei than early types, but the scatter is large. Occasional confusion between nuclei and bright HII regions has been noted (e.g. in NGC 55), especially among late types.

Figure 4. Correlations between morphological type t and corrected nuclear types from Byurakan (N'c) and BGC (N''c). Means for magellanic irregulars (t = 9, 10) are after rejection of some misclassifications.

1.4 Morphological Type and BGC Nuclear Class

The BGC nuclear classes N'' coded as in RC2 (Table 1) were likewise investigated for resolution and inclination effects using the weight (log W) and axis ratio (log R) as parameters. As for the Byurakan data, an effect of inclination (obscuration) was indicated with c(t) = 0 for t -2, c(t) = -1.5 ± 0.2 for t > -2. The effect of resolution measured by the weight log W of the morphological classification (function of image size and plate scale as explained in RC2) was expressed by

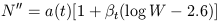
where _t = 0 for t -4 (E), 0.058 ± 0.014 for -3 t 0 (L), 0.115 ± 0.013 for 1 t 4 (Sa-Sbc) and 0.049 ± 0.023 for 5 t 10 (Sc-Im). The corrected class N''_c is correlated with morphological type in the same sense as the Byurakan types (Fig. 4).

1.5 Morphological Type and Revised DDO System

There is a loose correlation between the revised DDO system (van den Bergh 1976) and the revised Hubble types T (Table 3). RDDO has more steps among lenticulars and early spirals (making up the S0 and A classes of RDDO) and fewer among the late-type spirals and irregulars (comprising the Sc, Sc/Irr, and Irr of RDDO). Essentially, the late L and early S stages (-2 t 2) have been depleted to form the "anemic spiral" A class. The rationale offered for this reshuffling is that it improves the correlation with color indices and bulge/disk ratio. I have been unable to substantiate this claim from a study of available quantitative data for the small set of 126 examples of RDDO types in the Hubble Atlas. In particular the claim that anemic spirals (A) are redder than normal spirals (5) of the same Hubble stage is not verified; in the best documented case the mean color of RDDO Ab objects of types t = 1 to 3 (Sa - Sb) is <(B - V)°_T> = 0.73 compared with 0.74 for RDDO Sb in the same t range (see Section 2.2c).

⁽¹⁾ The constant term implies < H₀ > 90 (1 ± 0.1) km s^-1 Mpc^-1 for the local all-sky average of the Hubble ratio for 300 spirals having distance moduli µ₀ < 33, in agreement with H₀ = 86 (1 ± 0.1) independently derived from globular clusters in ellipticals of 3 galaxy clusters (Hanes 1977, de Vaucouleurs 1977a). Back.