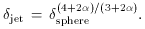4.4 Brightness Temperature Calculations and SSC Models
The smooth nonthermal radio-through-infrared continuum
emission in radio-loud AGN is probably synchrotron
radiation, i.e., emission from relativistic electrons moving
in a magnetic field. Some of the synchrotron photons will be
inverse Compton scattered to higher energies by the
relativistic electrons, which is known as the synchrotron
self-Compton (SSC) process. For some radio-loud AGN the
synchrotron radiation density inferred from the observed
radio power and angular size predicts SSC X-rays well in
excess of the observed X-ray flux
(Marscher et al. 1979;
Ghisellini et al. 1993),
which is called the ``Compton catastrophe''
(Hoyle et al. 1966).
A related (but not equivalent) statement
is that extremely rapid radio variability in some blazars
(Quirrenbach et
al. 1992)
implies brightness temperatures,
TB = I c2 /
(2k
c2 /
(2k 2), where
k is Boltzman's
constant, larger than the 1012 K limit
(Kellermann and
Pauliny-Toth 1969; see also
Singal and
Gopal-Krishna 1985
and Readhead 1994,
who suggest a limit TB
2), where
k is Boltzman's
constant, larger than the 1012 K limit
(Kellermann and
Pauliny-Toth 1969; see also
Singal and
Gopal-Krishna 1985
and Readhead 1994,
who suggest a limit TB  1011 K
appropriate to the equipartition of magnetic field and relativistic
electron energy densities).
1011 K
appropriate to the equipartition of magnetic field and relativistic
electron energy densities).
It follows that the true synchrotron photon density must be
lower than observers infer by assuming isotropy. The strong
anisotropy and shortened time scales caused by relativistic
beaming can account naturally for the Compton catastrophe
(or non-catastrophe, as it happens). A lower limit to
the Doppler factor,  , which
characterizes these effects
(Appendix B)
can be estimated from the ratio of predicted to
observed SSC flux
(Jones et al. 1974;
Marscher et al. 1979).
In the case of a spherical emission region of observed angular
diameter
, which
characterizes these effects
(Appendix B)
can be estimated from the ratio of predicted to
observed SSC flux
(Jones et al. 1974;
Marscher et al. 1979).
In the case of a spherical emission region of observed angular
diameter  d,
moving with Doppler
factor
d,
moving with Doppler
factor  sphere, the
limit is
(Ghisellini et
al. 1993):
sphere, the
limit is
(Ghisellini et
al. 1993):
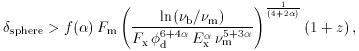 (2)
(2)
where  d is in
milliarcseconds,
d is in
milliarcseconds,
 m is the observed
self-absorption
frequency of the synchrotron spectrum in GHz, Fm is
the observed radio flux at
m is the observed
self-absorption
frequency of the synchrotron spectrum in GHz, Fm is
the observed radio flux at  m
in Jy, Ex and Fx are the observed
X-ray energy and
flux in keV and Jy respectively, and
m
in Jy, Ex and Fx are the observed
X-ray energy and
flux in keV and Jy respectively, and  b is the observed synchrotron
high frequency cut-off. The function f(
b is the observed synchrotron
high frequency cut-off. The function f( ), where
), where  is
the spectral index of the optically thin synchrotron
emission, depends only weakly on the various assumptions
used by different authors (see discussion in
Urry 1984) and
has the approximate value f(
is
the spectral index of the optically thin synchrotron
emission, depends only weakly on the various assumptions
used by different authors (see discussion in
Urry 1984) and
has the approximate value f( )
)  0.08
0.08  +
0.14 (Ghisellini 1987). If the radio source is a continuous
jet, which is perhaps more realistic
(Appendix B, case
p = 2 +
+
0.14 (Ghisellini 1987). If the radio source is a continuous
jet, which is perhaps more realistic
(Appendix B, case
p = 2 +  ), then
(Ghisellini et
al. 1993):
), then
(Ghisellini et
al. 1993):
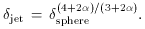 (3)
(3)
For a continuous jet compared to a single blob, therefore, the same
observed quantities
imply a higher Doppler beaming factor (for  > 1).
> 1).
The limit in Eq. (2) has been calculated for many
radio-loud AGN
(Marscher et al. 1979;
Madejski and Schwartz
1983;
Madau et al. 1987),
with the result that  has
lower limits both larger and smaller than unity, depending
on the AGN. One complication is that the angular size
(
has
lower limits both larger and smaller than unity, depending
on the AGN. One complication is that the angular size
( d) is a function
of observation frequency and so
is to some extent arbitrary. A self-consistent approach is
to use, in Eq. (2), the observing frequency as
d) is a function
of observation frequency and so
is to some extent arbitrary. A self-consistent approach is
to use, in Eq. (2), the observing frequency as
 m and the flux and
angular size (preferably measured
with VLBI) at that frequency as Fm and
m and the flux and
angular size (preferably measured
with VLBI) at that frequency as Fm and  d, respectively.
d, respectively.
For ~ 100 radio sources for which the VLBI size of the
radio-emitting core is published, Eq. (2) gives
 > 1 for a large fraction of BL
Lacs and essentially all FSRQ
(Ghisellini et
al. 1993).
That is, blazars for
which appropriate data exist do appear to have
relativistically beamed emission. Similarly, using
variability time scales to infer Doppler factors from the
condition TB, max < 1012 K gives
> 1 for a large fraction of BL
Lacs and essentially all FSRQ
(Ghisellini et
al. 1993).
That is, blazars for
which appropriate data exist do appear to have
relativistically beamed emission. Similarly, using
variability time scales to infer Doppler factors from the
condition TB, max < 1012 K gives  > 1 for a
number of blazars (Teräsranta and Valtaoja 1994). The
latter values for BL Lacs are somewhat low
compared to the SSC calculation, but if the equipartition
brightness temperature is more appropriate
(Singal and
Gopal-Krishna 1985;
Readhead 1994),
the derived Doppler factors increase by a factor of 2-3,
since
> 1 for a
number of blazars (Teräsranta and Valtaoja 1994). The
latter values for BL Lacs are somewhat low
compared to the SSC calculation, but if the equipartition
brightness temperature is more appropriate
(Singal and
Gopal-Krishna 1985;
Readhead 1994),
the derived Doppler factors increase by a factor of 2-3,
since  = [TB,
obs / TB, max]1/3.
= [TB,
obs / TB, max]1/3.



 c2 /
(2k
c2 /
(2k 2), where
k is Boltzman's
constant, larger than the 1012 K limit
(Kellermann and
Pauliny-Toth 1969; see also
Singal and
Gopal-Krishna 1985
and Readhead 1994,
who suggest a limit TB
2), where
k is Boltzman's
constant, larger than the 1012 K limit
(Kellermann and
Pauliny-Toth 1969; see also
Singal and
Gopal-Krishna 1985
and Readhead 1994,
who suggest a limit TB  1011 K
appropriate to the equipartition of magnetic field and relativistic
electron energy densities).
1011 K
appropriate to the equipartition of magnetic field and relativistic
electron energy densities).



 , which
characterizes these effects
(
, which
characterizes these effects
( d,
moving with Doppler
factor
d,
moving with Doppler
factor 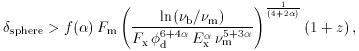
 ), where
), where  0.08
0.08