(B6)
Equations (B4), (B5), and (B6)
assume that the emission comes from a moving source, so they
apply to the case of discrete, essentially point-like, components. For a
smooth, continuous jet, the observed emitting volume is decreased by one power
of the Doppler factor because of Lorentz contraction, so that the exponents
in Eqs. (B4), (B5), and (B6)
become 2 +  , 3, and 4,
respectively
(Begelman et al. 1984;
Cawthorne 1991;
Ghisellini et
al. 1993).
, 3, and 4,
respectively
(Begelman et al. 1984;
Cawthorne 1991;
Ghisellini et
al. 1993).
Relaxing the assumption of isotropic emission in the rest frame can also
change the relationship between intrinsic and observed flux. If the source is
an optically thin jet with magnetic field parallel to its axis, then in the
rest frame F' '(
'( ' )
' )
 (sin
(sin
 ' )1+
' )1+ . Since
sin
. Since
sin  ' =
' =  sin
sin
 , Eq. (B4)
becomes F
, Eq. (B4)
becomes F (
( ) =
) =
 (3+2
(3+2 ) (sin
) (sin
 )1+
)1+ F'
F' '(
'( )
(Cawthorne 1991;
Begelman 1993).
)
(Cawthorne 1991;
Begelman 1993).
So far we have assumed power-law emission in the rest-frame. Strictly
speaking, for synchrotron emission this would mean the jet is either
completely optically thin (F

 -
- ,
, 
 0.5)
or completely optically thick (F
0.5)
or completely optically thick (F

 5/2). Real jets are
probably inhomogeneous and have flat spectra caused by the superposition of
individual synchrotron components with different self-absorption frequencies.
Relativistic beaming distorts these components differentially because of the
dependence of optical depth and F
5/2). Real jets are
probably inhomogeneous and have flat spectra caused by the superposition of
individual synchrotron components with different self-absorption frequencies.
Relativistic beaming distorts these components differentially because of the
dependence of optical depth and F on
on  , so the overall spectral
shape should change. For a standard conical jet with tangled magnetic field,
the integrated flux transforms approximately as
, so the overall spectral
shape should change. For a standard conical jet with tangled magnetic field,
the integrated flux transforms approximately as  2+
2+ , where
, where
 refers to the observed
integrated spectrum rather than the spectral
index of the local emission
(Cawthorne 1991).
refers to the observed
integrated spectrum rather than the spectral
index of the local emission
(Cawthorne 1991).
Additional complications in the evaluation of the amplification factor include
the lifetimes of the emitting components, the radial dependence of the their
emissivities, and the presence of shocks
(Lind and Blandford
1985).
In the following we will hide all these possibilities in a single parameter,
p, by
assuming that the observed luminosity, Lj, of a
relativistic jet is related
to its intrinsic luminosity, 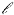 j, via
j, via
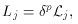 (B7)
(B7)
with p = 3 +  for a
moving, isotropic source and p =
2 +
for a
moving, isotropic source and p =
2 +  for a
continuous jet (other values are certainly possible).
for a
continuous jet (other values are certainly possible).
The recent detection of superluminal motion within our own Galaxy
(Mirabel and
Rodríguez 1994)
permits for the first time a direct estimate of p. Since
proper motions are measured for both the approaching and receding components,
 cos
cos  is
uniquely determined to be 0.323 ± 0.016 (where
is
uniquely determined to be 0.323 ± 0.016 (where
 refers to the
pattern speed;
Mirabel and
Rodríguez 1994).
Using the observed jet/counter-jet ratio, Fj /
Fcj = 8 ± 1, and assuming the
bulk speed in Eq. (A8) is equal to the pattern speed, we find
p = 3.10 ± 0.25.
One might expect p = 3 +
refers to the
pattern speed;
Mirabel and
Rodríguez 1994).
Using the observed jet/counter-jet ratio, Fj /
Fcj = 8 ± 1, and assuming the
bulk speed in Eq. (A8) is equal to the pattern speed, we find
p = 3.10 ± 0.25.
One might expect p = 3 +  because the components are discrete blobs,
whereas our estimate implies p
because the components are discrete blobs,
whereas our estimate implies p  2 +
2 +  since the measured spectral
index is
since the measured spectral
index is  = 0.8. Alternatively,
p ~ 3.8 is allowed if the bulk speed
is actually lower than the pattern speed, with a ratio
= 0.8. Alternatively,
p ~ 3.8 is allowed if the bulk speed
is actually lower than the pattern speed, with a ratio  bulk /
bulk /  pattern ~ 0.8
(cf.
Bodo and Ghisellini
1995).
pattern ~ 0.8
(cf.
Bodo and Ghisellini
1995).
Regardless of the precise value of p, relativistic beaming has a
very strong effect on the observed luminosity. A relativistic jet has



 2
2 for
for 
 arcsin
arcsin  -1
(Appendix A), meaning
a modest bulk Lorentz factor of
-1
(Appendix A), meaning
a modest bulk Lorentz factor of  = 10 amplifies the intrinsic power by
2-5 orders of magnitude (depending on p). The Doppler boosted
radiation is
strongly collimated and sharply peaked: at
= 10 amplifies the intrinsic power by
2-5 orders of magnitude (depending on p). The Doppler boosted
radiation is
strongly collimated and sharply peaked: at  ~ 1/
~ 1/ ~
6°l, the observed jet power is already ~ 4-16 times fainter than
at
~
6°l, the observed jet power is already ~ 4-16 times fainter than
at  = 0° (for p =
2-4). At 90°, the reduction is
huge, a factor of ~ 104 - 108. Although this is a
very large ratio, it
is actually much smaller than the inferred extinction at optical wavelengths
caused by an obscuring torus, which can be up to a factor of 1020
(Djorgovski et
al. 1991).
= 0° (for p =
2-4). At 90°, the reduction is
huge, a factor of ~ 104 - 108. Although this is a
very large ratio, it
is actually much smaller than the inferred extinction at optical wavelengths
caused by an obscuring torus, which can be up to a factor of 1020
(Djorgovski et
al. 1991).



 (Appendix A), relates intrinsic and
observed flux for a source moving at relativistic speed v
=
(Appendix A), relates intrinsic and
observed flux for a source moving at relativistic speed v
=  c.
For an approaching source, time intervals measured in the observer frame are
shorter than in the rest frame (even allowing for time dilation) because the
emitter ``catches up'' to its own photons:
c.
For an approaching source, time intervals measured in the observer frame are
shorter than in the rest frame (even allowing for time dilation) because the
emitter ``catches up'' to its own photons:



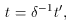
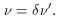
 /
/
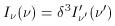
 =
=  (
( , Eq. (B3) becomes
, Eq. (B3) becomes
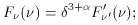
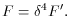
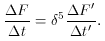
 ' )
' )
 0.5)
or completely optically thick (F
0.5)
or completely optically thick (F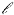 j, via
j, via
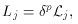
 2 +
2 + 
