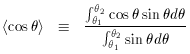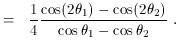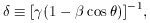
where  is its bulk
velocity in units of the speed of light,
is its bulk
velocity in units of the speed of light,
 = (1 -
= (1 -  2)-1/2 is the corresponding Lorentz
factor, and
2)-1/2 is the corresponding Lorentz
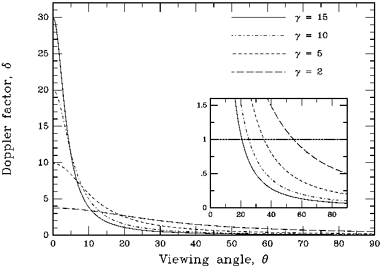
factor, and  is the angle between the velocity vector and the line of sight. The Doppler
factor has a strong dependence on the viewing angle (as shown in
Fig. 20), which gets stronger for larger
Lorentz factors. For
0°
is the angle between the velocity vector and the line of sight. The Doppler
factor has a strong dependence on the viewing angle (as shown in
Fig. 20), which gets stronger for larger
Lorentz factors. For
0° 

 90°,
90°,  ranges between
ranges between
 min =
min =  (90°) =
(90°) =
 -1 and
-1 and  max =
max =
 (0°) = (1 +
(0°) = (1 +  )
) ~
2
~
2 for
for  >> 1.
Moreover,
>> 1.
Moreover,  = 1 for
= 1 for

 = arccos sqrt[(
= arccos sqrt[( - 1) / (
- 1) / ( + 1)]
(e.g., for an angle
+ 1)]
(e.g., for an angle 

 35° if
35° if  = 5), and for
decreasing
= 5), and for
decreasing 
 with increasing
with increasing
 (Fig. 20); for angles larger
than
(Fig. 20); for angles larger
than 
 relativistic deamplification takes place.
relativistic deamplification takes place.
Given a value of  , a lower
limit to the Lorentz
factor is given by the condition
, a lower
limit to the Lorentz
factor is given by the condition 

 max; that is,
max; that is,
When
which gives a useful upper limit to
In the relativistic beaming model, the observed transverse
velocity of an emitting blob, va =
It can be shown that if
The apparent velocity in terms of
We find from equations (A1) and (A4),
With a measurement of superluminal velocity and an independent estimate of the
Doppler factor (for example from an SSC calculation), one can combine Eqs.
(A1) and (A4) to obtain two equations in four unknowns. That is, under the
hypothesis that the ``bulk'' and ``pattern'' speeds are the same, one can
derive the value of the Lorentz factor and the angle to the line of sight:
Note that
The predicted jet/counter-jet ratio (i.e., the ratio between the
approaching and receding jets), can be expressed in terms of
In the simplest cases, p = 2 +
from which an upper limit to
It is useful to calculate the angular parameters relevant to tests
of unified schemes. For sources randomly oriented within the angular range
The linear size of extended sources is proportional to sin
Finally, the mean value of cos 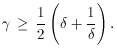
 is a lower limit, as in
the SSC case, this expression is valid
only for
is a lower limit, as in
the SSC case, this expression is valid
only for  > 1, since for
> 1, since for  < 1,
< 1,  + 1/
+ 1/ decreases
for increasing
decreases
for increasing  . It can also be
shown that for any value of
. It can also be
shown that for any value of  ,
,
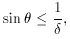
 if
if  > 1.
> 1.
 a c,
is related to its true velocity, v =
a c,
is related to its true velocity, v =  c, and the angle to the line of sight by
c, and the angle to the line of sight by
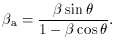
 > 1/
> 1/ 2
2  0.7, then for some
orientations superluminal motion is observed. The maximum value of the
apparent velocity,
0.7, then for some
orientations superluminal motion is observed. The maximum value of the
apparent velocity,  a, max = sqrt[
a, max = sqrt[ 2 -1], occurs when cos
2 -1], occurs when cos
 =
=  or sin
or sin  =
=  -1; for this angle,
-1; for this angle,  =
=
 . This implies a minimum value
for the Lorentz factor
. This implies a minimum value
for the Lorentz factor  min
= sqrt[
min
= sqrt[ a2 + 1] (see
Fig. 21). For
example, if one
detects superluminal motion in a source with
a2 + 1] (see
Fig. 21). For
example, if one
detects superluminal motion in a source with  a ~ 5,
the Lorentz factor responsible for it has to be at least 5.1. It is
also apparent from Fig. 21 that
superluminal speeds are
possible even for large angles to the line of sight; sources oriented at
a ~ 5,
the Lorentz factor responsible for it has to be at least 5.1. It is
also apparent from Fig. 21 that
superluminal speeds are
possible even for large angles to the line of sight; sources oriented at
 ~ 50°, have
~ 50°, have
 a
a
 2 if
2 if 
 5, and sources in the
plane of the sky (
5, and sources in the
plane of the sky ( = 90°) have
= 90°) have
 a =
a =  ~ 1 for
~ 1 for 
 3.
3.
 and
and  is
is
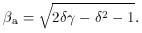
 a =
a = 

 sin
sin  , and for the angle that
maximizes the apparent velocity, sin
, and for the angle that
maximizes the apparent velocity, sin
 =
=  -1,
-1,  a
=
a
= 
 =
= 
 =
sqrt[
=
sqrt[ 2 -1]
2 -1] 


 .
.
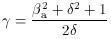
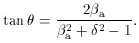
 reaches its minimum
value when
reaches its minimum
value when  = sqrt[
= sqrt[ a2
+ 1]
a2
+ 1] 
 min. If
min. If  is a lower limit (as when it is
derived from an SSC calculation)
and
is a lower limit (as when it is
derived from an SSC calculation)
and  < sqrt[
< sqrt[ a2
+ 1], then the
a2
+ 1], then the  estimated
from Eq. (A6) is an upper limit (of course always bound
to be
estimated
from Eq. (A6) is an upper limit (of course always bound
to be 
 min), while if
min), while if  >
sqrt[
>
sqrt[ a2 + 1], it is a
lower limit. For
a2 + 1], it is a
lower limit. For  >>
sqrt[
>>
sqrt[ a2 + 1],
a2 + 1], 

 / 2, while if
/ 2, while if  <<
sqrt[
<<
sqrt[ a2 + 1],
a2 + 1], 

 min/2
min/2  . As for Eq. (A7),
when
. As for Eq. (A7),
when  is a lower limit, the
inferred
is a lower limit, the
inferred  is always an upper
limit.
is always an upper
limit.
 and
and  a as
a as
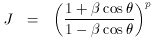
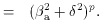
 or 3 +
or 3 +  (Appendix B).
Figure 22 shows the
jet/counter-jet
ratio as a function of the viewing angle for various values of the Lorentz
factors and for p = 2 (which minimizes the effect, as p is
likely to be
larger). The dependence on orientation is very strong,
since J
(Appendix B).
Figure 22 shows the
jet/counter-jet
ratio as a function of the viewing angle for various values of the Lorentz
factors and for p = 2 (which minimizes the effect, as p is
likely to be
larger). The dependence on orientation is very strong,
since J 
 2p. From the
jet/counter-jet ratio alone [Eq. (A8)], we obtain
2p. From the
jet/counter-jet ratio alone [Eq. (A8)], we obtain
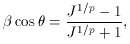
 (since
(since 
 1)
and a lower limit to
1)
and a lower limit to  (since cos
(since cos 
 1) can be derived.
1) can be derived.
 1 to
1 to  2, the mean orientation angle is
2, the mean orientation angle is
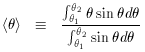
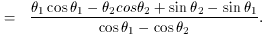
 , for which the mean value is
, for which the mean value is
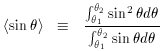
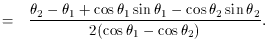
 is given by
is given by