


A. The Horizon Problem
Why is the universe so
homogeneous and isotropic on large scales? Radiation on opposite
sides of the observable universe today appear uniform in
temperature. Yet, there was not enough time in the past for the
photons to communicate their temperature to the opposing sides of
the visible universe (i.e., establish thermal equilibrium).
Consider the comoving radius of the causally connected parts of
the universe at the time of recombination compared to the comoving
radius at the present, found from Equation (6)
(remember c = 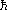 = 1).
= 1).
This means a much larger portion of the universe is visible today,
than was visible at recombination when the CBR was `released'. So
the paradox is how the CBR became homogeneous to 1 part in
105 as we discussed in Part II. There was no time for
thermal equilibrium to be reached. In fact, any region separated
by more than 2 degrees in the sky today would have been causally
disconnected at the time of decoupling
[29].
This argument can be made a bit more quantitative by consideration
of the entropy, S, which indicates the number of states within
the model. This can be used as a measure of the size of the
particle horizon
[5].
where mpl is the Planck mass, s is the entropy
density,
g* is the particle degeneracy, and z is the
redshift. These
equations for the entropy of the horizon in a radiation dominated
(43) and matter dominated universe (44),
are presented only to motivate the following estimates. For an
explanation please consult
[5].
At the time of recombination (z
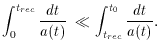
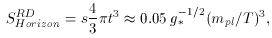
 1100), when the universe
was matter dominated, equation (44) gives a value of
about 1083 states. Compared with a value today of 1088
states, this is different by a factor of 105. Thus, there
are approximately 105 causally disconnected regions to be
accounted for in the observable universe today. The hot Big Bang
offers no resolution for this paradox, especially since it is
assumed to be an adiabatic (constant entropy) expansion.
1100), when the universe
was matter dominated, equation (44) gives a value of
about 1083 states. Compared with a value today of 1088
states, this is different by a factor of 105. Thus, there
are approximately 105 causally disconnected regions to be
accounted for in the observable universe today. The hot Big Bang
offers no resolution for this paradox, especially since it is
assumed to be an adiabatic (constant entropy) expansion.