6.1. Renormalization in Electrodynamics

Experimentalists and theoreticians have been gradually developing quantum electrodynamics (QED) since the late forties. Electrons and muons are excellent objects because, for them, all other interactions are much smaller than the electromagnetic ones.

The first approximation for muons and electrons in an atom or magnetic field is very simple; it is given by the Dirac theory. The electron, which has a spin, has a definite charge and magnetic moment also. However, various virtual processes must be accounted for in higher approximations. An electron in the ground state cannot emit a real photon - it does not have the required energy. But it can emit a photon and reabsorb it; this occurs in accordance with the Heisenberg uncertainty principle and does not violate energy conservation. One must imagine the creation and annihilation of "virtual" electron-positron pairs in the electrostatic field of the nucleus in the same way. These processes do not change the physical picture qualitatively: there is a precisely defined ground state, as well as an electrostatic field. Neither are emitting anything that could be detected by a distant observer (i.e., no free photons, electrons, or positrons are emitted). However, the exact quantitative properties of the ground state - the magnetic moment and the electrostatic field - are changed somewhat when the virtual processes are taken into account. These changes are small (more precisely, the equations for these corrections contain a small factor, since the electromagnetic interaction is relatively weak - e²/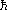c = 1/137, the so-called fine structure constant, is much less than unity). At first glance, the equations seem to contain infinite integrals because of the infinite number of possible virtual-particle states. Major scientific progress was made when it was realized that similar processes occur for both a free electron and an electron bound in, for example, a hydrogen atom. The measured quantity is the difference between the energy of a free electron and that of a bound electron, and the difference between the two infinite integrals is a finite integral. ⁽⁶⁾ The whole procedure, which was called renormalization, worked very well. The small effects in electrodynamics due to virtual processes (shift of bound states, change of magnetic moment) can now be calculated and measured to a precision of 10^-10 -10^-12 and no difference is observed between experiment and theory.

This is a very remarkable chapter in the history of modern physics, but we have described it here for a single modest purpose. The moral of the QED story is that virtual processes must not be neglected, since they do affect very real processes.

It now turned out that the beautiful story with the W^± and Z⁰ vector particles mediating in the weak interaction has one serious flaw.

One needs massive vector particles; their mass is needed to explain beta decay, etc.; their mass is measured at CERN - everything seems to be OK. But the searching spirit goes further. One begins to calculate the second-order correction, just as in electrodynamics, even though there is not yet any practical need to do so, the measurements are being far from exact enough.

But one cannot stop the logical development of the theory, for the QED example shows that the higher approximations are probably of real use. We now find that renormalization does not work for massive vector particles - one cannot get rid of the infinities!

The theory is in a self-created dead end. One needs mass to explain the role of the W and Z particles in the weak interaction, the mass is successfully measured - but the mass spoils the (not yet needed!) higher approximations.

⁶ Not always, of course, but at least in QED. Back.