


It is a truism that once the genie has been let out of the bottle, he never wants to go back inside . . . .
The successful use of the Higgs scalar field aroused a new,
long-lasting interest in scalar fields and their properties. The most important
mechanical properties used are the values of the energy density, energy
flux, momentum density, and stress in a given potential scalar field
distribution. We have already written down the law that describes the
evolution of the potential itself for the simplest case - flat, nonexpanding
Minkowski space. In the next section, we shall rewrite it for an
expanding universe with a "Friedman-Robertson-Walker" (FRW)
metric. In keeping with the idea of a homogeneous, isotropic universe,
we shall study the case of a scalar field
 that depends solely on
the world time t, i.e.,
that depends solely on
the world time t, i.e.,
 f(t). In accordance with the
homogeneous nature of the problem, the field does not depend on the space
coordinates. Since it is coordinate-independent,
f(t). In accordance with the
homogeneous nature of the problem, the field does not depend on the space
coordinates. Since it is coordinate-independent,
 can be used to
construct the time derivative d
can be used to
construct the time derivative d /
dt =
/
dt = 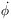 , but all the spatial
components of
the gradients ð
, but all the spatial
components of
the gradients ð /
ðx = ð
/
ðx = ð /
ðy =
ð
/
ðy =
ð / ðz = 0 are
identically equal to
zero, so that they do not define any preferred spatial direction. This is
in accordance with the fact that the space is isotropic and expanding.
It is clear from symmetry considerations that, in this case, the mechanical
properties of the field are described by two quantities - the energy
density
/ ðz = 0 are
identically equal to
zero, so that they do not define any preferred spatial direction. This is
in accordance with the fact that the space is isotropic and expanding.
It is clear from symmetry considerations that, in this case, the mechanical
properties of the field are described by two quantities - the energy
density  and p, the
isotropic pressure. (8)
and p, the
isotropic pressure. (8)
The first variant on the right-hand side of each equation is for the
simple case - a linear field equation - while the second variant, after
the "or," is written for a field with an arbitrary potential
V(
The first thing to realize is that the relation between the pressure and
the energy density is not unique. It is impossible to construct a definite
function p(
This is the stiffest possible equation of state.
(9) On the
other hand, if we
choose the combination
We retain the notation p (pressure) even though, in this case, it is in
fact isotropic tension along every spatial direction.
The fact that it is possible for the scalar field to produce tension
(i.e., negative pressure) is what makes it the most important field in
cosmology.
An electromagnetic field can produce tension along either the electric
field or the magnetic field. In the Faraday concept, field lines are
something like strained ropes. But this strain is more than compensated
for by the repulsion between the field lines in the direction
perpendicular to the field lines. A homogeneous electric or magnetic field
would produce a highly anisotropic pattern of tension and pressure; it
would make the expansion of the Universe anisotropic. A very tangled
field (which is easy to obtain with a magnetic field, but difficult to
obtain with an electric field) would produce an average positive
pressure p =
It is appropriate here to give several more extremely general
arguments that explain the negative pressure in the scalar field and,
especially, the relation p =
-
Condition (7.6) above means that
The fact that this tensor is invariant under the Lorentz transformation
is the essence of Einstein's statement about space and time. The
energy density and pressure are parts of the energy-momentum tensor
T
This idea was used to introduce the cosmological constant, which is
a way of expressing the assumption that the energy density of the
vacuum is not zero.
This idea was alien to classical physics, in which the "vacuum is a
place with nothing inside." However, in quantum physics, the vacuum
is merely the lowest state (that with minimum energy density); however,
the minimum of a function clearly does not necessarily occur at the zero
of the function. A definite value of the minimum energy must be
introduced so that the Lorentz invariance of the vacuum will not be
destroyed; this leads to
We just noted the observational fact that
We should also mention two other situations in the linear case.
For simplicity's sake, we shall return to the case of nonexpanding
Minkowski space. The equation for
The solution to (7.7) is
and we find that
and
The average pressure is zero on time intervals
A chaotic dependence of
The versatile nature of the scalar field is instructive. One can
construct a building, a cathedral, or a disordered set out of the same bricks;
the same is true of the scalar field and the corresponding particles.
Different situations are characterized by different pressure values,
ranging from p = -
8 For the reader familiar with the
interested in general relativity:
Tyx = Tzy =
Txz = 0.
The numerous zeros in the table of the Tki
are due to the choice of coordinate system: the
t = const hypersurface is chosen tangent to the
9 This equation of state was introduced
by the author in 1960 in a vain attempt to get
rid of stellar collapse. The main idea which inspired me, but which was
not stated in the
paper, was wrong: even an incompressible fluid experiences gravitational
collapse. But
the results derived remain: p =


 ) - for
example, the Higgs potential (see the preceding section).
) - for
example, the Higgs potential (see the preceding section).
 ). In
particular, the energy density is always positive. This
is clear in the linear case (the first variant) and this condition is imposed
on V(
). In
particular, the energy density is always positive. This
is clear in the linear case (the first variant) and this condition is imposed
on V( ) in the second case
(see the end of this section). The minimum,
Vmin(
) in the second case
(see the end of this section). The minimum,
Vmin( ) = 0, is a
reasonable condition; if this
condition were violated,
it would give the ground state nonzero energy. However, the energy
density
) = 0, is a
reasonable condition; if this
condition were violated,
it would give the ground state nonzero energy. However, the energy
density  > 0 can be
distributed between the "kinetic energy"
1/2
> 0 can be
distributed between the "kinetic energy"
1/2 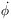 2 and
the potential energy differently in the excited state. There are two
limiting cases: all of the energy is in the form of kinetic energy. In this
case,
2 and
the potential energy differently in the excited state. There are two
limiting cases: all of the energy is in the form of kinetic energy. In this
case,


 = const,
i.e.,
= const,
i.e., 
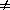 0 (or
0 (or

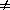
 min) and
min) and
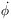 = 0, we then reach the
paradoxical situation
= 0, we then reach the
paradoxical situation

 /3
after averaging the pressure and tension. The same
equation of state is obtained for a gas of photons, neutrinos, or other
noninteracting highly relativistic particles. These well-known facts are
brought to the reader's attention for one purpose: to stress that the
ability to obtain isotropic tension [or large (in terms of absolute value)
negative quasihydrostatic pressure] is peculiar to the scalar field. This
is the basis of the inflationary cosmological models and is, therefore, of
the utmost importance for the remainder of the paper. The end of this
section is written for the mathematically oriented reader. Others may
go on to the next section without losing the thread of the argument.
/3
after averaging the pressure and tension. The same
equation of state is obtained for a gas of photons, neutrinos, or other
noninteracting highly relativistic particles. These well-known facts are
brought to the reader's attention for one purpose: to stress that the
ability to obtain isotropic tension [or large (in terms of absolute value)
negative quasihydrostatic pressure] is peculiar to the scalar field. This
is the basis of the inflationary cosmological models and is, therefore, of
the utmost importance for the remainder of the paper. The end of this
section is written for the mathematically oriented reader. Others may
go on to the next section without losing the thread of the argument.
 (7.5) for
(7.5) for

 ,
together with its derivative, is
invariant under the Lorentz transformation: both the spatial part,
grad3
,
together with its derivative, is
invariant under the Lorentz transformation: both the spatial part,
grad3  , and the
four-vector grad
, and the
four-vector grad  , which consists
of
, which consists
of 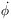 and grad3
and grad3  are equal to zero. This means that grad
are equal to zero. This means that grad
 does not point in any
particular direction in either space or time so that there is therefore no
preferred "rest frame." The "rest frame" is defined by zero energy (flux
and momentum). So (7.6) says, in effect, that all moving observers
should be unable to detect an energy flux or a field momentum. How
is this possible? If there is no flux in one frame and the density (at rest)
is
does not point in any
particular direction in either space or time so that there is therefore no
preferred "rest frame." The "rest frame" is defined by zero energy (flux
and momentum). So (7.6) says, in effect, that all moving observers
should be unable to detect an energy flux or a field momentum. How
is this possible? If there is no flux in one frame and the density (at rest)
is 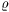 , a slowly moving
(v/c =
, a slowly moving
(v/c =  <<
1) observer would then observe a flux
<<
1) observer would then observe a flux
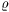 v. Because of the
equivalence principle, we can talk in terms of an
energy density
v. Because of the
equivalence principle, we can talk in terms of an
energy density  =
=
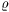 c2 and energy flux
c2 and energy flux
 v. However, we did
not take the
pressure into account. The total energy flux consists of the mass flux
v. However, we did
not take the
pressure into account. The total energy flux consists of the mass flux
 v
plus a second term, the work done by the pressure pv, so that
j = (
v
plus a second term, the work done by the pressure pv, so that
j = ( +
p)v. We magically see that p =
-
+
p)v. We magically see that p =
- is precisely the condition
for j = 0 in all moving frames of reference. The condition v
<< c is not
binding: if j = 0 is valid for small v, then, by adding
several small v,
we obtain j = 0 for all finite v < c, provided, of course,
that the
condition p = -
is precisely the condition
for j = 0 in all moving frames of reference. The condition v
<< c is not
binding: if j = 0 is valid for small v, then, by adding
several small v,
we obtain j = 0 for all finite v < c, provided, of course,
that the
condition p = - is
satisfied. We shall finally give a formal proof that
dates back to the early days of relativity: the local Minkowski metric is
characterized by the diagonal metric tensor g00 = 1,
g11 = g22
= g33 = - 1 (with all other
g
is
satisfied. We shall finally give a formal proof that
dates back to the early days of relativity: the local Minkowski metric is
characterized by the diagonal metric tensor g00 = 1,
g11 = g22
= g33 = - 1 (with all other
g

 0).
0).

 , which is also a
second-rank tensor, like the
metric tensor g
, which is also a
second-rank tensor, like the
metric tensor g
 . To
be invariant under the Lorentz transformation, the
T
. To
be invariant under the Lorentz transformation, the
T
 must be
proportional to the g
must be
proportional to the g
 , which, in
everyday language, reduces to (7.5).
, which, in
everyday language, reduces to (7.5).
 v =
-pv = 0 (the subscript v stands for
vacuum). From astronomical observations, we know that
v =
-pv = 0 (the subscript v stands for
vacuum). From astronomical observations, we know that
 v and
pv are
extremely small (even values of zero are not excluded). A straight-forward
evaluation of
v and
pv are
extremely small (even values of zero are not excluded). A straight-forward
evaluation of  v
using quantum field theory yields
v
using quantum field theory yields
 v ~ ±
1093 erg cm-3. This
very precise cancellation requires a special
explanation that has not yet been found - but this is another story.
v ~ ±
1093 erg cm-3. This
very precise cancellation requires a special
explanation that has not yet been found - but this is another story.
 v and
pv are almost exactly
equal to zero. Now, we turn to the scalar field. A region of space with
a nonzero (or nonminimum) value of
v and
pv are almost exactly
equal to zero. Now, we turn to the scalar field. A region of space with
a nonzero (or nonminimum) value of  is not a vacuum! However, if
all of the derivatives
is not a vacuum! However, if
all of the derivatives 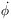 ,
grad3
,
grad3  are equal to zero, this
state then has the same symmetry as the vacuum, so that p =
-
are equal to zero, this
state then has the same symmetry as the vacuum, so that p =
- ; in this case, the ratio
p /
; in this case, the ratio
p /  = -1, just as
for a vacuum, but the absolute values of p and
= -1, just as
for a vacuum, but the absolute values of p and
 are
quite different from pv and
are
quite different from pv and
 v. This is the
end of our discussion of
whether or not large negative pressure is possible in a scalar field.
v. This is the
end of our discussion of
whether or not large negative pressure is possible in a scalar field.
 in the uniform case, in which it
is independent of x, y, and z, is
in the uniform case, in which it
is independent of x, y, and z, is




 such that
µ
such that
µ >> 1. The
average field describes a collection of particles at rest, so there is,
naturally, some energy, but the pressure is zero.
>> 1. The
average field describes a collection of particles at rest, so there is,
naturally, some energy, but the pressure is zero.
 on x,
y, and z can describe scalar particles
in thermal equilibrium. In this case, the average pressure varies from
p <<
on x,
y, and z can describe scalar particles
in thermal equilibrium. In this case, the average pressure varies from
p <<  for thermal
energies much less than the rest mass of the particles
to p =
for thermal
energies much less than the rest mass of the particles
to p =  /3 at high
temperature, when we are dealing with an extreme
relativistic gas of scalar particles.
/3 at high
temperature, when we are dealing with an extreme
relativistic gas of scalar particles.
 to p = +
to p = + ; the
pressure can, in some cases, be
anisotropic. The energy density is always positive, unlike the pressure.
The last point is more linguistic than physical. In macroscopic physics
(say, hydrodynamics or elasticity), the notion of pressure can only be
used for relaxed systems, just like the notion of "equation of state",
p = p(
; the
pressure can, in some cases, be
anisotropic. The energy density is always positive, unlike the pressure.
The last point is more linguistic than physical. In macroscopic physics
(say, hydrodynamics or elasticity), the notion of pressure can only be
used for relaxed systems, just like the notion of "equation of state",
p = p(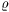 ) or
p = p(
) or
p = p(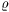 ,
S) (where S is the entropy). The stress tensor in
a nonrelaxed system is usually written as the sum of a pressure and
a viscosity term. In the case of the scalar field and, in particular, the
homogeneous field
,
S) (where S is the entropy). The stress tensor in
a nonrelaxed system is usually written as the sum of a pressure and
a viscosity term. In the case of the scalar field and, in particular, the
homogeneous field  =
=
 (t), the system is obviously not
relaxed, and
not in thermodynamic equilibrium (one can obtain more entropy at a
given energy density by introducing many incoherent waves). This
means that our use of the word "pressure" is a linguistic
oversimplification.
(t), the system is obviously not
relaxed, and
not in thermodynamic equilibrium (one can obtain more entropy at a
given energy density by introducing many incoherent waves). This
means that our use of the word "pressure" is a linguistic
oversimplification.
 =
T00, -p =
Tyy
Tzz, T0x =
T0y = T0z = 0,
=
T00, -p =
Tyy
Tzz, T0x =
T0y = T0z = 0,
 = const hypersurface. Therefore, all
spatial derivatives are zero at the point of observation, and there is
no preferred direction.
In a cosmological solution with uniform
= const hypersurface. Therefore, all
spatial derivatives are zero at the point of observation, and there is
no preferred direction.
In a cosmological solution with uniform
 , the two hypersurfaces are
not only tangent
at one point but also identical throughout all space. This is not always
possible. The best
example is the static (time-independent) but strongly nonhomogeneous
, the two hypersurfaces are
not only tangent
at one point but also identical throughout all space. This is not always
possible. The best
example is the static (time-independent) but strongly nonhomogeneous
 field between
two charges at rest. The
field between
two charges at rest. The  = const
hypersurface is time-like; there is no tangent space-like
t = const hypersurface at any point. In a coordinate system where
everything is at
rest the energy density
= const
hypersurface is time-like; there is no tangent space-like
t = const hypersurface at any point. In a coordinate system where
everything is at
rest the energy density  =
1/2 (grad3
=
1/2 (grad3  )2 +
V(
)2 +
V( ), and there is no
momentum or energy
flux; this is obvious in a static system. What is most important is that
the stress is highly
anisotropic. Taking the x-axis along the field gradient,
ð
), and there is no
momentum or energy
flux; this is obvious in a static system. What is most important is that
the stress is highly
anisotropic. Taking the x-axis along the field gradient,
ð / ðx = g,
ð
/ ðx = g,
ð / ðy =
ð
/ ðy =
ð / ðz - 0,
we obtain compression along the x-axis
(Txx = V - 1/2 g2)
and tension along the y- and
z-axes (Tyy =
Tzz
= V + 1/2 g2). The case of vanishing
V(
/ ðz - 0,
we obtain compression along the x-axis
(Txx = V - 1/2 g2)
and tension along the y- and
z-axes (Tyy =
Tzz
= V + 1/2 g2). The case of vanishing
V( ) is
similar to the Coulomb electrostatic field of an electric charge at rest,
) is
similar to the Coulomb electrostatic field of an electric charge at rest,
 = e/r. But
the sign of the pressure and
tension are reversed for the scalar field relative to the electrostatic
case: Txx = E2 /
8
= e/r. But
the sign of the pressure and
tension are reversed for the scalar field relative to the electrostatic
case: Txx = E2 /
8 ,
Tyy = Tzz =
-E2 / 8
,
Tyy = Tzz =
-E2 / 8 (For an E
along the x-axis, the
electrostatic field depends on x
alone). The change in sign of the stress tensor reflects the fundamental
difference between
the scalar and electrostatic fields: attraction of equal charges for the
scalar field and
repulsion of equal charges for the electrostatic field.
Back.
(For an E
along the x-axis, the
electrostatic field depends on x
alone). The change in sign of the stress tensor reflects the fundamental
difference between
the scalar and electrostatic fields: attraction of equal charges for the
scalar field and
repulsion of equal charges for the electrostatic field.
Back.
 =
=
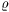 c2 is the
equation of state corresponding to a sound
velocity equal to c, the speed of light. The equation of state
for an extreme relativistic gas,
p =
c2 is the
equation of state corresponding to a sound
velocity equal to c, the speed of light. The equation of state
for an extreme relativistic gas,
p =  /3, T =
T
/3, T =
T
 =
=
 - 3p = 0, is not
the limit. A ratio of pressure to energy density
greater than 1/3 is possible: it can be as large as 1.
Back.
- 3p = 0, is not
the limit. A ratio of pressure to energy density
greater than 1/3 is possible: it can be as large as 1.
Back.