Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
311-358 Copyright © 1992 by Annual Reviews. All rights reserved |
where we have introduced an effective lens distance D. An
off-axis source will produce two images on opposite sides of the
lens - a magnified image outside the Einstein ring, and one inside
with magnification diminishing as (
where the subscripts 1 and 2 refer to components along two orthogonal
axes. The associated magnification matrix of such a quadratic
lens is
where
For source positions
3.2 Simple Lens Models
 relative to a
point mass M is given by
relative to a
point mass M is given by  hat (
hat ( ) = 4GM
) = 4GM / c2
/ c2 2.
A source on the optic axis will form an Einstein
ring
(Chwolson 1924,
Einstein 1936)
of angular radius
2.
A source on the optic axis will form an Einstein
ring
(Chwolson 1924,
Einstein 1936)
of angular radius
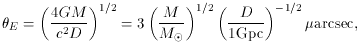
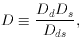
 E /
E /  )4 for
)4 for
 >>
>>  E.
For source positions
E.
For source positions 

 E the two images
have roughly comparable magnifications. Therefore, the effective
cross section for lensing is usually taken to be
E the two images
have roughly comparable magnifications. Therefore, the effective
cross section for lensing is usually taken to be 
 E2. Using this estimate of the cross
section, the optical depth to lensing for a point source at high
redshift is of order the fractional mass density
E2. Using this estimate of the cross
section, the optical depth to lensing for a point source at high
redshift is of order the fractional mass density  0 of the
universe in point mass lenses
(Press & Gunn
1973).
For extended sources of angular size
0 of the
universe in point mass lenses
(Press & Gunn
1973).
For extended sources of angular size 
 E, this is also the optical
depth corresponding to significant image distortion due to lensing.
E, this is also the optical
depth corresponding to significant image distortion due to lensing.
 E
and thus estimate the mass M of the lens
``enclosed'' by the images. Further, for
non-point-like lenses, the optical depth to lensing for a high
redshift source is roughly given by the density parameter
E
and thus estimate the mass M of the lens
``enclosed'' by the images. Further, for
non-point-like lenses, the optical depth to lensing for a high
redshift source is roughly given by the density parameter  E
corresponding to the fractional lens mass enclosed within the
respective Einstein rings of the lenses.
E
corresponding to the fractional lens mass enclosed within the
respective Einstein rings of the lenses.
 to
quadratic order and rotate the coordinate system so that
to
quadratic order and rotate the coordinate system so that
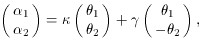
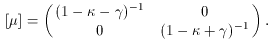
 is the
convergence, which measures the
isotropic part of the magnification:
is the
convergence, which measures the
isotropic part of the magnification:
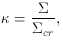
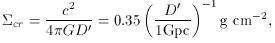
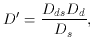
 cr is
known as the critical density and
D' = D (Dds / Ds)2 is a second
effective lens distance. Normally
a lens will have
cr is
known as the critical density and
D' = D (Dds / Ds)2 is a second
effective lens distance. Normally
a lens will have  >
>  cr somewhere in order
to produce multiple images, but this is not strictly necessary
(Subramanian &
Cowling 1986).
The parameter
cr somewhere in order
to produce multiple images, but this is not strictly necessary
(Subramanian &
Cowling 1986).
The parameter  is known as
the shear and measures the anisotropic stretching of the image.
It arises from matter lying outside the beam. Quadratic lenses are
used to describe background galaxies surrounding individual stars and
sometimes also for galaxy clusters around galaxies.
is known as
the shear and measures the anisotropic stretching of the image.
It arises from matter lying outside the beam. Quadratic lenses are
used to describe background galaxies surrounding individual stars and
sometimes also for galaxy clusters around galaxies.
 = 300
= 300 300 km
s-1. For a singular isothermal sphere, the deflection
angle is constant and given by
300 km
s-1. For a singular isothermal sphere, the deflection
angle is constant and given by  hat = 4
hat = 4
 2 /
c2 = 2.6"
2 /
c2 = 2.6"  2300, so
that
2300, so
that
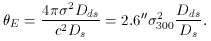
 <
<  E,
there are two images at
E,
there are two images at
 =
=  ±
±  E. Technically, there is also a third
image at
E. Technically, there is also a third
image at  = 0, but this
has zero magnification because the
surface density is singular at the center of the lens. The
cross section for multiple-imaging is given by
= 0, but this
has zero magnification because the
surface density is singular at the center of the lens. The
cross section for multiple-imaging is given by 
 E2.
E2.
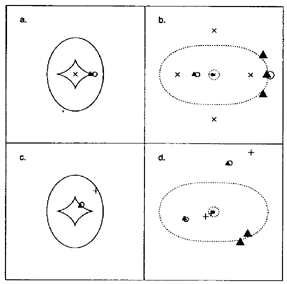
Figure 6. Multiple imaging of point sources at fixed
redshift by a generic ``elliptical lens''. The solid lines in the left
panels are caustics that separate regions in the source plane
corresponding to different image multiplicities (1, 3, and 5 as
indicated). The inner caustic, sometimes referred to as the
tangential caustic, has four cusps connected by fold lines. The
outer radial caustic is a pure fold. The outer dashed lines in
the right panels are tangential critical curves and the inner ones are
radial critical curves. The symbols show representative source
positions and the corresponding image locations. When the source is
close to a caustic, some of the images are strongly magnified,
indicated by large symbols in the image panels. One of the multiple
images usually occurs near the center of the lens and is strongly
demagnified if the core radius of the lens is small. Among the
``secure'' multiple quasars, Q1413+117 and
Q2237+031 correspond to the
source position x and Q0142-100 to O in the upper panels.
Q0414+053
and Q1115+080 correspond to the triangle and
Q0957+561
is midway
between O and + in the lower panels. The weak central image has not
been seen in any of the observed cases.
 c such that the deflection angle is diminished
for
c such that the deflection angle is diminished
for  <
<  c
and vanishes for
c
and vanishes for  = 0. The surface density
= 0. The surface density  c
at the center of the lens now is finite, and multiple imaging is
possible only if
c
at the center of the lens now is finite, and multiple imaging is
possible only if  c exceeds the (distance-dependent) critical
density
c exceeds the (distance-dependent) critical
density  cr. When there is multiple imaging, in addition
to two images on either side of the lens as in the singular isothermal
lens, there is also a third image in the core region which for small
cr. When there is multiple imaging, in addition
to two images on either side of the lens as in the singular isothermal
lens, there is also a third image in the core region which for small
 c is
usually weak in comparison to the other two. (b) It
is often essential to break the circular symmetry of the lens. This
can be done by introducing a quadrupolar component in either the mass
distribution or the potential of the lens, or by adding an external
shear to a circularly symmetric lens. We refer to such models as
elliptical lenses. Figures 6 and 7 show some image configurations
that arise with elliptical lenses in front of point and extended
sources.
c is
usually weak in comparison to the other two. (b) It
is often essential to break the circular symmetry of the lens. This
can be done by introducing a quadrupolar component in either the mass
distribution or the potential of the lens, or by adding an external
shear to a circularly symmetric lens. We refer to such models as
elliptical lenses. Figures 6 and 7 show some image configurations
that arise with elliptical lenses in front of point and extended
sources.

Figure 7. Representative arc and ring images of resolved
sources produced by an elliptical lens. In each set, the source planes
are on the left and the corresponding images are on the right. The
long luminous arcs in Abell 370, Cl 2244-02,
Abell 963 and other
clusters are similar to the case displayed at top right. (The
counter-image shown here will not be present for certain choises of
the lens parameters; see
Narayan &
Grossman 1989,
Narayan &
Wallington 1992a.)
The radio rings correspond to the case shown at bottom right,
and the incomplete ring in MG1131+0456 at 15 GHz is similar to the
example at bottom left.