Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
311-358 Copyright © 1992 by Annual Reviews. All rights reserved |
The real part of D1 measures the expansion of the ray
while its imaginary part describes pure rotation. (In practice,
rotation is usually small and D1 is approximately real.)
D2 measures the shear. All the information about the local
image distortion is contained in D. The conventional angular
diameter distance, whose square is the ratio of the source area to the
solid angle it subtends, is given by [| D1 | 2 -
| D2 | 2] 1/2, and suffices for point
sources where only the flux can be measured.
where the quantity R = -(1 + z)2(
3.3 Caustics and Congruences
 (
( )=(
)=( 1,
1,  2), equal
to this offset as measured all
along the bundle, not just in the lens plane. The subscripts 1, 2
represent components with respect to an orthonormal basis parallel
propagated along the fiducial ray, and
2), equal
to this offset as measured all
along the bundle, not just in the lens plane. The subscripts 1, 2
represent components with respect to an orthonormal basis parallel
propagated along the fiducial ray, and  is the affine
parameter. Next, define the complex number
is the affine
parameter. Next, define the complex number
 (
( ) =
) =  1 +
i
1 +
i  2. The angle between a ray in the
congruence and the fiducial ray at the observer can also be
represented as a complex number dot
2. The angle between a ray in the
congruence and the fiducial ray at the observer can also be
represented as a complex number dot 0, where a dot denotes
differentiation with respect to
0, where a dot denotes
differentiation with respect to  . We are now in a position
to generalize the notion of angular diameter distance by defining a
two component vector, D =
(D1, D2), where both
D1 and D2 are complex, using the
general linear relation
. We are now in a position
to generalize the notion of angular diameter distance by defining a
two component vector, D =
(D1, D2), where both
D1 and D2 are complex, using the
general linear relation
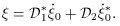
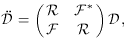
 ,11 +
,11 +  ,22) =
-4
,22) =
-4 (1 +
z)2G
(1 +
z)2G describes focusing by matter lying within the
congruence with pr oper density
describes focusing by matter lying within the
congruence with pr oper density  , and F = -(1 + z)2(
, and F = -(1 + z)2( ,11 -
,11 -  ,22 + 2i
,22 + 2i  ,12) describes the
influence of matter external to the congruence (e.g.
Penrose 1966,
Blandford et
al. 1991).
This formalism immediately gives expressions for the
magnification tensors, [µ] (cf Equation 3), whose definition we
can now generalize by identifying
,12) describes the
influence of matter external to the congruence (e.g.
Penrose 1966,
Blandford et
al. 1991).
This formalism immediately gives expressions for the
magnification tensors, [µ] (cf Equation 3), whose definition we
can now generalize by identifying  with the angle which
would be subtended by the proper length
with the angle which
would be subtended by the proper length  in the source plane in a
FRW universe of similar average density to the inhomogeneous
universe under consideration. (See
Ehlers &
Schneider 1986
for an alternative choice of reference universe).
in the source plane in a
FRW universe of similar average density to the inhomogeneous
universe under consideration. (See
Ehlers &
Schneider 1986
for an alternative choice of reference universe).
 0 increases the angular diameter
distance of the source
(Dashevskii &
Zel'dovich 1965,
Dyer & Roeder 1972,
Nottale 1983,
Nottale & Hammer
1984,
Kasai et
al. 1990).
The increase is about 30 per cent for a source
with zs ~ 2 in an Einstein-De Sitter universe.
However, the cumulative
shear caused by external matter usually produces a second order
focusing which leads to a diminished net effect. In general, if
multiple imaging is uncommon, the distribution of magnifications due
to smoothly distributed matter is dominated by the convergence rather
than shear
(Lee & Paczynski
1990,
Watanabe &
Sasaki 1990).
The total flux is always conserved when suitably averaged over all
directions
(Weinberg 1976,
Peacock 1986).
0 increases the angular diameter
distance of the source
(Dashevskii &
Zel'dovich 1965,
Dyer & Roeder 1972,
Nottale 1983,
Nottale & Hammer
1984,
Kasai et
al. 1990).
The increase is about 30 per cent for a source
with zs ~ 2 in an Einstein-De Sitter universe.
However, the cumulative
shear caused by external matter usually produces a second order
focusing which leads to a diminished net effect. In general, if
multiple imaging is uncommon, the distribution of magnifications due
to smoothly distributed matter is dominated by the convergence rather
than shear
(Lee & Paczynski
1990,
Watanabe &
Sasaki 1990).
The total flux is always conserved when suitably averaged over all
directions
(Weinberg 1976,
Peacock 1986).
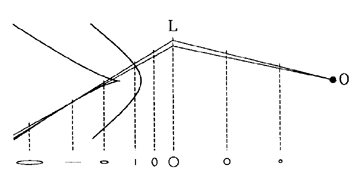
Figure 8. An infinitesimal conical bundle of rays is shown
drawn backwards from an observer, past an elliptical lens, and
touching two caustic sheets. The second caustic sheet, on the left,
has a cusp line perpendicular to the plane of the diagram, while the
first caustic sheet has a cusp in the plane. Representative cross
sections of the bundle are indicated at the bottom. Where the bundle
touches a caustic, its cross section degenerates to a straight
line. Beyond this point, the bundle is ``inverted'' and a source
located here will acquire two additional images. In general there
could be many caustic sheets behind a complex lens, but with a single
elliptical lens there are only two sheets (which may penetrate each
other, cf Blandford & Narayan 1986).
 ( > µ), for the magnification to be greater than
µ has a universal scaling,
( > µ), for the magnification to be greater than
µ has a universal scaling, 
 µ-2,
for µ >> 1.
Equivalently, the differential cross section scales as d
µ-2,
for µ >> 1.
Equivalently, the differential cross section scales as d / dµ
/ dµ
 µ-3.
µ-3.
 (> µ)
(> µ)  µ-5/2, or d
µ-5/2, or d /dµ
/dµ  µ-7/2. Cusps are believed to play
an important role in the
luminous arcs. Cusp lines meet at points associated with higher
order singularities, but these have not yet been identified in the
observations. The closest point of the caustic to the observer is
generically a cusp. When a source is located close to this point,
the lens is said to be marginal and may produce one or three
bright images
(Narayan et
al. 1984,
Kovner 1987d,
e).
µ-7/2. Cusps are believed to play
an important role in the
luminous arcs. Cusp lines meet at points associated with higher
order singularities, but these have not yet been identified in the
observations. The closest point of the caustic to the observer is
generically a cusp. When a source is located close to this point,
the lens is said to be marginal and may produce one or three
bright images
(Narayan et
al. 1984,
Kovner 1987d,
e).