


Bottema (1993), from an analysis of velocity dispersions, claims that the maximum velocity of the disc component is 63% of the maximum observed velocity. The path to this result is strewn with assumptions, the most important of which are that discs are exponential with a velocity ellipsoid close to that in the solar neighbourhood, that Freeman's (1970) law holds, and that (B - V)old disc = 0.7 for all discs. As already discussed above, for NGC 3198 Bottema's result corresponds closely to the ``no m = 2'' solution proposed by Athanassoula et al. (1987).
A quick re-evaluation of Bottema's result can be formulated as
follows. From the good agreement between the stellar and gas
rotation data presented in
Bottema (1988),
it follows that the asymmetric drift in NGC 3198 is small, and thus the epicyclic
approximation can be used. This states that  / 2
/ 2 =
=

 /
/ R, where
R, where
 is the angular
velocity,
is the angular
velocity,  is the epicyclic
frequency, and
is the epicyclic
frequency, and  R
and
R
and 
 are respectively the
radial and
azimuthal velocity dispersion. From the measurement of the
rotation curve and the velocity dispersion along the major axis,
ignoring the z-axis contribution for the moment, we can then calculate
the radial velocity dispersion
are respectively the
radial and
azimuthal velocity dispersion. From the measurement of the
rotation curve and the velocity dispersion along the major axis,
ignoring the z-axis contribution for the moment, we can then calculate
the radial velocity dispersion  R as function of radius,
and from the mass model we can calculate the critical radial velocity
dispersion needed for axisymmetric stability. The ratio between these two is
Toomre's (1964)
parameter Q:
R as function of radius,
and from the mass model we can calculate the critical radial velocity
dispersion needed for axisymmetric stability. The ratio between these two is
Toomre's (1964)
parameter Q:
For NGC 3198 we then find for the ``maximum disc'' model a mean
Q of 0.92, and for a ``no m = 2'' model a mean Q of 1.92. The real
uncertainties in these values are about 20%. The important result
is that indeed for NGC 3198 the measured velocity dispersion seems
too low to have a stable ``maximum disc'' solution (see also Fuchs's
contribution in this volume).
One can argue with this in several ways. First of all, the
observed major axis velocity dispersion is a combination of
Second, the numerical
factor 3.36, which corresponds to a Schwarzschild distribution of
the random velocities in an infinitesimally thin disc, should perhaps be
corrected for the effect of thickness, possibly also for a different
shape of the distribution function, and certainly for the effect of
the gas which is important for a late type spiral. The thickness
correction alone (calculated assuming all the material in the disc,
and the solar neighbourhood value for the ratio of vertical to
radial velocity dispersions) lowers the numerical factor to 2.6
(cf.
Shu 1968,
Vandervoort 1970)
and the effect of 10% of gas
enhances then the factor to about 2.9 (cf.
Toomre 1974).
Other distribution functions may apply:
Fuchs & Von Linden
(1998)
rediscuss and extend work by
Graham (1967)
and by Toomre (unpublished)
on an exponential distribution function, for which the
numerical factor is 3.944 instead of 3.36, so that with the
thickness and 10% gas corrections we end up at 3.40. From
Graham's (1967)
Figure 1, where he
shows results for several
other distribution functions, it becomes clear that the uncertainty
in the numerical factor could be easily 20-30%.
Finally, as
argued by Kormendy (priv. comm., see also discussion after Fuchs's
contribution), the influence of younger stellar populations in the
spectra could result in lower measured velocity dispersions. In
view of all these arguments, perhaps we should not be overly
worried about the result that Q is just below 1.00 in NGC 3198.
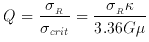

 and
and  z, so the determination of
z, so the determination of
 R may not be
entirely correct.
R may not be
entirely correct.