Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
499-542 Copyright © 1992 by Annual Reviews. All rights reserved |
3.4 Comoving Density of Objects
One is sometimes able to count objects (e.g. galaxies) in observable
volume elements, that is, per solid angle d and per redshift interval
dz. If the objects counted can be identified with objects of a known
comoving density (e.g. galaxies today), then one has in effect another
distance measure in the relation between comoving density and
redshift, and another opportunity to learn about
and per redshift interval
dz. If the objects counted can be identified with objects of a known
comoving density (e.g. galaxies today), then one has in effect another
distance measure in the relation between comoving density and
redshift, and another opportunity to learn about
 M,
M,

 . The comoving
volume element of the Friedmann-Robertson-Walker metric is
. The comoving
volume element of the Friedmann-Robertson-Walker metric is
Notice that the volume element is not simply a function of
dM, or of
dM and z, but has an additional dependence on
Equation 26 has the consequence that, given a population of objects
of constant (or calibratable) density and determinable distance
measures, one can in principle directly measure
More model-dependently, one can calculate from Equations 26 and 25
the dependence of dV on z, and use observed number counts
to constrain
the values of
Equation 26 can be integrated analytically to give the comoving
volume out to a distance dM,
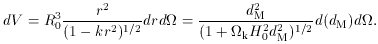
 k. This shows that
number counts fundamentally probe a different aspect of the universe's
geometry than do the distance measures of Equation 22.
k. This shows that
number counts fundamentally probe a different aspect of the universe's
geometry than do the distance measures of Equation 22.
 k (or
k (or
 tot) and
determine whether the universe is open or closed, in an almost
model-independent fashion: One ``simply'' determines (e.g. along a
pencil beam) whether the volume V scales as
dM3, or whether it shows
evidence of the denominator in Equation 26. If dM, the
proper motion
distance, were directly accessible to measurement, this test could be
performed without measuring any redshifts! Unfortunately,
dM is the
least accessible of distance measures. Using dL or
dA instead, the
test requires that redshifts be known, or estimated from a model of
the sources (as in
Sandage 1988).
tot) and
determine whether the universe is open or closed, in an almost
model-independent fashion: One ``simply'' determines (e.g. along a
pencil beam) whether the volume V scales as
dM3, or whether it shows
evidence of the denominator in Equation 26. If dM, the
proper motion
distance, were directly accessible to measurement, this test could be
performed without measuring any redshifts! Unfortunately,
dM is the
least accessible of distance measures. Using dL or
dA instead, the
test requires that redshifts be known, or estimated from a model of
the sources (as in
Sandage 1988).
 M,
M,
 tot
(Loh 1986).
Figure 6 shows how the comoving
volume element dV / dz
d
tot
(Loh 1986).
Figure 6 shows how the comoving
volume element dV / dz
d varies with z for the
five models A-E. Notice
that at modest redshifts (e.g. z = 1/2) the fractional variation among
the models is significantly larger in Figure 6
than for the other distance measures in
Figure 5.
This is an attractive feature of number
count tests, but (as we will see) it must be weighed against their
susceptibility to evolutionary and selection effects. At redshifts 1 +
z ~ 2, the models with significant
varies with z for the
five models A-E. Notice
that at modest redshifts (e.g. z = 1/2) the fractional variation among
the models is significantly larger in Figure 6
than for the other distance measures in
Figure 5.
This is an attractive feature of number
count tests, but (as we will see) it must be weighed against their
susceptibility to evolutionary and selection effects. At redshifts 1 +
z ~ 2, the models with significant

 have volumes-per-redshift larger
than the open models by a factor ~ 2, and larger than the flat
have volumes-per-redshift larger
than the open models by a factor ~ 2, and larger than the flat
 M = 1
model by a factor ~ 4. This results in
M = 1
model by a factor ~ 4. This results in
 -models becoming fashionable
whenever excess counts of high-redshift objects are claimed to exist
(see Section 4.3 below).
-models becoming fashionable
whenever excess counts of high-redshift objects are claimed to exist
(see Section 4.3 below).