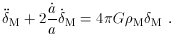2.4 Structure formation
The introduction of a cosmological constant changes the relationship between the matter density and expansion rate from what it would be in a matter-dominated universe, which in turn influences the growth of large-scale structure. The effect is similar to that of a nonzero spatial curvature, and complicated by hydrodynamic and nonlinear effects on small scales, but is potentially detectable through sufficiently careful observations.
The analysis of the evolution of structure is greatly abetted by the fact that perturbations start out very small (temperature anisotropies in the microwave background imply that the density perturbations were of order 10-5 at recombination), and linearized theory is effective. In this regime, the fate of the fluctuations is in the hands of two competing effects: the tendency of self-gravity to make overdense regions collapse, and the tendency of test particles in the background expansion to move apart. Essentially, the effect of vacuum energy is to contribute to expansion but not to the self-gravity of overdensities, thereby acting to suppress the growth of perturbations [11, 3].
For sub-Hubble-radius perturbations in a cold dark matter component, a Newtonian analysis suffices. (We may of course be interested in super-Hubble-radius modes, or the evolution of interacting or relativistic particles, but the simple Newtonian case serves to illustrate the relevant physical effect.) If the energy density in dynamical matter is dominated by CDM, the linearized Newtonian evolution equation is
The second term represents an effective frictional force due to
the expansion of the universe, characterized by a timescale
(
where H(a) is given by (30). There exist analytic
approximations to this formula
[3], as well as
analytic expressions for flat universes
[26].
Note that this analysis is
consistent only in the linear regime; once perturbations on a given
scale become of order unity, they break away from the Hubble flow
and begin to evolve as isolated systems.
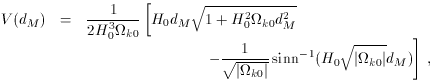
/ a)-1 =
H-1, while the right hand side is a forcing
term with characteristic timescale (4
G
M)-1/2
M-1/2
H-1. Thus, when
M
1, these effects are in
balance and CDM perturbations gradually grow; when
M dips appreciably below
unity (as when curvature or vacuum energy begin to dominate),
the friction term becomes more important and perturbation growth
effectively ends. In fact (45) can be directly
solved
[25] to yield
