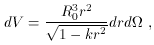2.3 Surveying the universe
The lookback time from the present day to an object at redshift z* is given by
with H(a) given by (30).
The age of the universe is obtained by taking the
z* ->
Figure 2. Expansion histories for different
values of
In a generic curved spacetime, there is no preferred notion of
the distance between two objects. Robertson-Walker spacetimes
have preferred foliations, so it is possible to define sensible
notions of the distance between comoving objects - those whose
worldlines are normal to the preferred slices. Placing ourselves
at r = 0 in the coordinates defined by (2), the
coordinate distance r to another comoving object is independent
of time. It can be converted to a physical distance at any
specified time t* by multiplying by the scale factor
R0 a(t*),
yielding a number which will of course change as the universe
expands. However, intervals along spacelike slices are not
accessible to observation, so it is typically more convenient to
use distance measures which can be extracted from observable
quantities. These include the luminosity distance,
whereL is the intrinsic luminosity and F the measured
flux; the proper-motion distance,
where u is the transverse proper velocity and
where D is the proper size of the object and
The three measures are related by
so any one can be converted to any other for sources of known
redshift.
The proper-motion distance between sources at redshift z1
and z2 can
be computed by using ds2 = 0 along a light ray, where
ds2
is given by (2). We have
where we have used (5) to solve for R0 = 1 /
(H0
The comoving volume element in a Robertson-Walker universe
is given by
which can be integrated analytically to obtain the volume
out to a distance dM:
where ``sinn'' is defined as below (42).
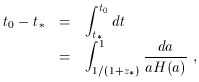
(t* -> 0) limit. For
=
M = 1, this yields
the familiar answer
t0 = (2/3) H0-1; the age
decreases as M
is increased, and increases as 
is
increased.
Figure (2) shows the expansion history of the universe
for different values of these parameters and H0 fixed; it
is clear how the acceleration caused by
leads
to an older universe. There are analytic approximation formulas which estimate
(36) in various regimes
[10,
11,
3], but generally
the integral is straightforward to perform numerically.
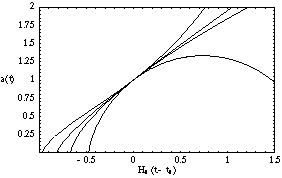
M and
. From top to bottom,
the curves describe
(M,
) =
(0.3, 0.7), (0.3, 0.0), (1.0, 0.0), and (4.0, 0.0).
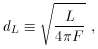
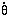the
observed angular velocity; and the angular-diameter distance,
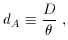
its
apparent angular size. All of these definitions reduce to the
usual notion of distance in a Euclidean space. In a
Robertson-Walker universe,
the proper-motion distance turns out to equal the physical
distance along a spacelike slice at t = t0:
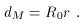
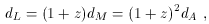
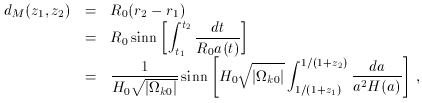
(|k0|)),
H(a) is again given by (30),
and ``sinn(x)'' denotes sinh(x) when
k0 < 0,
sin(x)
when k0 > 0, and
x when k0 = 0.
An analytic approximation formula can be found in [24].
Note that, for large redshifts, the dependence of the various
distance measures on z is not necessarily monotonic.
