3.4 Gravitational lensing

The volume of space back to a specified redshift, given by (44), depends sensitively on . Consequently, counting the apparent density of observed objects, whose actual density per cubic Mpc is assumed to be known, provides a potential test for the cosmological constant [112, 113, 114, 3] Like tests of distance vs. redshift, a significant problem for such methods is the luminosity evolution of whatever objects one might attempt to count. A modern attempt to circumvent this difficulty is to use the statistics of gravitational lensing of distant galaxies; the hope is that the number of condensed objects which can act as lenses is less sensitive to evolution than the number of visible objects.

In a spatially flat universe, the probability of a source at redshift z_s being lensed, relative to the fiducial (_M = 1, = 0) case, is given by

(53)

where a_s = 1 / (1 + z_s).

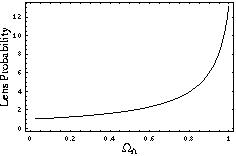
Figure 9. Gravitational lens probabilities in a flat universe with M + = 1, relative to M = 1, = 0, for a source at z = 2.

As shown in Figure (9), the probability rises dramatically as is increased to unity as we keep fixed. Thus, the absence of a large number of such lenses would imply an upper limit on .

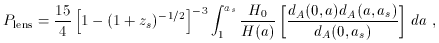
Analysis of lensing statistics is complicated by uncertainties in evolution, extinction, and biases in the lens discovery procedure. It has been argued [115, 116] that the existing data allow us to place an upper limit of < 0.7 in a flat universe. However, other groups [117, 118] have claimed that the current data actually favor a nonzero cosmological constant. The near future will bring larger, more objective surveys, which should allow these ambiguities to be resolved. Other manifestations of lensing can also be used to constrain , including statistics of giant arcs [119], deep weak-lensing surveys [120], and lensing in the Hubble Deep Field [121].