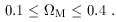3.3 Matter density
Many cosmological tests, such as the two just discussed, will
constrain some combination of
 M and
M and

 .
It is therefore useful to consider tests of
.
It is therefore useful to consider tests of
 M alone,
even if our primary goal is to determine
M alone,
even if our primary goal is to determine

 .
(In truth, it is also hard to constrain
.
(In truth, it is also hard to constrain
 M alone,
as almost all methods actually constrain some combination
of
M alone,
as almost all methods actually constrain some combination
of  M and the Hubble
constant h = H0
/ (100 km/sec/Mpc); the HST Key Project on the extragalactic
distance scale finds h = 0.71 ± 0.06
[86],
which is consistent with other methods
[87], and what
I will assume below.)
M and the Hubble
constant h = H0
/ (100 km/sec/Mpc); the HST Key Project on the extragalactic
distance scale finds h = 0.71 ± 0.06
[86],
which is consistent with other methods
[87], and what
I will assume below.)
For years, determinations of
 M based on dynamics
of galaxies and clusters have yielded values between approximately
0.1 and 0.4 - noticeably larger than the density parameter in
baryons as inferred from primordial nucleosynthesis,
M based on dynamics
of galaxies and clusters have yielded values between approximately
0.1 and 0.4 - noticeably larger than the density parameter in
baryons as inferred from primordial nucleosynthesis,
 B =
(0.019 ± 0.001) h-2
B =
(0.019 ± 0.001) h-2
 0.04
[88,
89],
but noticeably smaller than the critical density.
The last several years have witnessed a number of new methods
being brought to bear on the question; the quantitative results
have remained unchanged, but our confidence in them has increased
greatly.
0.04
[88,
89],
but noticeably smaller than the critical density.
The last several years have witnessed a number of new methods
being brought to bear on the question; the quantitative results
have remained unchanged, but our confidence in them has increased
greatly.
A thorough discussion of determinations of
 M
requires a review all its own, and good ones are available
[90,
91,
92,
87,
93].
Here I will just sketch some of the important methods.
M
requires a review all its own, and good ones are available
[90,
91,
92,
87,
93].
Here I will just sketch some of the important methods.
The traditional method to estimate
the mass density of the universe is to ``weigh'' a cluster of
galaxies, divide by its luminosity, and extrapolate the
result to the universe as a whole. Although clusters are not
representative samples of the universe, they are sufficiently
large that such a procedure has a chance of working. Studies
applying the virial theorem to cluster dynamics have typically
obtained values
 M = 0.2 ± 0.1
[94,
90,
91].
Although it is possible that
the global value of M/L differs appreciably from its value
in clusters, extrapolations from small scales do not seem
to reach the critical densit
[95]. New
techniques to weigh the clusters, including gravitational
lensing of background galaxies
[96] and
temperature profiles of the X-ray gas
[97], while not yet in
perfect agreement with each other, reach essentially
similar conclusions.
M = 0.2 ± 0.1
[94,
90,
91].
Although it is possible that
the global value of M/L differs appreciably from its value
in clusters, extrapolations from small scales do not seem
to reach the critical densit
[95]. New
techniques to weigh the clusters, including gravitational
lensing of background galaxies
[96] and
temperature profiles of the X-ray gas
[97], while not yet in
perfect agreement with each other, reach essentially
similar conclusions.
Rather than measuring the mass relative to the luminosity
density, which may be different inside and outside clusters,
we can also measure it with respect to the baryon density
[98],
which is very likely to have the same value in clusters as
elsewhere in the universe, simply because there is no way
to segregate the baryons from the dark matter on such large
scales. Most of the baryonic mass is in the hot intracluster
gas [99],
and the fraction fgas
of total mass in this form can be measured either by
direct observation of X-rays from the gas
[100] or by
distortions
of the microwave background by scattering off hot electrons
(the Sunyaev-Zeldovich effect)
[101], typically
yielding 0.1  fgas
fgas
 0.2.
Since primordial nucleosynthesis provides a determination
of
0.2.
Since primordial nucleosynthesis provides a determination
of  B ~ 0.04, these
measurements imply
B ~ 0.04, these
measurements imply
consistent with the value determined from mass to light ratios.
Another handle on the density parameter in matter comes from
properties of clusters at high redshift. The very existence
of massive clusters has been used to argue in favor of
The story of large-scale motions is more ambiguous. The
peculiar velocities of galaxies are sensitive to the underlying
mass density, and thus to
Finally, the matter density parameter can be extracted from
measurements of the power spectrum of density fluctuations
(see for example
[106]).
As with the CMB, predicting
the power spectrum requires both an assumption of the correct
theory and a specification of a number of cosmological
parameters. In simple models (e.g., with only cold dark
matter and baryons, no massive neutrinos), the spectrum can be
fit (once the amplitude is normalized) by a single ``shape
parameter'', which is found to be equal to
Even without the supernova results, this determination in
concert with the CMB measurements favoring a flat universe
provide a strong case for a nonzero cosmological constant.
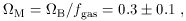
 M ~ 0.2
[102], and the
lack of appreciable
evolution of clusters from high redshifts to the present
[103,
104] provides
additional evidence that
M ~ 0.2
[102], and the
lack of appreciable
evolution of clusters from high redshifts to the present
[103,
104] provides
additional evidence that
 M < 1.0.
M < 1.0.
 M, but also to the
``bias'' describing the relative amplitude of fluctuations in
galaxies and mass
[90,
105]. Difficulties
both in measuring the flows and in disentangling the mass density
from other effects make it difficult to draw conclusions at
this point, and at present it is hard to say much more
than 0.2
M, but also to the
``bias'' describing the relative amplitude of fluctuations in
galaxies and mass
[90,
105]. Difficulties
both in measuring the flows and in disentangling the mass density
from other effects make it difficult to draw conclusions at
this point, and at present it is hard to say much more
than 0.2 
 M
M
 1.0.
1.0.
 =
=
 M h. (For
more complicated models see
[107].)
Observations then yield
M h. (For
more complicated models see
[107].)
Observations then yield
 ~ 0.25,
or
~ 0.25,
or  M ~ 0.36. For a
more careful comparison
between models and observations, see
[108,
109,
110,
111].
Thus, we have a remarkable convergence on values for the
density parameter in matter:
M ~ 0.36. For a
more careful comparison
between models and observations, see
[108,
109,
110,
111].
Thus, we have a remarkable convergence on values for the
density parameter in matter: