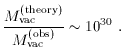In Section (1.3) we discussed the large
difference between the magnitude of the
vacuum energy expected from zero-point
fluctuations and scalar potentials, 
theor
~ 2 x 10110 erg/cm3,
and the value we apparently observe,
(obs) ~ 2 x
10-10 erg/cm3
(which may be thought of as an upper limit, if we wish
to be careful). It is somewhat unfair to characterize this
discrepancy as a factor of 10120, since energy density
can be expressed as a mass scale to the fourth power.
Writing =
Mvac4,
we find Mvac(theory) ~ MPl
~ 1018 GeV and
Mvac(obs) ~ 10-3 eV, so a more fair
characterization of the problem would be
Of course, thirty orders of magnitude still constitutes a
difference worthy of our attention.
Although the mechanism which suppresses the naive value
of the vacuum energy is unknown, it seems easier to imagine
a hypothetical scenario which makes it exactly zero than
one which sets it to just the right value to be observable
today. (Keeping in mind that it is the zero-temperature,
late-time
vacuum energy which we want to be small; it is expected to
change at phase transitions, and a large value in the early
universe is a necessary component of inflationary universe
scenarios
[21,
22,
23].
If the recent observations pointing toward a cosmological constant
of astrophysically relevant magnitude are confirmed, we will
be faced with the challenge of explaining not only why the
vacuum energy is smaller than expected, but also why it has
the specific nonzero value it does.
