


4.5 Other sources of dark energy
Although a cosmological constant is an excellent fit to the
current data, the observations can also be accommodated by
any form of ``dark energy'' which does not cluster
on small scales (so as to avoid being detected by measurements
of  M) and redshifts
away only very slowly as the
universe expands [to account for the accelerated expansion,
as per equation (32)]. This possibility has been
extensively explored of late, and a number of candidates
have been put forward.
M) and redshifts
away only very slowly as the
universe expands [to account for the accelerated expansion,
as per equation (32)]. This possibility has been
extensively explored of late, and a number of candidates
have been put forward.
One way to parameterize such a component X is by an effective
equation of state, pX = wX
 X.
(A large number of phenomenological models of this type have
been investigated, starting with the early work in
[206,
207];
see
[208,
8]
for many more references.) The relevant range for
wX is between 0 (ordinary matter) and -1 (true cosmological
constant); sources with wX > 0 redshift away more rapidly
than ordinary matter (and therefore cause extra deceleration),
while wX < -1 is unphysical by the criteria discussed in
Section 2.1 (although see
[209]).
While not every source
will obey an equation of state with wX = constant, it is
often the case that a single effective wX characterizes
the behavior for the redshift range over which the component
can potentially be observed.
X.
(A large number of phenomenological models of this type have
been investigated, starting with the early work in
[206,
207];
see
[208,
8]
for many more references.) The relevant range for
wX is between 0 (ordinary matter) and -1 (true cosmological
constant); sources with wX > 0 redshift away more rapidly
than ordinary matter (and therefore cause extra deceleration),
while wX < -1 is unphysical by the criteria discussed in
Section 2.1 (although see
[209]).
While not every source
will obey an equation of state with wX = constant, it is
often the case that a single effective wX characterizes
the behavior for the redshift range over which the component
can potentially be observed.
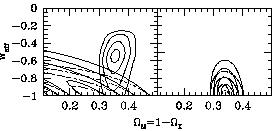
|
Figure 10. Limits from supernovae and
large-scale structure
data on |
Current observations of supernovae, large-scale structure,
gravitational lensing, and the CMB already
provide interesting limits on wX
[210,
211,
212,
213,
214,
49,
52,
215,
216,
217,
218,
219],
and future data will be able to do much better
[218,
220,
221,
222].
Figure (10) shows an example, in this case limits
from supernovae and large-scale structure
on wX and
 M in a universe which is
assumed to be flat and dominated by X and ordinary
matter. It is clear that the favored value for the
equation-of-state parameter is near -1, that of a true cosmological
constant, although other values are not completely ruled out.
M in a universe which is
assumed to be flat and dominated by X and ordinary
matter. It is clear that the favored value for the
equation-of-state parameter is near -1, that of a true cosmological
constant, although other values are not completely ruled out.
The simplest physical model for an appropriate dark
energy component is a single slowly-rolling scalar field,
sometimes referred to as ``quintessence''
[223,
224,
225,
226,
227,
228,
229,
230,
231,
232,
233,
234].
In an expanding universe, a spatially homogeneous scalar with potential
V( ) and minimal coupling to
gravity obeys
) and minimal coupling to
gravity obeys
where H is the Hubble parameter, overdots indicate time
derivatives, and primes indicate derivatives with respect to
which will generally vary with time. Thus, when the field
is slowly-varying and
There are many reasons to consider dynamical dark energy
as an alternative to a cosmological constant. First and foremost,
it is a logical possibility which might be correct, and can
be constrained by observation. Secondly, it is consistent with
the hope that the ultimate vacuum energy might actually be zero, and
that we simply haven't relaxed all the way to the vacuum as yet.
But most interestingly, one might wonder whether replacing a constant
parameter
Quintessence models also introduce new naturalness problems
in addition to those of a cosmological constant. These can be
traced to the fact that, in order for the field to be slowly-rolling
today, we require
sqrt[V''(
By particle-physics standards, this is an incredibly small
number; masses of scalar fields tend to be large in the
absence of a symmetry to protect them. Scalars of such a low
mass give rise to long-range forces if they couple to ordinary
matter; since
Nevertheless, these naturalness arguments are by no means
airtight, and it is worth considering specific particle-physics
models for the quintessence field. In addition to the
pseudo-Goldstone boson models just mentioned, these include
models based on supersymmetric gauge theories
[250,
251],
supergravity
[252,
253],
small extra dimensions
[254,
255],
large extra dimensions
[256,
257],
and non-minimal couplings to the
curvature scalar
[258,
259,
260,
261,
262,
263,
264,
265,
266].
Finally, the possibility has been raised that the scalar field
responsible for driving inflation may also serve as quintessence
[267,
268,
269,
270],
although
this proposal has been criticized for producing unwanted relics
and isocurvature fluctuations
[271].
There are other models of dark energy besides those based
on nearly-massless scalar fields. One scenario is ``solid''
dark matter, typically based on networks of tangled cosmic
strings or domain walls
[272,
273,
274,
275].
Strings give an effective equation-of-state parameter
wstring = -1/3, and walls have wwall
= -2/3,
so walls are a better fit to the data at present. There is
also the idea of dark matter particles whose masses increase
as the universe expands, their energy thus redshifting away more
slowly than that of ordinary matter
[276,
277] (see also
[278]).
The cosmological consequences of this kind of
scenario turn out to be difficult to analyze analytically, and
work is still ongoing.
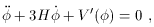
 . This equation is similar to (45),
with analogous solutions. The Hubble parameter acts as a
friction term; for generic potentials, the field will be
overdamped (and thus approximately constant) when
H > sqrt[V''(
. This equation is similar to (45),
with analogous solutions. The Hubble parameter acts as a
friction term; for generic potentials, the field will be
overdamped (and thus approximately constant) when
H > sqrt[V''( )], and
underdamped (and thus free to
roll) when H <
sqrt[V''(
)], and
underdamped (and thus free to
roll) when H <
sqrt[V''( )]. The energy density is
)]. The energy density is

 =
(1/2)
=
(1/2) 2 +
V(
2 +
V( ), and the
pressure is p
), and the
pressure is p = (1/2)
= (1/2)
 2 -
V(
2 -
V( ),
implying an equation of state parameter
),
implying an equation of state parameter
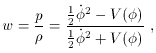
 2
<< V(
2
<< V( ), we have
w ~ -1, and the scalar field potential acts like a
cosmological constant.
), we have
w ~ -1, and the scalar field potential acts like a
cosmological constant.
 with a dynamical
field could allow us to
relieve some of the burden of fine-tuning that inevitably
accompanies the cosmological constant. To date, investigations
have focused on scaling or tracker models of quintessence, in
which the scalar field energy density can parallel that of matter
or radiation, at least for part of its history
[232,
235,
236,
237,
238,
239,
240].
(Of course, we do not want the
dark energy density to redshift away as rapidly as that in matter
during the current epoch, or the universe would not be accelerating.)
Tracker models can be constructed in which the vacuum energy
density at late times is robust, in the sense that it does not
depend sensitively on the initial conditions for the field.
However, the ultimate value
with a dynamical
field could allow us to
relieve some of the burden of fine-tuning that inevitably
accompanies the cosmological constant. To date, investigations
have focused on scaling or tracker models of quintessence, in
which the scalar field energy density can parallel that of matter
or radiation, at least for part of its history
[232,
235,
236,
237,
238,
239,
240].
(Of course, we do not want the
dark energy density to redshift away as rapidly as that in matter
during the current epoch, or the universe would not be accelerating.)
Tracker models can be constructed in which the vacuum energy
density at late times is robust, in the sense that it does not
depend sensitively on the initial conditions for the field.
However, the ultimate value
 vac ~
(10-3
eV)4 still depends sensitively on the parameters in
the potential. Indeed, it is hard to imagine how this could
help but be the case; unlike the case of the axion solution
to the strong-CP problem, we have no symmetry to appeal to that
would enforce a small vacuum energy, much less a particular
small nonzero number.
vac ~
(10-3
eV)4 still depends sensitively on the parameters in
the potential. Indeed, it is hard to imagine how this could
help but be the case; unlike the case of the axion solution
to the strong-CP problem, we have no symmetry to appeal to that
would enforce a small vacuum energy, much less a particular
small nonzero number.
 0)] ~
H0; but this
expression is the effective mass of fluctuations in
0)] ~
H0; but this
expression is the effective mass of fluctuations in
 , so we have
, so we have
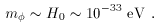
 does couple to
gravity, we expect at the
very least to have non-renormalizable interactions suppressed
by powers of the Planck scale. Such interactions are potentially
observable, both via fifth-force experiments and searches for
time-dependence of the constants of nature, and current limits
imply that there must be suppression of the quintessence couplings
by several orders of magnitude over what would be expected
[241,
242,
243].
The only known way to obtain such a suppression
is through the imposition of an approximate global symmetry
(which would also help explain the low mass of the field), of
the type characteristic of pseudo-Goldstone boson models of
quintessence, which have been actively explored
[230,
231,
244,
245,
246,
247].
(Cosmological pseudo-Goldstone bosons are
potentially detectable through their tendency to rotate polarized
radiation from galaxies and the CMB
[241,
248].
See [249]
for a discussion of further fine-tuning
problems in the context of supersymmetric models.
does couple to
gravity, we expect at the
very least to have non-renormalizable interactions suppressed
by powers of the Planck scale. Such interactions are potentially
observable, both via fifth-force experiments and searches for
time-dependence of the constants of nature, and current limits
imply that there must be suppression of the quintessence couplings
by several orders of magnitude over what would be expected
[241,
242,
243].
The only known way to obtain such a suppression
is through the imposition of an approximate global symmetry
(which would also help explain the low mass of the field), of
the type characteristic of pseudo-Goldstone boson models of
quintessence, which have been actively explored
[230,
231,
244,
245,
246,
247].
(Cosmological pseudo-Goldstone bosons are
potentially detectable through their tendency to rotate polarized
radiation from galaxies and the CMB
[241,
248].
See [249]
for a discussion of further fine-tuning
problems in the context of supersymmetric models.