


From the Friedmann equation
(5) (where henceforth we take the effects of a
cosmological constant into account by including the vacuum energy
density 
 into the total density
into the total density  ), for any
value of the Hubble parameter H there is a critical value
of the energy density such that the spatial geometry is flat
(k = 0):
), for any
value of the Hubble parameter H there is a critical value
of the energy density such that the spatial geometry is flat
(k = 0):
It is often most convenient to measure the total energy
density in terms of the critical density, by introducing the
density parameter
One useful feature of this parameterization is a direct
connection between the value of
[Keep in mind that some references still use
``
In general, the energy density
with wi a constant. Plugging this equation of state into
the energy-momentum conservation equation
where the exponent is related to the equation of state parameter by
The density parameter in each component is defined in the
obvious way,
which has the useful property that
The simplest example of a component of this form is a set
of massive particles with negligible relative velocities,
known in cosmology as ``dust'' or simply ``matter''.
The energy density of such particles is given by their
number density times their rest mass; as the universe
expands, the number density is inversely proportional to the
volume while the rest masses are constant, yielding
this relation is simply (5) divided by H2. Note that the
contribution from
where the notation
The ranges of values of the
There are good reasons to believe that the energy density in
radiation today is much less than that in matter. Photons,
which are readily detectable, contribute
One way to characterize a specific
Friedmann-Robertson-Walker model is by the values of
the Hubble parameter and the various energy densities
where in the last line we have assumed that the universe is
dominated by matter and the cosmological constant.
Under the assumption that
Notice that
positive-energy-density sources with n > 2 cause the universe to
decelerate while n < 2 leads to acceleration; the more rapidly
energy density redshifts away, the greater the tendency towards
universal deceleration. An empty universe
(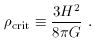
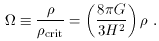
 and the spatial
geometry:
and the spatial
geometry:
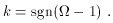
 ''
to refer strictly to the density parameter in matter, even
in the presence of a cosmological constant; with this
definition (23) no longer holds.]
''
to refer strictly to the density parameter in matter, even
in the presence of a cosmological constant; with this
definition (23) no longer holds.]
 will include
contributions from various distinct components.
From the point of view of cosmology, the relevant feature of
each component is how its energy density evolves as the universe
expands. Fortunately, it is often (although not always) the
case that individual components i have very simple equations
of state of the form
will include
contributions from various distinct components.
From the point of view of cosmology, the relevant feature of
each component is how its energy density evolves as the universe
expands. Fortunately, it is often (although not always) the
case that individual components i have very simple equations
of state of the form
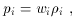
 µ
Tµ
µ
Tµ = 0, we find that the energy density has a power-law dependence
on the scale factor,
= 0, we find that the energy density has a power-law dependence
on the scale factor,
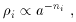
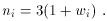
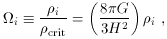
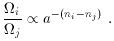
 M
M
 a-3. For
relativistic particles,
known in cosmology as ``radiation'' (although any relativistic
species counts, not only photons or even strictly massless
particles), the energy density is the number density times
the particle energy, and the latter is proportional to a-1
(redshifting as the universe expands); the radiation energy
density therefore scales as
a-3. For
relativistic particles,
known in cosmology as ``radiation'' (although any relativistic
species counts, not only photons or even strictly massless
particles), the energy density is the number density times
the particle energy, and the latter is proportional to a-1
(redshifting as the universe expands); the radiation energy
density therefore scales as
 R
R
 a-4.
Vacuum energy does not change as the universe expands, so
a-4.
Vacuum energy does not change as the universe expands, so


 a0;
from (26) this implies a
negative pressure, or positive tension, when the vacuum energy is
positive. Finally, for some purposes it is
useful to pretend that the -ka-2
R0-2 term in (5)
represents an effective ``energy density in curvature'',
and define
a0;
from (26) this implies a
negative pressure, or positive tension, when the vacuum energy is
positive. Finally, for some purposes it is
useful to pretend that the -ka-2
R0-2 term in (5)
represents an effective ``energy density in curvature'',
and define  _k
_k
 -(3k /
8
-(3k /
8 GR02) a-2. We can define a
corresponding density parameter
GR02) a-2. We can define a
corresponding density parameter
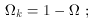
 k
is (for obvious reasons) not included in the definition of
k
is (for obvious reasons) not included in the definition of
 . The usefulness of
. The usefulness of
 k is that it
contributes to the expansion rate
analogously to the honest density parameters
k is that it
contributes to the expansion rate
analogously to the honest density parameters
 i; we can write
i; we can write

 i(k)
reflects the fact that the
sum includes
i(k)
reflects the fact that the
sum includes  k in
addition to the various components
of
k in
addition to the various components
of  =
=
 i
i
 i. The most popular
equations of
state for cosmological energy sources can thus be summarized
as follows:
i. The most popular
equations of
state for cosmological energy sources can thus be summarized
as follows:
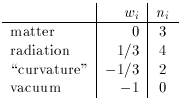
 i's which are allowed in
principle (as opposed to constrained by observation) will depend
on a complete theory of the matter fields, but lacking that we
may still invoke energy conditions to get a handle on what
constitutes sensible values. The most appropriate condition
is the dominant energy condition (DEC), which
states that Tµ
i's which are allowed in
principle (as opposed to constrained by observation) will depend
on a complete theory of the matter fields, but lacking that we
may still invoke energy conditions to get a handle on what
constitutes sensible values. The most appropriate condition
is the dominant energy condition (DEC), which
states that Tµ lµ
l
lµ
l
 0, and
Tµ
0, and
Tµ lµ is non-spacelike, for any
null vector lµ; this implies that energy does not
flow faster than the speed of light
[17].
For a perfect-fluid energy-momentum
tensor of the form (4), these two requirements
imply that
lµ is non-spacelike, for any
null vector lµ; this implies that energy does not
flow faster than the speed of light
[17].
For a perfect-fluid energy-momentum
tensor of the form (4), these two requirements
imply that  +
p
+
p  0 and
|
0 and
| |
|
 |p|, respectively.
Thus, either the density is positive and greater in magnitude
than the pressure, or the density is negative and equal in
magnitude to a compensating positive pressure; in terms of the
equation-of-state parameter w, we have either positive
|p|, respectively.
Thus, either the density is positive and greater in magnitude
than the pressure, or the density is negative and equal in
magnitude to a compensating positive pressure; in terms of the
equation-of-state parameter w, we have either positive
 and |w|
and |w|
 1 or negative
1 or negative  and
w = -1. That is,
a negative energy density is allowed only if it is in the form
of vacuum energy. (We have actually modified the conventional
DEC somewhat, by using only null vectors lµ rather than
null or timelike vectors; the traditional condition would
rule out a negative cosmological constant, which there is no
physical reason to do.)
and
w = -1. That is,
a negative energy density is allowed only if it is in the form
of vacuum energy. (We have actually modified the conventional
DEC somewhat, by using only null vectors lµ rather than
null or timelike vectors; the traditional condition would
rule out a negative cosmological constant, which there is no
physical reason to do.)

 ~ 5 x 10-5, mostly in the
2.73 °K cosmic microwave background
[18,
19,
20].
If neutrinos are sufficiently low mass as to
be relativistic today, conventional
scenarios predict that they contribute approximately the same
amount [11].
In the absence of sources which are even more exotic,
it is therefore useful to parameterize the universe today by
the values of
~ 5 x 10-5, mostly in the
2.73 °K cosmic microwave background
[18,
19,
20].
If neutrinos are sufficiently low mass as to
be relativistic today, conventional
scenarios predict that they contribute approximately the same
amount [11].
In the absence of sources which are even more exotic,
it is therefore useful to parameterize the universe today by
the values of  M and
M and

 , with
, with
 k = 1 -
k = 1 -
 M -
M -

 , keeping
the possibility of surprises always in mind.
, keeping
the possibility of surprises always in mind.
 i. (Of
course, reconstructing the history of such a
universe also requires an understanding of the microphysical
processes which can exchange energy between the different
states.) It may be difficult, however, to directly measure the
different contributions to
i. (Of
course, reconstructing the history of such a
universe also requires an understanding of the microphysical
processes which can exchange energy between the different
states.) It may be difficult, however, to directly measure the
different contributions to
 , and it is therefore useful
to consider extracting these quantities from the behavior of
the scale factor as a function of time. A traditional measure
of the evolution of the expansion rate is the deceleration
parameter
, and it is therefore useful
to consider extracting these quantities from the behavior of
the scale factor as a function of time. A traditional measure
of the evolution of the expansion rate is the deceleration
parameter
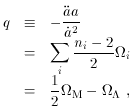

 = 0,
measuring
q0 provides a direct measurement of the current density
parameter
= 0,
measuring
q0 provides a direct measurement of the current density
parameter  M0; however, once
M0; however, once

 is admitted as a possibility there is no single parameter
which characterizes various universes, and for most purposes
it is more convenient to simply quote experimental results
directly in terms of
is admitted as a possibility there is no single parameter
which characterizes various universes, and for most purposes
it is more convenient to simply quote experimental results
directly in terms of  M and
M and

 .
[Even this parameterization, of course, bears a certain theoretical
bias which may not be justified; ultimately, the only unbiased
method is to directly quote limits on a(t).]
.
[Even this parameterization, of course, bears a certain theoretical
bias which may not be justified; ultimately, the only unbiased
method is to directly quote limits on a(t).]
 = 0,
= 0,
 k = 1)
expands linearly with time; sometimes called the ``Milne
universe'', such a spacetime is really flat Minkowski space
in an unusual time-slicing.
k = 1)
expands linearly with time; sometimes called the ``Milne
universe'', such a spacetime is really flat Minkowski space
in an unusual time-slicing.