


A point of some confusion which needs clarification when discussing Cepheids as distance indicators resides in the difference between the PLC and the PL relation. As discussed earlier, the PLC is simply a restatement of Stefan's Law, and it is therefore applicable to all stars on an individual basis. The PL and PC relations, on the other hand, are statistical relations for ensembles of stars; and they are in turn the result of constraints on Stefan's Law. That constraint is manifest in nature as a strip in which stars are unstable to pulsation. Here we expand on and illustrate this statement of differences.
A PLC relation exists for all stars. That is, for all combinations of temperature and luminosity one can calculate a period, since the PLC embodies exactly the same (universally applicable) principles as does Stephan's Law, from which it is derived. To use the PLC formalization, one must of course observe a color, correct it to an intrinsic color, and then independently determine a fundamental period in order to calculate a luminosity. But while all stars may have mathematically and physically well-defined fundamental-mode periods, not all stars are unstable to these oscillations, and so their pulsational periods often are not manifested directly.
Much as Nature has provided us with a useful and powerful constraint on Stephan's Law, through the hydrogen burning main sequence, Nature has also provided a different constraint on Stephan's Law (i.e., a constraint on the ubiquitous PLC relation) by defining a narrow zone in which stable pulsation can and does occur. This alternate ``constraint'' manifests itself as the Cepheid instability strip. The Cepheid instability strip itself, should not be confused with the period-luminosity-color relation. The Cepheid instability strip defines a range of luminosities, colors, and periods over which pulsation is a stable mode for the star and is therefore an observable. But this constraint does not control the detailed correlations between period, temperature and luminosity, nor does it control the interdependence of the observed parameters for individual stars. In much the same way, the main sequence is a strip of stable hydrogen burning, where stars are constrained to spend a large fraction of their luminous lifetimes. While the gross details of the main sequence are controlled by a single parameter (the mass of the star) the individual stars in this narrowly defined range (the main sequence) still obey the two-parameter Stephan's Law.
The Cepheid constraint, in the form of an instability strip, controls the statistical properties of the ensemble of Cepheid variable stars. As such, physical laws external to Stephan's Law are responsible for the now famous group statistical trends of the period-luminosity and period-color relations. But these trends are incomplete (and even sometimes misleading) descriptors for individual stars: that is to say the properties of individual stars can never be accurately defined by the constraints on the PLC relation, but only by the PLC relation itself.
To illustrate how fundamentally different these two concepts (of the underlying equations and the overlaying constraints) are, the interested reader is referred to an earlier paper on the subject (Madore & Freedman 1991). However, the flavor of the argument can be had from considering Figure 8. The solid slanting lines in each figure represent the lines of constant period for the same underlying PLC relation. The heavy pair of lines cutting the constant-period lines represent two extreme examples of hypothetical boundaries to the instability strip inside of which stars are allowed to pulsate. If we now project each of these diagrams into alternate representations of the data, using the period as the abscissa, we get the corresponding period-luminosity and period-color relations as given in Figure 9 and 10. In the period-luminosity representation of the data contained in Figure 9, (where the instability strip is essentially vertical in the CM diagram), there is a strong statistical trend of luminosity with period. However, in the corresponding period-color plot (Figure 10), there is no correlation at all, in a statistical sense; yet for individual stars the period, luminosity and color are in any case perfectly correlated through the period-luminosity-color relation. Conversely, in Figure 9, there is no statistical Period-Luminosity relation; there is a very strong Period-Color relation, and yet again precisely the same PLC relation is generating the data. Only the constraints have changed.
 Figure 8. Projections of the Instability
Strip. The Cepheid instability strip is shown plotted in the upper left-hand
panel. Lines of constant period (P1,
P2, P3, etc.) are shown as
thick lines crossing between the red and blue edges of the instability
strip, which act as constraints on the underlying PLC relation which
would otherwise fill the plane, as in
Figure 3. The broken horizontal
lines show how the instability strip and the lines of constant period
map over into the period-luminosity plane, while the vertical lines
show the mapping down into the period-color plane (which can be viewed
in its normal orientation by rotating the diagram 90 degrees
counterclockwise.
Figure 8. Projections of the Instability
Strip. The Cepheid instability strip is shown plotted in the upper left-hand
panel. Lines of constant period (P1,
P2, P3, etc.) are shown as
thick lines crossing between the red and blue edges of the instability
strip, which act as constraints on the underlying PLC relation which
would otherwise fill the plane, as in
Figure 3. The broken horizontal
lines show how the instability strip and the lines of constant period
map over into the period-luminosity plane, while the vertical lines
show the mapping down into the period-color plane (which can be viewed
in its normal orientation by rotating the diagram 90 degrees
counterclockwise.
The distribution of observed data points (drawn from the underlying PLC) may be constrained both by observational selection effects and/or by different physics, without necessarily violating the two-parameter period-luminosity-color relation. Accordingly, differences in the statistical correlations (PL, PC, etc.) do not, of necessity, signal deeper-seated differences in the properties of the individual stars. On the other hand, differences in the bulk properties of an ensemble may be taken as fair warning that the detailed physics is changing too. In fact, it is difficult to understand why and how the two properties could be decoupled.
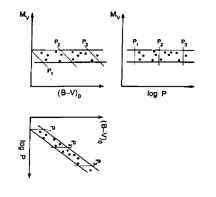 Figure 9. The same as
Figure 8 except now
a different instability strip is imposed on the underlying universal
PLC. This instability strip is horizontal in the CM diagram resulting in a
definite statistical correlation of color with period (lower panel,
rotated by 90 degrees), but no trend of luminosity with period
(right-hand panel).
Figure 9. The same as
Figure 8 except now
a different instability strip is imposed on the underlying universal
PLC. This instability strip is horizontal in the CM diagram resulting in a
definite statistical correlation of color with period (lower panel,
rotated by 90 degrees), but no trend of luminosity with period
(right-hand panel).
It is, of course, historically very important that the instability strip is naturally oriented in such a way as to give not only a statistical PL, but also a statistical PC relation, for it was in attempts to utilize both of these relations (and to understand the ``scatter'' about their means) that ultimately led to the empirical formulation of a PLC (Sandage 1958).
 Figure 10. The same as
Figure 8 except
now a second instability strip is imposed on the underlying universal
PLC. This instability strip is vertical in the CM diagram resulting in a
definite statistical correlation of luminosity with period (right-hand
panel), but showing no trend of color with period (lower panel,
rotated by 90 degrees).
Figure 10. The same as
Figure 8 except
now a second instability strip is imposed on the underlying universal
PLC. This instability strip is vertical in the CM diagram resulting in a
definite statistical correlation of luminosity with period (right-hand
panel), but showing no trend of color with period (lower panel,
rotated by 90 degrees).