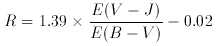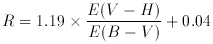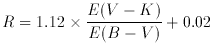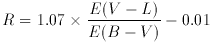The Full R-Dependent Curve
Figure 7 shows the full wavelength range of the
IR-through-UV
R-dependent extinction curves derived here, for four representative
values of R (thick solid and dashed lines). For 
 2700
Å the curves are computed using the FM fitting function and for
2700
Å the curves are computed using the FM fitting function and for
 > 2700 Å the curves are
spline interpolations
between the R-dependent spline anchors. The CCM results are shown
for comparison by the thin dotted lines for the same four R values.
In the UV region, the new results and the CCM curves are similar for R
> 2700 Å the curves are
spline interpolations
between the R-dependent spline anchors. The CCM results are shown
for comparison by the thin dotted lines for the same four R values.
In the UV region, the new results and the CCM curves are similar for R
 ~4.0, but diverge for larger
R. The main reason for this
discrepancy lies in the UV linear extinction component. While CCM
adopted a linear relationship between the slope c2 and intercept
c1, their relation - shown by the dotted line in the bottom panel
of Figure 5 - does not agree
well with the observations. The large
discrepancy at small values of c2 (i.e., large R) produces the
difference seen in Figure 7.
~4.0, but diverge for larger
R. The main reason for this
discrepancy lies in the UV linear extinction component. While CCM
adopted a linear relationship between the slope c2 and intercept
c1, their relation - shown by the dotted line in the bottom panel
of Figure 5 - does not agree
well with the observations. The large
discrepancy at small values of c2 (i.e., large R) produces the
difference seen in Figure 7.
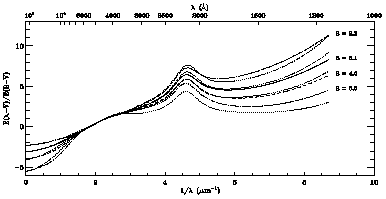
|
Figure 7. Examples of the
R-dependent far-IR through UV extinction
curves derived in this paper (thick solid and dashed curves). The
corresponding values of R are listed on the righthand side of the
figure beside the curves. For comparison, the results of CCM for the
same four values of R are shown.
|
A closeup comparison between the new results and CCM in the optical/IR
region for the R = 3.1 case can be seen in
Figure 6, where the CCM
curve is indicated by the dotted line. The disagreement in the region
near the Johnson R filter illustrates the bandwidth effect discussed
above. The CCM curve is fixed at A( ) / E (B - V) = 2.32 at 7000
Å, which is taken as
) / E (B - V) = 2.32 at 7000
Å, which is taken as  eff for the Johnson R. The new
curve is constructed to yield the same value of A(
eff for the Johnson R. The new
curve is constructed to yield the same value of A( ) / E (B - V) but
for synthetic photometry with the Johnson R. The discrepancy is
particularly large for this filter because of the steep change in
extinction across its relatively broad profile. This effect also
accounts for the lesser discrepancies in the regions of the U, B,
I, and J filters.
O'Donnell (1994)
presented a revision to
the CCM formula in the region of the U, B, and V
filters based on the
Strömgren photometric indices. This revision uses the same stategy
as CCM of fixing the extinction ratios at the filter effective
wavelengths, but more closely resembles the newly derived monochromatic
extinction curve because the bandwidth effects in the narrower
Strömgren filters are smaller.
) / E (B - V) but
for synthetic photometry with the Johnson R. The discrepancy is
particularly large for this filter because of the steep change in
extinction across its relatively broad profile. This effect also
accounts for the lesser discrepancies in the regions of the U, B,
I, and J filters.
O'Donnell (1994)
presented a revision to
the CCM formula in the region of the U, B, and V
filters based on the
Strömgren photometric indices. This revision uses the same stategy
as CCM of fixing the extinction ratios at the filter effective
wavelengths, but more closely resembles the newly derived monochromatic
extinction curve because the bandwidth effects in the narrower
Strömgren filters are smaller.
Note that the technique used here to produce R-dependent curves can
be used to construct ``customized'' UV/optical extinction curves for
sightlines with well-defined UV extinction properties. It is simply
necessary to substitute the measured values of A( ) / E (B - V) at
2700 Å and 2600 Å for the UV spline anchors listed in
Table 3
and then perform the cubic spline interpolation to determine the
optical portion of the curve, which smoothly joins the measured UV
curve at 2700 Å. This method was used in
Figure 2 to extend the
IUE curves into the optical region.
) / E (B - V) at
2700 Å and 2600 Å for the UV spline anchors listed in
Table 3
and then perform the cubic spline interpolation to determine the
optical portion of the curve, which smoothly joins the measured UV
curve at 2700 Å. This method was used in
Figure 2 to extend the
IUE curves into the optical region.
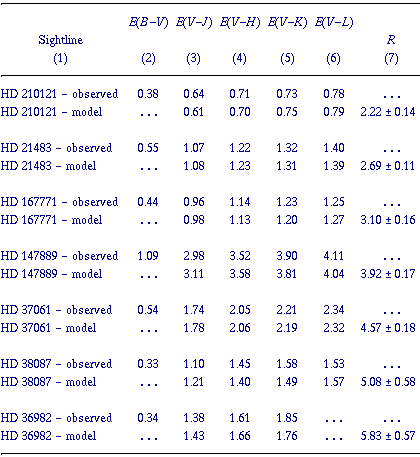
The assertion that the shape of the IR extinction law is invariant can
be tested by comparing results obtained from the R-dependent curves
in Figure 7 - which were constructed based on
this assumption - with observations. This comparison is made in
Table 5 for a number of
sightlines which span the observed range in R. The ``model'' data
listed for each sightline are the results from synthetic photometry on
model stellar energy distributions artificially reddened using the
R-dependent curves, with E (B - V) values from column 2 of
the table
and R values from column 7. The listed values of R are those that
best reproduce the observed color excesses and the uncertainties result
from assuming uncertainties of ±0.02 mag in E (B - V) and
±0.05 mag in the IR E (V- ). The agreement between observations and
model values is excellent and there are no strong systematic trends
evident. The results are thus consistent with an invariant IR
extinction curve. At wavelengths greater than ~ 1 µm, the
extinction curve roughly resembles a power law with an index of ~ 1.5.
This is similar to that adopted by CCM (1.6), but much flatter than
that of Martin & Whittet
(1990; ~ 1.8).
). The agreement between observations and
model values is excellent and there are no strong systematic trends
evident. The results are thus consistent with an invariant IR
extinction curve. At wavelengths greater than ~ 1 µm, the
extinction curve roughly resembles a power law with an index of ~ 1.5.
This is similar to that adopted by CCM (1.6), but much flatter than
that of Martin & Whittet
(1990; ~ 1.8).
Values of R are sometimes estimated from the relation R
 1.1 x E (V - K) / E (B -
V). Exact relationships between R and the IR color
excesses can be derived for the new R-dependent curves. These are
given by
1.1 x E (V - K) / E (B -
V). Exact relationships between R and the IR color
excesses can be derived for the new R-dependent curves. These are
given by
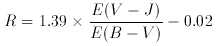 (A3)
(A3)
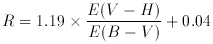 (A4)
(A4)
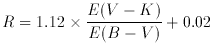 (A5)
(A5)
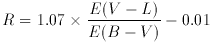 (A6)
(A6)
The coefficients in each of these equations actually depend on
the value of E (B - V) itself but, over the range E (B -
V) = 0-2.0,
vary by only several hundredths. The values in the equations are the
results for E (B - V) = 0.5.
At the blue end of the optical region, the interpolation between the
optical and UV spline anchor points can be tested by comparing
predictions of the extinction indices E (U - B) / E (B - V) and
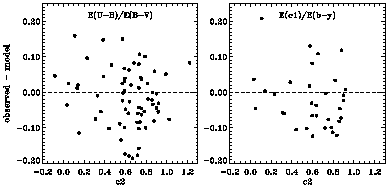
E (c1) / E (b - y) with photometric measurements.
Figure 8 shows this
comparison, with the difference between the observed values and
predicted values - derived from synthetic photometry of
``customized'' extinction curves from the FM sample - plotted against
the slope of the linear component c2. The curves were produced as
described above, by adopting the observed values of A( ) / E (B - V)
at 2600 Å and 2700 Å as the UV anchor points. The random scatter
(measurement noise) in both indices is large, but no
systematic trends are seen and the model curves appear to reproduce at
least the integrated properties of extinction well in the near-UV
region. Over the range of c2 values shown, the model values of
E (U - B) / E (B - V) range from about 0.6 to 0.8 and the values of
E (c1) / E (b - y) from about 0.0 to 0.3.
) / E (B - V)
at 2600 Å and 2700 Å as the UV anchor points. The random scatter
(measurement noise) in both indices is large, but no
systematic trends are seen and the model curves appear to reproduce at
least the integrated properties of extinction well in the near-UV
region. Over the range of c2 values shown, the model values of
E (U - B) / E (B - V) range from about 0.6 to 0.8 and the values of
E (c1) / E (b - y) from about 0.0 to 0.3.
|
Figure 8. Left Panel:
Observed-minus-predicted values of E (U - B) / E (B - V) plotted
against the slope of the UV linear extinction
component c2 (filled circles) for sightlnes from the FM sample.
Model values of E (U - B) / E (B - V) vary over the range ~ 0.6 to
~ 0.8 for the observed range in c2. Right Panel: Observed
minus predicted values of the Strömgren extinction ratio
E (c1) / E (b - y) plotted against c2 (filled
circles) for the FM sightlines with Strömgren data. Model values
of E (c1) / E (b - y)
vary over the range ~ 0.0 to ~ 0.3 for the observed range in c2.
|
In summary, the R-dependent curves derived here reproduce existing
photometric and spectrophotometric measurements and provide a good
estimate of the true monochromatic wavelength dependence of
interstellar extinction in the IR-through-UV regions. These curves
should be preferred for dereddening UV, optical, and near-IR
spectrophotometry. Since the new curves give the detailed wavelength
dependence of extinction, they can be used to predict the extinction
relationships for any photometric system by using synthetic photometry
of artificially reddened energy distributions. An IDL procedure to
produce the new curves at any desired value of R and over any
wavelength range can be obtained from the author or via anonymous ftp
at astro1.vill.edu. After logging in, change directories to
pub/fitz/Extinction, and download the file ``FMRCURVE.pro.''
Alternatively, this directory contains a series of compressed files
named ``FMRCURVEn.n.txt'' (e.g., ``FMRCURVE3.1.txt'') which contain
ASCII versions of the curves for various values of R (``n.n''). Two
columns of data are contained in each file; the first contains
wavelengths in Å and the second contains the extinction curve in
A( ) / E (B -
V). There are 1099 sets of points in each file.
) / E (B -
V). There are 1099 sets of points in each file.




 2700
Å the curves are computed using the FM fitting function and for
2700
Å the curves are computed using the FM fitting function and for
 > 2700 Å the curves are
spline interpolations
between the R-dependent spline anchors. The CCM results are shown
for comparison by the thin dotted lines for the same four R values.
In the UV region, the new results and the CCM curves are similar for R
> 2700 Å the curves are
spline interpolations
between the R-dependent spline anchors. The CCM results are shown
for comparison by the thin dotted lines for the same four R values.
In the UV region, the new results and the CCM curves are similar for R
 ~4.0, but diverge for larger
R. The main reason for this
discrepancy lies in the UV linear extinction component. While CCM
adopted a linear relationship between the slope c2 and intercept
c1, their relation - shown by the dotted line in the bottom panel
of Figure 5 - does not agree
well with the observations. The large
discrepancy at small values of c2 (i.e., large R) produces the
difference seen in Figure 7.
~4.0, but diverge for larger
R. The main reason for this
discrepancy lies in the UV linear extinction component. While CCM
adopted a linear relationship between the slope c2 and intercept
c1, their relation - shown by the dotted line in the bottom panel
of Figure 5 - does not agree
well with the observations. The large
discrepancy at small values of c2 (i.e., large R) produces the
difference seen in Figure 7.




 E(B-V) = 0.02 and
E(B-V) = 0.02 and  1.1 x E (V - K) / E (B -
V). Exact relationships between R and the IR color
excesses can be derived for the new R-dependent curves. These are
given by
1.1 x E (V - K) / E (B -
V). Exact relationships between R and the IR color
excesses can be derived for the new R-dependent curves. These are
given by