


4.2. Gravitational Lensing Frequencies for Quasars
The gravitational lensing optical depth is given by
where F = < 16
In order to acquire information for a smaller
There are continuous efforts
for nearly a decade that have brought substantial improvement in
reducing these uncertainties
(Maoz & Rix 1993;
Kochanek 1996;
Falco et al. 1998).
Nevertheless,
the issue (1) still remains as a cause of a large uncertainty.
While the total luminosity density is known to an uncertainty of 20% or so,
the fraction of early type galaxies is more uncertain.
It varies from 0.20 to 0.41 depending on the literature.
Including other items, it is likely that an estimate of F has a
50% uncertainty. For the curve in Figure 5 a
change of F by ± 50% brings the most likely value of
Kochanek and collaborators have made detailed
considerations on the above uncertainties, and
carried out elaborate statistical analyses.
In their latest publication they concluded
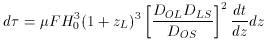
 3
ng
3
ng
 4g
H0-3 >, and µ is a
magnification factor. The cosmological factor
in (14) is very sensitive to the cosmological constant, when it dominates
(Fukugita & Turner
1991).
F is the astrophysical factor that depends on the galaxy number
density ng and the mass distribution of galaxies,
which is usually
assumed to be a singular isothermal sphere with velocity dispersion
4g
H0-3 >, and µ is a
magnification factor. The cosmological factor
in (14) is very sensitive to the cosmological constant, when it dominates
(Fukugita & Turner
1991).
F is the astrophysical factor that depends on the galaxy number
density ng and the mass distribution of galaxies,
which is usually
assumed to be a singular isothermal sphere with velocity dispersion
 g.
Figure 5 shows a typical
calculation for the expected number of strong lenses for 504 quasars
of the HST Snapshot Survey
(Maoz et al. 1993)
sample: the observed number is 5 (4 if 0957+561 is excluded).
The curve shows a high sensitivity to
g.
Figure 5 shows a typical
calculation for the expected number of strong lenses for 504 quasars
of the HST Snapshot Survey
(Maoz et al. 1993)
sample: the observed number is 5 (4 if 0957+561 is excluded).
The curve shows a high sensitivity to
 for
for
 > 0.7,
but in contrast a nearly flat dependence for a lower
> 0.7,
but in contrast a nearly flat dependence for a lower
 . It is
likely that
. It is
likely that  > 0.8 is
excluded. On the other hand, a more stringent limit is liable to be elusive.
Fifty percent uncertainty in the F factor,
say, would change largely a limit on, or a likely value of,
> 0.8 is
excluded. On the other hand, a more stringent limit is liable to be elusive.
Fifty percent uncertainty in the F factor,
say, would change largely a limit on, or a likely value of,
 .
.
 , an
accurate estimate is essential for the F factor, which receives
the following
uncertainties in: (1) the luminosity density and the fraction of early-type
galaxies (the lensing power of E and S0 galaxies is much higher than that
of spirals, and F is roughly proportional to the luminosity density of
early-type galaxies); (2)
, an
accurate estimate is essential for the F factor, which receives
the following
uncertainties in: (1) the luminosity density and the fraction of early-type
galaxies (the lensing power of E and S0 galaxies is much higher than that
of spirals, and F is roughly proportional to the luminosity density of
early-type galaxies); (2)
 g-luminosity relation
(Faber-Jackson relation); (3) the relation
between
g-luminosity relation
(Faber-Jackson relation); (3) the relation
between  (dark matter) and
(dark matter) and
 (star); (4) the model
profile of dark haloes, specifically the validity of the
singular isothermal sphere approximation (note that dark matter distributions
seem more complicated in elliptical galaxies than in spiral galaxies, see
Fukugita & Peebles
1999);
(5) the core radius which leads to a substantial reduction in
d
(star); (4) the model
profile of dark haloes, specifically the validity of the
singular isothermal sphere approximation (note that dark matter distributions
seem more complicated in elliptical galaxies than in spiral galaxies, see
Fukugita & Peebles
1999);
(5) the core radius which leads to a substantial reduction in
d ;
(6) selection effects of the observations; (7) dust obscuration; (8)
evolution of early-type galaxies.
;
(6) selection effects of the observations; (7) dust obscuration; (8)
evolution of early-type galaxies.
 to 0.75 or 0.2.
to 0.75 or 0.2.
 < 0.62 at 95% confidence
level from an optical sample
(Kochanek 1996).
They took the fraction
of early-type galaxies to be 0.44 and assigned a rather small
1
< 0.62 at 95% confidence
level from an optical sample
(Kochanek 1996).
They took the fraction
of early-type galaxies to be 0.44 and assigned a rather small
1 error. (The predicted frequency comes close to the upper envelope of
Fig. 5, and the observed number of lenses in the
HST sample is taken to be 4).
If one would adopt a smaller early-type fraction, the limit is
immediately loosened by a substantial amount.
Since the uncertainty is dominated by systematics rather than
statistical, it seems dangerous to give significance to statistics.
Statistical significance depends on artificial
elements as to what are assumed in the input.
A similar comment also applies to the recent work
claiming for a positive
error. (The predicted frequency comes close to the upper envelope of
Fig. 5, and the observed number of lenses in the
HST sample is taken to be 4).
If one would adopt a smaller early-type fraction, the limit is
immediately loosened by a substantial amount.
Since the uncertainty is dominated by systematics rather than
statistical, it seems dangerous to give significance to statistics.
Statistical significance depends on artificial
elements as to what are assumed in the input.
A similar comment also applies to the recent work
claiming for a positive  (Chiba & Yoshii
1997;
Cheng & Krauss
1998).
I would conclude a conservative limit being
(Chiba & Yoshii
1997;
Cheng & Krauss
1998).
I would conclude a conservative limit being
 < 0.8.
< 0.8.