4.3. Harmonics of CBR Anisotropies
so I will only briefly mention it for completeness.
The positions of the acoustic
peaks are particularly sensitive to
and
, and
even low accuracy data available at present lead to a meaningful
constraint on a combination of
and
.
The first acoustic peak appears at l =
(the distance
to the last-scattering surface)/(the sound horizon)
(Hu & Sugiyama 1995).
Its position l1 is approximated as
for the parameter range that concerns us.
This means that the position of the acoustic peak is about
l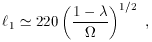 
220 if
+
= 1, but it
shifts to a high l as
-1/2 if
= 0.
On the other hand, there is little power to determine
separately from , unless full
information of Cl
is used.
The harmonics Cl measured at small angles revealed the
acoustic peak
(Scott et al. 1996),
and its position favours a universe not far from flat
(Hancock et
al. 1998).
More exhaustive analyses of
Lineweaver
(1998) and
Efstathiou et
al. (1999)
show a limit
+
/2 > 0.52
(1
). (The contours of the
confidence level
fall approximately on the curve given by (15) with l1
= constant.)
This means that a zero
universe is already marginal,
when combined with
from other arguments.
If a flat universe is chosen from CBR, a non-zero
will be compelling.