5. CONCLUSIONS

The status of and is summarised in TABLE 9. We have a reasonable convergence of the parameter towards a low value = 0.15-0.4. The convergence of is significantly better with the presence of the cosmological constant that makes the universe flat. Particularly encouraging is that the parameters derived with the aid of structure formation models agree with each other. This is taken to be an important test for the cosmological model, just as in particle physics when many different phenomena are reduced to a few convergent parameters to test the model. There are yet a still highly discrepant results on , but it is not too difficult to speculate their origins. On the other hand, the current `low ' means the values that vary almost by a factor of three and effort is needed to make these converge.

Table 9. Summary of and .

method	0	?	model used?
H0 vs t0	< 0.7
luminosity density +M/L	0.1-0.4
cluster baryon fraction	0.15-0.35
SNeIa Hubble diagram	0.3	0.7
small-scale velocity field (summary)	0.2±0.15
(pairwise velocity)	0.15±0.1
(Local Group kinematics)	0.15±0.15
(Virgocentric flow)	0.2±0.2
large-scale vel field	0.2-1
cluster evolution (low sol'n)	0.2+0.3-0.1		yes
(high sol'n)	~ 1		yes
COBE-cluster matching	0.35-0.45 (if = 0)		yes
	0.20-0.40 (if 0)		yes
shape parameter	0.2-0.4		yes
CBR acoustic peak	free (if flat)	- 2	yes
	> 0.5 (if open)		yes
gravitational lensing	< 0.8
summary	0.15-0.45 (if open)
	0.2-0.4 (if flat)
		0.6-0.7(?)

The cosmological constant has been an anathema over many years because of our ignorance of any mechanism that could give rise to a very small vacuum energy of (3 meV)⁴, and neither can we understand a zero cosmological constant. In mid-nineties the atmosphere was changing in favour for a non-zero . The prime motivation was the Hubble constant-age problem, but the introduction of a non-zero was helpful in many respects. One theoretical motivation was to satisfy flatness which is expected in inflationary scenarios (Peebles 1984). Ostriker & Steinhardt (1995) proclaimed a `cosmic concordance' with a flat universe mildly dominated by . By 1997, only one observation contradicted with the presence of a moderate value of ; this was the SNeIa Hubble diagram presented by the Supernova Cosmology Project (Perlmutter et al. 1997); see Fukugita 1997. In the next two years the situation changed. Two groups analysing SNeIa Hubble diagram, including the Supernova Cosmology Project, now claim a low and a positive . On the other hand, the Hubble constant-age problem became less severe due to our cognition of larger uncertainties, especially in the age estimate. The indications from SNeIa Hubble diagram are very interesting and important, but the conclusions are susceptible to small systematic effects. They should be taken with caution. We should perhaps wait for small-scale CBR anisotropy observations to confirm a nearly flat universe before concluding the presence of .

In these lectures we have not considered classical tests, number counts, angular-size redshift relations, and magnitude-redshift relations of galaxies (Sandage 1961; 1988), in those testing for and . Unlike clusters or large scale structure, where no physics other than gravity plays a role, the evolution of galaxies is compounded by rich physics. Unless we understand their astrophysics, these objects cannot be used as testing candles. It has been known that galaxy number counts is understood more naturally with a low matter density universe under the assumption that the number of galaxies are conserved, but it is possible to predict the correct counts with an = 1 model where galaxies form through hierarchical merging, by tuning parameters that control physics (Cole et al. 1994; Kauffmann et al. 1994). It is important to work out whether the model works for any cosmological parameters or it works only for a restricted parameter range. This does not help much to extract the cosmological parameters, but it can falsify the model itself.

We have seen impressive progress in the determination of the Hubble constant. The old discrepancy is basically solved. On the other hand, a new uncertainty emerged in more local distance scales. The most pressing issue is to settle the value of the distance to LMC. There are also a few issues to be worked out should one try to determine H₀ to an accuracy of a 10% error or less. They include understanding of metallicity effects and interstellar extinction. The future effort will give more weight to geometric or semi-geometric methods. From the view point of observations the work will go to infra-red colour bands to minimise these problems.

In conclusion, I present in Figure 6 allowed ranges of H₀ and (and ) for the case of (a) flat and (b) open universes. With the flat case we cut the lower limit of at 0.2 due to a strong constraint from lensing. An ample amount of parameter space is allowed for a flat universe. A high value of H₀ > 82, which would be driven only by a short LMC distance, is excluded by consistency with the age of globular clusters as noted earlier. Therefore, we are led to the range H₀ 60-82 from the consistency conditions. For an open universe the coeval-formation interpretation is compelling for globular clusters, or else no region is allowed. The allowed H₀ is limited to 60-70. No solution is available if LMC takes a short distance.

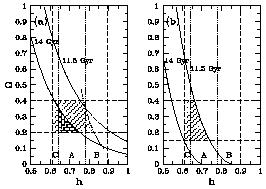
Figure 6. Consistent parameter ranges in the H0 - space for (a) a flat universe and (b) an open universe. A is the range of the Hubble constant when (m - M)LMC = 18.5. B or C is allowed only when the LMC distance is shorter by 0.3 mag, or longer by 0.1 mag. Note in panel (a) that most of the range of B is forbidden by the compatibility of age and H0 that are simultaneously driven by the RR Lyr calibration (section 2.7). Also note that the age range between 11.5 Gyr and 14 Gyr is possible only with the interpretation that globular cluster formation is coevel (section 2.4). The most naturally-looking parameter region is given a thick shade.