5.1. The Galaxy Two-Point Correlation Function
The simplest approach to clustering is to ask how much does it differ
from a uniform distribution at the two-point level, or in other words,
which is the
excess probability over random to find a galaxy at a separation
r from another galaxy. This is one way in which the two-point
correlation function
 (r) can be defined (see
[72]
for a more detailed introduction). The first estimates of the two-point
correlation function go back to the seventies
[73],
but the lack of large redshift samples limited these early analyses
to the angular correlation function
w(
(r) can be defined (see
[72]
for a more detailed introduction). The first estimates of the two-point
correlation function go back to the seventies
[73],
but the lack of large redshift samples limited these early analyses
to the angular correlation function
w( ). This is
related to
). This is
related to  (r)
through the Limber equation
[72]
(r)
through the Limber equation
[72]

| (2)
|
where  is the radial selection
function expected for the 2D survey being analysed.
is the radial selection
function expected for the 2D survey being analysed.
The basic description of galaxy clustering that emerged from these works
is still valid today on small and intermediate scales:
w( ) is well described by
a power law
) is well described by
a power law 
 -0.8, corresponding
to a spatial correlation function
(r /
r0)-
-0.8, corresponding
to a spatial correlation function
(r /
r0)- , with
r
, with
r  5
h-1 Mpc and
5
h-1 Mpc and

 - 1.8,
and a break with a rapid decline to zero around
r ~ 10 - 20 h-1 Mpc. As we shall discuss in the
following, modern surveys have significantly improved our knowledge of
the two-point correlation functions especially on scales
> 10 h-1 Mpc.
However, before discussing these most recent results, it is important
to briefly describe how galaxy peculiar velocities affect the
observed shape of
- 1.8,
and a break with a rapid decline to zero around
r ~ 10 - 20 h-1 Mpc. As we shall discuss in the
following, modern surveys have significantly improved our knowledge of
the two-point correlation functions especially on scales
> 10 h-1 Mpc.
However, before discussing these most recent results, it is important
to briefly describe how galaxy peculiar velocities affect the
observed shape of  (r) .
(r) .
5.1.1. REDSHIFT SPACE DISTORTIONS
The actual detection of true intrinsic deviations of
 (s) from a power
law is complicated in the analysis of redshift surveys by the effects
induced by
galaxy peculiar velocities. Here s is now used to make it explicit
that separations are in reality not measured in true 3D space, but in
redshift space: what we actually measure when we take the
redshift of a galaxy is the quantity
cz = cztrue + vpec//,
where
vpec// is the component of the galaxy peculiar velocity
along the line of sight. This component, while typically
~ 100 km s-1 for ``field'' galaxies, can rise
above 1000 km s-1 in rich
clusters of galaxies. This distorts the real-space correlation
function in different ways, depending on the scale.
The resulting
(s) from a power
law is complicated in the analysis of redshift surveys by the effects
induced by
galaxy peculiar velocities. Here s is now used to make it explicit
that separations are in reality not measured in true 3D space, but in
redshift space: what we actually measure when we take the
redshift of a galaxy is the quantity
cz = cztrue + vpec//,
where
vpec// is the component of the galaxy peculiar velocity
along the line of sight. This component, while typically
~ 100 km s-1 for ``field'' galaxies, can rise
above 1000 km s-1 in rich
clusters of galaxies. This distorts the real-space correlation
function in different ways, depending on the scale.
The resulting  (s) ,
is in general flatter than the real-space
(s) ,
is in general flatter than the real-space
 (r) . This is
the result of two competing effects:
the small-scale pairwise velocity dispersion, mostly dominated by
high-velocity pairs in clusters of galaxies (i.e. those within
the so-called ``Fingers of God''), damps the amplitude of
(r) . This is
the result of two competing effects:
the small-scale pairwise velocity dispersion, mostly dominated by
high-velocity pairs in clusters of galaxies (i.e. those within
the so-called ``Fingers of God''), damps the amplitude of
 (r) below
~ 3 h-1 Mpc.
On the other hand, coherent flows towards large-scale structures
enhance the contrast of those structures lying perpendicularly to
the line of sight, thus amplifying
(r) below
~ 3 h-1 Mpc.
On the other hand, coherent flows towards large-scale structures
enhance the contrast of those structures lying perpendicularly to
the line of sight, thus amplifying
 (s) in the
linear regime (i.e.
above 10 - 20 h-1 Mpc). I will not enter here into
details on how
the wealth of information on the dynamics of galaxies contained in
these distortions can be extracted, but limit myself to a discussion
on how to correct them to recover the true shape of
(s) in the
linear regime (i.e.
above 10 - 20 h-1 Mpc). I will not enter here into
details on how
the wealth of information on the dynamics of galaxies contained in
these distortions can be extracted, but limit myself to a discussion
on how to correct them to recover the true shape of
 (r) . A more
complete discussion can be found, e.g., in
[74] and
[51].
(r) . A more
complete discussion can be found, e.g., in
[74] and
[51].
Redshift space distortions can be corrected either at a rough
level, through a simple statistical compression of the ``Fingers of God''
(e.g. [75]),
or in a more
appropriate way by computing the correlation function
 (rp,
(rp,
 ) ,
where the separation vector s between two objects is split into two
components rp and
) ,
where the separation vector s between two objects is split into two
components rp and
 related as
s2 = rp2 +
related as
s2 = rp2 +
 2. This
two-dimensional correlation function can then be projected along the
line-of-sight direction, to obtain the function
2. This
two-dimensional correlation function can then be projected along the
line-of-sight direction, to obtain the function
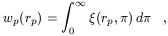
| (3)
|
which is independent of redshift-space distortions. We have already
encountered this function in Figure 6
when comparing the clustering strength of early- and late-type galaxies in real
space (and thus free of their rather different peculiar velocity
fields). wp(rp) can either be used
to constrain the parameters of a chosen model for
 (r) , as
e.g. the classical
(r) , as
e.g. the classical
 (r) = (r
/ r0)-
(r) = (r
/ r0)- [56],
or inverted through the Abel integral relations to recover the whole
[56],
or inverted through the Abel integral relations to recover the whole
 (r) .
(r) .
All these problems are obviously absent when one analyses
w( ), where on the other
hand the strongest uncertainty in the
de-projection lies in the knowledge of the radial selection function.
), where on the other
hand the strongest uncertainty in the
de-projection lies in the knowledge of the radial selection function.
5.1.2. THE LARGE-SCALE SHAPE OF
 (r)
The simple form observed from the first estimates of
w(
(r)
The simple form observed from the first estimates of
w( ) and
) and
 (r) at small
separations was consistent with the expectations of
gravitational growth from some initial spectrum of fluctuations (at
the time thought to possibly be a simple white-noise i.e.
(r) at small
separations was consistent with the expectations of
gravitational growth from some initial spectrum of fluctuations (at
the time thought to possibly be a simple white-noise i.e.
 k0, see
next section): as gravity has no
built-in preferential scale, a power law seemed to be a natural
consequence of gravitational clustering (see e.g.
[72]).
However, since then we have understood that plausible initial
conditions are all but a white-noise (see e.g. the first computation
of the linear power spectrum in a Universe dominated by Cold Dark Matter,
[76]),
so that the clustering we measure today with
k0, see
next section): as gravity has no
built-in preferential scale, a power law seemed to be a natural
consequence of gravitational clustering (see e.g.
[72]).
However, since then we have understood that plausible initial
conditions are all but a white-noise (see e.g. the first computation
of the linear power spectrum in a Universe dominated by Cold Dark Matter,
[76]),
so that the clustering we measure today with
 (r) is not just
the product of the nonlinear action of gravity.
(r) is not just
the product of the nonlinear action of gravity.
In Figure 9, I have plotted the estimates of
 (s) for
the ESP [77,
32],
the LCRS
[78], the
Stromlo-APM (Loveday et al. 1992b), and the Durham-UKST
[80]
surveys. These samples
represent a selection of data that should offer the best compromise
between depth and angular aperture, thus maximising the ability to
sample large scales. In addition, the dotted lines show a plot of
(s) for
the ESP [77,
32],
the LCRS
[78], the
Stromlo-APM (Loveday et al. 1992b), and the Durham-UKST
[80]
surveys. These samples
represent a selection of data that should offer the best compromise
between depth and angular aperture, thus maximising the ability to
sample large scales. In addition, the dotted lines show a plot of
 (r) obtained
through de-projection of the angular
w(
(r) obtained
through de-projection of the angular
w( ) from
the APM galaxy catalogue
[81]
under two different
assumptions about galaxy clustering evolution and thus selection function.
) from
the APM galaxy catalogue
[81]
under two different
assumptions about galaxy clustering evolution and thus selection function.
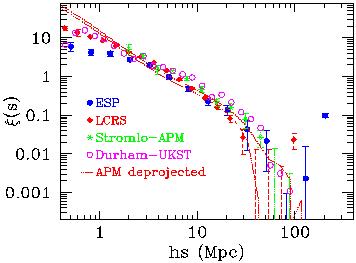
|
Figure 9. Recent estimates of the two-point
correlation function of
optically-selected galaxies. The plot shows results from the ESP
(Guzzo et al. 1998, 1999),
the LCRS (Tucker et al. 1997), the APM-Stromlo
[79]
and the Durham-UKST
[80]
surveys.
|
We clearly see how, within some scatter among different surveys,
 (s) remains
positive to separations of 50 h-1 Mpc
or larger. Keeping in mind how the variance in galaxy counts is ~ 1
around 8 h-1 Mpc, we can conclude that a significant
range of scales
over which we measure positive clustering is still in the linear or
quasi-linear regime.
(s) remains
positive to separations of 50 h-1 Mpc
or larger. Keeping in mind how the variance in galaxy counts is ~ 1
around 8 h-1 Mpc, we can conclude that a significant
range of scales
over which we measure positive clustering is still in the linear or
quasi-linear regime.
The global form below 5 - 10 h-1 Mpc is still well
described by a power law: the slope is very close to the classical
-1.8 for the APM
 (r) , which is
in real space, while it is flatter
for all the redshift-space measures due to the suppression by
peculiar velocities discussed above.
Above ~ 5 h-1 Mpc there is unanimous evidence for
more power than
expected by a simple extrapolation of the small-scale slope. This
``bump'' or ``shoulder'' is evident both in the APM
(r) , which is
in real space, while it is flatter
for all the redshift-space measures due to the suppression by
peculiar velocities discussed above.
Above ~ 5 h-1 Mpc there is unanimous evidence for
more power than
expected by a simple extrapolation of the small-scale slope. This
``bump'' or ``shoulder'' is evident both in the APM
 (r) and in the
redshift-space measures, implying that it is not an effect of the
expected redshift-space amplification by coherent flows
[82].
We found clear early evidence for this excess when
studying clustering in the Perseus-Pisces survey
[47],
and realised that it was present already in the published CfA1 data
(as also noticed in
[83]).
At the time we suggested
that it was and indication for a steep power spectrum P(k)
(r) and in the
redshift-space measures, implying that it is not an effect of the
expected redshift-space amplification by coherent flows
[82].
We found clear early evidence for this excess when
studying clustering in the Perseus-Pisces survey
[47],
and realised that it was present already in the published CfA1 data
(as also noticed in
[83]).
At the time we suggested
that it was and indication for a steep power spectrum P(k)
 k-2.2 on
large scales. Further theoretical modeling
[84]
and the new direct
measures of P(k) in real space from the APM survey
[85],
confirmed that indeed there is a significant change in
k-2.2 on
large scales. Further theoretical modeling
[84]
and the new direct
measures of P(k) in real space from the APM survey
[85],
confirmed that indeed there is a significant change in
 (r)
around r
(r)
around r  3 - 5
h-1 Mpc. It was natural to interpret this as a
consequence of the transition between the strongly nonlinear
clustering regime at small separations, to a quasi-linear regime on
larger scales. In Section 5.3 we shall come back to
this point
while discussing directly the observed shape of P(k).
3 - 5
h-1 Mpc. It was natural to interpret this as a
consequence of the transition between the strongly nonlinear
clustering regime at small separations, to a quasi-linear regime on
larger scales. In Section 5.3 we shall come back to
this point
while discussing directly the observed shape of P(k).
5.2. The Clustering of Clusters
We have seen that clusters of galaxies represent a powerful tracer of
structure on the largest possible scales. Their clustering can be also
quantified at the simplest level through the two-point correlation
function. The classic estimate of
 (s) for Abell clusters
[86]
showed that the cluster-cluster
correlation function is also well described by a power law, with a slope
apparently similar to that of galaxies, but a correlation length
about 4 times larger. In reality, due to the limited size of the
sample, the original fit was performed imposing a slope
(s) for Abell clusters
[86]
showed that the cluster-cluster
correlation function is also well described by a power law, with a slope
apparently similar to that of galaxies, but a correlation length
about 4 times larger. In reality, due to the limited size of the
sample, the original fit was performed imposing a slope
 = 1.8,
and therefore it was not really a measure of the functional shape of
cluster-cluster correlations.
Nevertheless, the fit was good enough, and it became generally accepted that
the cluster-cluster correlation function has a the same slope as galaxies,
= 1.8,
and therefore it was not really a measure of the functional shape of
cluster-cluster correlations.
Nevertheless, the fit was good enough, and it became generally accepted that
the cluster-cluster correlation function has a the same slope as galaxies,
 = 1.8, but larger
amplitude (see e.g.
[60]),
that is
= 1.8, but larger
amplitude (see e.g.
[60]),
that is
 cc(r)
cc(r)
 A .
A .
 gg(r).
In fact, this statement could
not rigorously be true if
a simple statistical amplification mechanism, as then suggested by
Kaiser [60],
were the origin of the different amplitude: clusters
trace scales > 10 h-1 Mpc, i.e. cover mostly
fluctuations that are in the
quasi-linear or linear regime, and it would have been a rather
strange conspiracy, that their slope were the same that galaxies
display on scales between 0.1 and 5 h-1 Mpc, where
clustering is highly nonlinear.
gg(r).
In fact, this statement could
not rigorously be true if
a simple statistical amplification mechanism, as then suggested by
Kaiser [60],
were the origin of the different amplitude: clusters
trace scales > 10 h-1 Mpc, i.e. cover mostly
fluctuations that are in the
quasi-linear or linear regime, and it would have been a rather
strange conspiracy, that their slope were the same that galaxies
display on scales between 0.1 and 5 h-1 Mpc, where
clustering is highly nonlinear.
The basic problem was that the galaxy correlation function was not known
accurately enough on large scales, as to provide a meaningful
comparison. The situation has fortunately improved significantly since
then. We have just reviewed the significant progress made in our knowledge of
the galaxy correlation function. In parallel, new cluster samples
have been constructed, such as the EDCC
[87]
and APM [89]
automatically selected cluster catalogues, and the quality and number
of redshifts available for Abell clusters have substantially increased.
Although I will not enter into details concerning optically-selected
clusters, in Figure 10 I have reproduced a plot from
[61],
showing an up-to-date comparison of the
cluster-cluster correlation functions of both an Abell sample
[88],
and a sample of APM clusters
[89].
While comparison is presented with two possible power laws, the data clearly
show a break from these simple models around 50 h-1
Mpc, much in the same way as galaxies do on a similar scale. See
[61]
for more details.
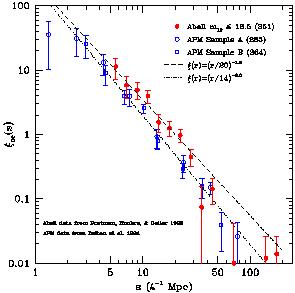
|
Figure 10. The cluster-cluster correlation
function optically-selected
clusters from the Abell and APM catalogues, reproduced from the review
by Postman
[61].
|
In section Section 4.1 I argued that X-ray
selection is
the best way to select homogeneous samples of clusters with
well-defined physical criteria out to large redshifts. In particular, X-ray
luminosity is a parameter that is much more closely related to mass than the
somewhat loosely defined richness, used to characterise
optically-selected clusters. For this reason, model predictions for
the clustering of massive objects, can be more easily and safely translated in
terms of observable quantities as luminosities and fluxes, than in the
case of galaxies
[90].
At a simpler observational level, it
is particularly interesting to compare
 cc for X-ray
selected clusters
to that of galaxies, as we do in Figure 11
[91].
This figure shows a preliminary estimate of
cc for X-ray
selected clusters
to that of galaxies, as we do in Figure 11
[91].
This figure shows a preliminary estimate of
 cc from the
flux-limited REFLEX survey
[92],
compared to the galaxy-galaxy
correlation function from two volume-limited subsamples of the ESP
survey
[32]
(11) .
The dashed line on top of the cluster points is the Fourier
transform of the power spectrum of REFLEX clusters (computed
independently, see next section) while the bottom line has been
scaled down by an
arbitrary factor bcg2 = (3.3)2,
so as to overlap the galaxy
points. The agreement
between the shapes of the cluster and galaxy correlation functions is
remarkable. Here we also see how a proper functional description of
the shape is not just a simple power law. The one shown here is the
Fourier transform of the simple phenomenological shape for P(k)
suggested by Peacock
[51].
cc from the
flux-limited REFLEX survey
[92],
compared to the galaxy-galaxy
correlation function from two volume-limited subsamples of the ESP
survey
[32]
(11) .
The dashed line on top of the cluster points is the Fourier
transform of the power spectrum of REFLEX clusters (computed
independently, see next section) while the bottom line has been
scaled down by an
arbitrary factor bcg2 = (3.3)2,
so as to overlap the galaxy
points. The agreement
between the shapes of the cluster and galaxy correlation functions is
remarkable. Here we also see how a proper functional description of
the shape is not just a simple power law. The one shown here is the
Fourier transform of the simple phenomenological shape for P(k)
suggested by Peacock
[51].
The result shown in Figure 11 is a powerful
confirmation of a
simple linear bias model between galaxies and clusters of galaxies,
analogous to eq. (1), as first suggested by Kaiser
[60]
(see also
[93]
for a more recent refinement). Indeed, considering the relationship between
 (r) and
the variance within a top-hat sphere of radius r
(r) and
the variance within a top-hat sphere of radius r

| (4)
|
eq. (1) implies that the cluster and galaxy correlation
functions obey to the relation
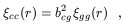
| (5)
|
where the relative bias factor bcg is related to the
typical mass of the clusters considered
[60].
This kind of
investigation can be generalised to the study of the dependence of the
correlation length on the sample limiting X-ray luminosity, for which
also model predictions can be quite specific
[93].
This will also be an important output of the REFLEX survey
[92].

|
Figure 11. Comparison of the two-point
correlation functions of REFLEX clusters
[92]
and ESP galaxies
[32].
The top dashed line is the Fourier transform of a simple
phenomenological fit of the REFLEX power spectrum with a
double-power-law model. The bottom one is the same after scaling by
an arbitrary bias factor of
bc2 = (3.3)2. The agreement in shape
between galaxies and clusters is remarkable. At the same time, both
galaxies and clusters show an indication, after the breakdown around
r  50
h-1 Mpc, for more positive power on scales exceeding
100 h-1 Mpc. 50
h-1 Mpc, for more positive power on scales exceeding
100 h-1 Mpc.
|
5.3. The Power Spectrum
The Fourier transform of the correlation function is the power spectrum
P(k)
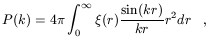
| (6)
|
which describes the distribution of power among different wavevectors
or modes k = 2 /
/
 once we decompose the fluctuation field
once we decompose the fluctuation field
 =
=

 /
/
 over the Fourier basis
[51].
over the Fourier basis
[51].
The amount of information contained in P(k) is thus formally the
same yielded by the correlation function. The estimates of
P(k) or
 (r)
from redshift surveys, however, are affected in different ways by
uncertainties introduced, for example, by the poor knowledge of the
mean density (in which case the power spectrum is to be preferred),
or by the shape of the survey volume (whose effect is usually more
easily treated when computing
(r)
from redshift surveys, however, are affected in different ways by
uncertainties introduced, for example, by the poor knowledge of the
mean density (in which case the power spectrum is to be preferred),
or by the shape of the survey volume (whose effect is usually more
easily treated when computing
 (r) rather than
P(k)). Useful
references for learning more about this topic are
[94],
[7] and
[51],
where further
directions can be found to specific technical papers.
One practical benefit of the description of clustering in Fourier
space through P(k) is that for fluctuations of very
long spatial wavelength (
(r) rather than
P(k)). Useful
references for learning more about this topic are
[94],
[7] and
[51],
where further
directions can be found to specific technical papers.
One practical benefit of the description of clustering in Fourier
space through P(k) is that for fluctuations of very
long spatial wavelength ( > 100 h-1 Mpc), where
> 100 h-1 Mpc), where
 (r) is dangerously
close to zero and errors easily make the measured values fluctuate
around it, P(k) is on the contrary very large.
Around these scales, most models predict the power spectrum to have a
maximum, which reflects the size of the horizon at the epoch of
matter-radiation equivalence.
(r) is dangerously
close to zero and errors easily make the measured values fluctuate
around it, P(k) is on the contrary very large.
Around these scales, most models predict the power spectrum to have a
maximum, which reflects the size of the horizon at the epoch of
matter-radiation equivalence.
Indeed, comparison of observations to the theory is in
principle easier and more direct using P(k). First, models
are usually
specified in terms of a linear P(k), which is the result
of the action
of the specific transfer function of the model on a primordial
spectrum, usually assumed to be of the so-called
Harrison-Zel'dovic scale-invariant form
 k1, which is also
the kind of spectrum most naturally produced in inflationary scenarios
(see e.g.
[50]
for more details). In addition, k-modes in
Fourier space are statistically independent (a part from the
convolution effects due to the window function of the survey,
see below), and direct
k1, which is also
the kind of spectrum most naturally produced in inflationary scenarios
(see e.g.
[50]
for more details). In addition, k-modes in
Fourier space are statistically independent (a part from the
convolution effects due to the window function of the survey,
see below), and direct  2
comparisons to models is feasible,
which is in principle not the case when the correlation function is
analysed (see e.g.
[95]).
2
comparisons to models is feasible,
which is in principle not the case when the correlation function is
analysed (see e.g.
[95]).
However, not everything is better with power spectra. Redshift surveys
are all but cubes (i.e. what would be optimal for a Fourier
plane-wave decomposition), and their geometrical shape affects the
measured power, so that what we really measure is the quantity
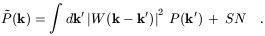
| (7)
|
The measured power spectrum is therefore a convolution of the
true P(k) with the square modulus of the window
function |W(k)|2 , that is the Fourier
transform of the survey volume, plus an additional shot-noise term.
While the shot-noise contribution SN is easily corrected for, the
recovery of the true P(k)
necessarily involves a delicate de-convolution operation in k
space. While for nearly tridimensional surveys (as IRAS-based surveys
[96,
97,
98],
or the CfA2-SSRS2
[99],
Stromlo-APM
[100],
Durham-UKST
[101],
and REFLEX surveys), the effect of the
window function is mostly negligible, for nearly two-dimensional surveys as
the LCRS or, even worse, the ESP, its effect is dramatic to very small
wavelengths. The key point is that for slice surveys like ESP, the
window function is very anisotropic, in particular it is extremely large
along the direction perpendicular to the main plane of the survey.
When the final
estimate of P(k) is computed by averaging over the whole
4 solid
angle, this anisotropy brings contributions from different k's
into the same averaged k bin. It is important to keep these
limitations in mind when one compares estimates of P(k)
from different
surveys as we shall do here. A comprehensive discussion
on different estimators for P(k) and how to take these
effects into account can be found in
[102].
solid
angle, this anisotropy brings contributions from different k's
into the same averaged k bin. It is important to keep these
limitations in mind when one compares estimates of P(k)
from different
surveys as we shall do here. A comprehensive discussion
on different estimators for P(k) and how to take these
effects into account can be found in
[102].
A different approach for dealing with surveys with peculiar shapes is
otherwise that suggested by Vogeley & Szalay
[103],
using the so-called Karhunen-Loève transform. Rather than trying to
correct the effect of the window function over the plane waves of the Fourier
basis, the idea is to find a different set of orthonormal eigenvectors
which are optimal given the survey geometry. The interesting
quantities, as e.g. P(k), are then projected on this
basis, both for
the data and for the models, and comparison is performed through a
maximum likelihood analysis. Application of this method has been so
far limited only to the 2D case
[103].
A first application to the REFLEX data
[105]
is yielding promising results.
5.3.1. THE POWER SPECTRUM OF THE GALAXY
DISTRIBUTION
In Figure 12, I have plotted the estimates of
P(k) for the
same surveys as given in Figure 9
(12) .
The four data sets allow me
also to make a comparison of estimates from relatively tridimensional surveys
(Stromlo-APM, Durham-UKST), to more bidimensional samples as the LCRS
and ESP, the latter being in practice a single thin slice cut through
the galaxy distribution. This means that the effect of the window
function (and the need of a proper correction) on these data sets is
very different. In addition, three of the four samples are selected
in exactly the same photometric band, the blue-green
bJ (two, ESP
and Durham-UKST are even constructed from the same catalogue, the
EDSGC), the only exception being the r-band selected LCRS. This has the
positive effect of reducing the relative biasing between the different
samples, although some effect is possibly still present due to the
different luminosity ranges covered.
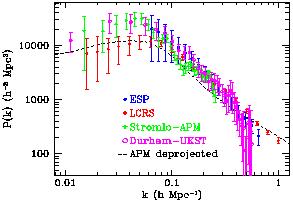
|
Figure 12. A non-exhaustive compilation of
most recent estimates of the
power spectrum of galaxy clustering, from four of the largest
available redshift surveys of optically-selected galaxies (ESP
[106];
LCRS
[107];
Stromlo-APM
[100];
Durham-UKST
[101]),
compared to that deprojected (and therefore in real space), from the 2D
APM galaxy survey
[85].
|
In the same figure, I have also plotted (dashed line) P(k) as
reconstructed from the projected angular clustering of the APM galaxy
catalogue
[85].
This is clearly the only
estimate which is free of redshift-space distortions. The effect of
these is shown
in particular by the slope above ~ 0.3 h Mpc-1: an increased
slope in real space (dashed line) corresponds to a stronger damping by
peculiar velocities, diluting the apparent clustering observed in redshift
space (all points).
The first impression from this comparison is that to first order there
is quite a good agreement across the different samples. The general trend is
that of a well-defined power law range between ~ 0.08 and
~ 0.3 h Mpc-1, with a slope around
k-2. Note that despite these
samples are rather similar in terms of their galaxy properties, a
minimal level of relative biasing might be present because of the
relative weight of faint and bright objects. The only two samples that
should in principle display the same amplitude are the ESP and the
Durham-UKST surveys, which are both selected from the EDSGC catalogue.
In fact, their P(k) are
practically identical over a good range of k's. On one hand, the
Durham-UKST P(k) becomes rather noisy at small scales, due to the
sparse sampling strategy of this survey (less sparse than the
Stromlo-APM, though). On the other hand, the ESP P(k)
performs well
on small scales, but on large scales it has to be limited to
k > 0.06 h Mpc-1,
below which the effect of its nasty window function cannot be
deconvolved appropriately. In fact, the very good agreement with the
Durham-UKST down to fairly small k's is a very encouraging
indication of the quality of the deconvolution procedure performed by
the authors
[106].
We also note how the LCRS power spectrum tends to be flatter and of
lower amplitude around the tentative turnover displayed by the
Durham-UKST and Stromlo-APM spectra. Also at large k's, where ESP
and Durham-UKST are significantly damped by small-scale pairwise
velocities, the LCRS P(k) seems to be less affected by
this distortion.
The same trend is also visible in the correlation function plot of
Figure 9.
Recalling the discussion of Section 5.1 on the shoulder
observed in the two-point correlation function above
~ 5 h-1 Mpc,
here we can see clearly the same effect in P(k) by looking at the
real-space power spectrum from the APM
catalogue. The slope of the APM P(k) above 0.3 h
Mpc-1 is
~ k-1.2, corresponding to the small-scale clustering
regime (in real space!) where

 - 1.8. Below this scale,
P(k) steepens to
~ k-2, and this is what produces the excess power
in
- 1.8. Below this scale,
P(k) steepens to
~ k-2, and this is what produces the excess power
in  (s) on large
scales.
(s) on large
scales.
Peacock [108]
applied the sophisticated linear
reconstruction machinery by Hamilton and collaborators
[109]
to the whole P(k)
from the APM catalogue (and to another real-space estimate from the
the IRAS-QDOT survey
[110])
and concluded that the
shape was indeed consistent with a linear power spectrum
characterised by a steep slope (~ k-2.2). This is the same
value of linear slope originally suggested in
[47] to
explain the observed large-scales shape of
 (s) in the
CfA1 and Perseus-Pisces redshift surveys, and
confirms the early speculation that the observed change in slope of
(s) in the
CfA1 and Perseus-Pisces redshift surveys, and
confirms the early speculation that the observed change in slope of
 (r) is a
manifestation of the transition from the quasi-linear to the
strongly nonlinear clustering regime.
(r) is a
manifestation of the transition from the quasi-linear to the
strongly nonlinear clustering regime.
5.3.2. THE POWER SPECTRUM FROM CLUSTERS
Also for measuring the power spectrum, clusters of galaxies
offer the most efficient alternative to galaxies, given their ability
to sample very large volumes.
A first preliminary estimate of P(k) from the REFLEX
survey is shown in Figure 13
[105],
compared to the power
spectra of the largest redshift sample available for Abell clusters
[111],
and that of the APM automatic optically-selected clusters
[112].
This is a conservative measure, based
on only 188 of the nearly 460 clusters with redshifts that will form
the final REFLEX sample, using a Fourier box of 400 h-1 Mpc
comoving side. This was done to avoid possible spurious fluctuations
due to the incomplete sampling between the Northern and the Southern
galactic sides of the survey. At the time of writing this review,
virtually all clusters in the survey have been observed
spectroscopically. A new measure of P(k) in a box of
~ 1000 h-1 Mpc side (i.e. using all clusters within
z ~ 0.2, where
the survey is complete), should be produced by the
end of 1999 (13) .
Despite the point at smaller k's is not significant,
the turnover around k  0.05 h Mpc-1 is shown to be significant at
the 3
0.05 h Mpc-1 is shown to be significant at
the 3 level by a Karhunen-Loéve
[103]
Maximum Likelihood analysis
(14) .
The analysis of the whole survey
should also allow to put more serious constraints on the detailed
shape of P(k) around the turnover.
level by a Karhunen-Loéve
[103]
Maximum Likelihood analysis
(14) .
The analysis of the whole survey
should also allow to put more serious constraints on the detailed
shape of P(k) around the turnover.
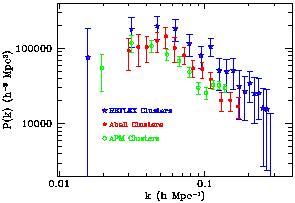
|
Figure 13. The power spectrum of the
clustering of clusters, as measured
from three different cluster surveys: a preliminary subsample of 188
clusters from the X-ray selected REFLEX survey
[105], and
redshift samples from the Abell
[111],
and APM
[112] cluster catalogues. Note that a systematic
difference in amplitude among these surveys is expected as they sample
different mass thresholds, and are therefore characterised by
different bias values.
|
5.4. Features in the Power Spectrum
During the last few years, evidence has indeed been accumulating
that the peak of the power spectrum could be rather sharp, perhaps
characterised by an extra feature (with respect to smooth traditional models)
around its maximum. Einasto and collaborators
[114]
analysed the distribution of Abell clusters, finding evidence
for a sharp peak around
k  0.05 h
Mpc-1. Although their result was
questioned by other workers because of the possible incompleteness in
the sample and the way P(k) was estimated, the presence of such a
feature was confirmed by a more conservative reanalysis of Abell data
[111],
where a slightly less pronounced but still
significant peak is found, as we show in Figure 13.
The peak is indeed evident in the Abell data, while the preliminary
REFLEX sample is not yet able to put serious constraints on the shape
around the turnover. Note also the very good agreement of the slopes
of the three power spectra above
k
0.05 h
Mpc-1. Although their result was
questioned by other workers because of the possible incompleteness in
the sample and the way P(k) was estimated, the presence of such a
feature was confirmed by a more conservative reanalysis of Abell data
[111],
where a slightly less pronounced but still
significant peak is found, as we show in Figure 13.
The peak is indeed evident in the Abell data, while the preliminary
REFLEX sample is not yet able to put serious constraints on the shape
around the turnover. Note also the very good agreement of the slopes
of the three power spectra above
k  0.5 h
Mpc-1, and
at the same time the shift in amplitude of the three samples. The
latter is a clear manifestation, again, of the different bias of the
three samples. An X-ray selected sample as REFLEX allows for a more
direct link to the typical mass of the objects we are looking at (see
[115],
for a more extended discussion of these points).
0.5 h
Mpc-1, and
at the same time the shift in amplitude of the three samples. The
latter is a clear manifestation, again, of the different bias of the
three samples. An X-ray selected sample as REFLEX allows for a more
direct link to the typical mass of the objects we are looking at (see
[115],
for a more extended discussion of these points).
If we also recall that evidence for excess power around
~ 100 h-1 Mpc was provided by a 2D power spectrum
analysis of the LCRS slices
[116],
we cannot avoid being amused by the consistency
in the peak scale to which these separate measures point, i.e.,
consistently between 100 and 150 h-1 Mpc. This is
remarkably close to the
``periodicity'' scale revealed by Broadhurst and collaborators
([117],
BEKS hereafter), in the analysis
of their 1-dimensional pencil-beam surveys towards the galactic poles.
This latter result has certainly been one of the most exciting findings of
this decade in the study of large-scale structure. The authors merged
together two deep redshift surveys of redshifts performed
independently in the direction the two galactic poles over a small
field of ~ 0.7 degrees, exploring a total 1-dimensional
baseline of
~ 2000 h-1 Mpc. The resulting galaxy distribution showed
a surprising regularity of ``spikes''. The visual impression was
quantified and confirmed by a 1D correlation and power spectrum
analysis, that clearly indicated a preferential ``fluctuation'' at
128 h-1 Mpc.
This result originated significant controversy. It was suggested that it
could just be an aliasing of power due to the small size of the beam, that
projected power from small to large scales
[118].
On the other hand, the reality of the effect was supported by independent
observations showing how the more nearby peaks detected in the pencil beam
were coincident with known, real large-scale structures, as the Great
Wall or the Sculptor supercluster (e.g.
[119]).
Further pencil beams in different directions (e.g.
[120]),
and a denser sampling around the original pointings
[121]
also show that, yes, this direction is somewhat special, but
only in the sense that here the effect is maximised. This is
what one would statistically expect if there is indeed a distribution
of typical ``cell'' sizes around a characteristic dimension
[122].
The peak observed in the 3D
power spectrum of Abell clusters around the same scale is further
suggesting that the origin of the BEKS periodicity lies indeed in a
specific feature in the 3D power distribution around this wavelength.
Note also in Figures 9,
10
and 11 the
behaviour of the two-point correlation functions on very large
scales, for both galaxies and clusters. Although the binning of
 (s) is very
coarse at these separations, there is a hint that
(s) is very
coarse at these separations, there is a hint that
 (s) becomes
positive again around
150 - 200 h-1 Mpc. This seems to be common to
nearly all surveys,
independently of their geometry (slice or 3D surveys), the kind of
tracer (galaxy or clusters), and the estimator used. As can be
readily seen by Fourier
transforming a ``standard'' P(k) (e.g., a CDM shape
[123]),
this damped oscillation of
(s) becomes
positive again around
150 - 200 h-1 Mpc. This seems to be common to
nearly all surveys,
independently of their geometry (slice or 3D surveys), the kind of
tracer (galaxy or clusters), and the estimator used. As can be
readily seen by Fourier
transforming a ``standard'' P(k) (e.g., a CDM shape
[123]),
this damped oscillation of
 (s) cannot be
reproduced if
P(k) has a smooth turnover around its maximum, and seems to be a
further hint for a sharp peak. A similar oscillation in the
correlation function was claimed for Abell clusters
[124],
and interpreted as evidence for a sharp feature in P(k).
(s) cannot be
reproduced if
P(k) has a smooth turnover around its maximum, and seems to be a
further hint for a sharp peak. A similar oscillation in the
correlation function was claimed for Abell clusters
[124],
and interpreted as evidence for a sharp feature in P(k).
At the time of writing this review (Spring '99), one very interesting
piece of evidence has been provided along the same lines by Broadhurst
and Jaffe
[125],
who analyse the redshift distribution of the
high-redshift samples of Lyman-break selected galaxies by Steidel
and collaborators
[57].
As shown in
Figure 14, they find again the same
effect detected at smaller redshift, i.e. the emergence of a preferred
clustering scale. One important consequence is that the co-moving
scale of the peak in the power spectrum measured locally (
~ 130 h-1 Mpc), can be used as a standard stick to
provide a constrain on
the combination of
 M and
M and

 :
48
:
48 M -
15
M -
15

 10.5, which for a flat Universe
(
10.5, which for a flat Universe
( M +
M +

 = 1), gives
= 1), gives
 M = 0.4 ± 0.1.
M = 0.4 ± 0.1.
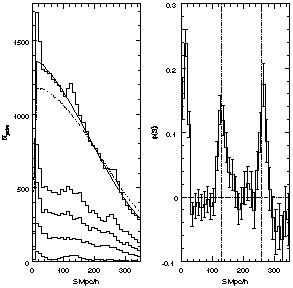
|
Figure 14. The one-dimensional clustering
of Lyman-break galaxies, from
[125].
Left: the co-added pair counts from
5 fields at z ~ 3 (top histogram), compared to the expectations
from a randomly distributed sample with the same selection function
(solid line). Right: the 1D correlation function along the line of
sight, showing the clear pattern with ~ 130 h-1 Mpc
periodicity (using  = 0.2). See
[125]
for details. = 0.2). See
[125]
for details.
|
The convergence of so many independent observations seems to have left
little doubt, in my opinion, that the observed characteristic scale is
real, and is telling us something important about the properties of
our Universe. Indeed, on the theory side
there has been considerable interest in the
recent literature about the possibile relation of this peak to baryonic
acoustic features produced within the last scattering surface
at z ~ 1000, when the Cosmic Microwave Background (CMB) radiation
originated. Eisenstein and collaborators
[126], show
however how a large baryon
fraction ( b /
b /
 0
0
 0.3 or larger), and a rather
ad hoc combination of parameters (as e.g. a ``blue'' tilt of the
primordial spectrum) are required to match the observed Abell peak, while
at the same time being consistent with the cluster
abundance (15) .
More dramatically, it is worrying to see that no realistic CDM
parameter combination is capable to account for the excess power (the
``shoulder'') we were discussing in section 5.1, that is
displayed by virtually all modern surveys
[127].
0.3 or larger), and a rather
ad hoc combination of parameters (as e.g. a ``blue'' tilt of the
primordial spectrum) are required to match the observed Abell peak, while
at the same time being consistent with the cluster
abundance (15) .
More dramatically, it is worrying to see that no realistic CDM
parameter combination is capable to account for the excess power (the
``shoulder'') we were discussing in section 5.1, that is
displayed by virtually all modern surveys
[127].
Even without considering the existence of extreme features, therefore
there seems to be a general difficulty for the ``standard'' theory to
explain the
detailed shape of P(k), now that the data are becoming of
higher and higher quality in the linear regime. Especially when
one tries matching the power spectrum implied by the growing amount
of CMB anisotropy experiments to that
displayed by the clustering of luminous matter, problems seem to be
unavoidable. According, for example, to Silk & Gawiser
[128]
``If the data are accepted as being mostly free of systematics and ad
hoc additions to the primordial power spectrum are avoided, there
is no acceptable model for large-scale structure.'' Once again, a
major uncertainty prevents any firm statement from being made: are we
allowed to compare the power spectrum derived from the distribution of light to
that derved from the mass (CMB), through a simple linear bias scaling?
Clearly, a
scale-dependent bias would add room for any detailed match between
models and the data, but without a solid physical basis would also add
an unpleasant ad hoc taste to the whole picture. In
addition, the extremely linear relation between the correlation
functions of galaxies and clusters that we have shown in
Figure 11, seems to suggest that at least above
~ 5 h-1 Mpc the galaxy and mass distributions are
linked by a simple linear bias.
11 The use of
volume-limited samples is to be preferred when discussing the shape of
 (s) .
Estimates of
(s) .
Estimates of
 (s) from whole
magnitude-limited surveys are
normally subject to weighting schemes, as e.g. the so-called J3
minimum-variance weighting, which, while allowing a better sampling
of very large scales, can affect the globale shape of
(s) from whole
magnitude-limited surveys are
normally subject to weighting schemes, as e.g. the so-called J3
minimum-variance weighting, which, while allowing a better sampling
of very large scales, can affect the globale shape of
 (s)
(Guzzo et al. 1999).
Volume-limited samples are much better defined in terms
of the properties of the galaxies they include, containing only
objects with luminosity above a well-defined threshold.
Back.
(s)
(Guzzo et al. 1999).
Volume-limited samples are much better defined in terms
of the properties of the galaxies they include, containing only
objects with luminosity above a well-defined threshold.
Back.
12 One further
notable estimate, not shown here, has been recently produced from the
IRAS-based PSCz survey, and can be found in
[104].
Back.
13 Note added in proof: a new estimate
of P(k) within such a volu
me obtained just before completing the final version
of this paper, can be found in
[113]
Back.
14 That is, projecting the data and a
phenomenological
form for P(k), with two power laws connected at a scale
xc, over the
best basis of eigenvectors found for the REFLEX geometry
[105].
Back.
15 Note added in proof: a similar model
is found to
provide a good description of the most recent estimate of
P(k) from the REFLEX data
[113].
Back.






 (r) can be defined (see
[72]
for a more detailed introduction). The first estimates of the two-point
correlation function go back to the seventies
[73],
but the lack of large redshift samples limited these early analyses
to the angular correlation function
w(
(r) can be defined (see
[72]
for a more detailed introduction). The first estimates of the two-point
correlation function go back to the seventies
[73],
but the lack of large redshift samples limited these early analyses
to the angular correlation function
w( ). This is
related to
). This is
related to  (r)
through the Limber equation
[72]
(r)
through the Limber equation
[72]

 is the radial selection
function expected for the 2D survey being analysed.
is the radial selection
function expected for the 2D survey being analysed.
 ) is well described by
a power law
) is well described by
a power law 
 -0.8, corresponding
to a spatial correlation function
(r /
r0)-
-0.8, corresponding
to a spatial correlation function
(r /
r0)- , with
r
, with
r  5
h-1 Mpc and
5
h-1 Mpc and

 - 1.8,
and a break with a rapid decline to zero around
r ~ 10 - 20 h-1 Mpc. As we shall discuss in the
following, modern surveys have significantly improved our knowledge of
the two-point correlation functions especially on scales
> 10 h-1 Mpc.
However, before discussing these most recent results, it is important
to briefly describe how galaxy peculiar velocities affect the
observed shape of
- 1.8,
and a break with a rapid decline to zero around
r ~ 10 - 20 h-1 Mpc. As we shall discuss in the
following, modern surveys have significantly improved our knowledge of
the two-point correlation functions especially on scales
> 10 h-1 Mpc.
However, before discussing these most recent results, it is important
to briefly describe how galaxy peculiar velocities affect the
observed shape of  (r) .
(r) .
 (s) from a power
law is complicated in the analysis of redshift surveys by the effects
induced by
galaxy peculiar velocities. Here s is now used to make it explicit
that separations are in reality not measured in true 3D space, but in
redshift space: what we actually measure when we take the
redshift of a galaxy is the quantity
cz = cztrue + vpec//,
where
vpec// is the component of the galaxy peculiar velocity
along the line of sight. This component, while typically
~ 100 km s-1 for ``field'' galaxies, can rise
above 1000 km s-1 in rich
clusters of galaxies. This distorts the real-space correlation
function in different ways, depending on the scale.
The resulting
(s) from a power
law is complicated in the analysis of redshift surveys by the effects
induced by
galaxy peculiar velocities. Here s is now used to make it explicit
that separations are in reality not measured in true 3D space, but in
redshift space: what we actually measure when we take the
redshift of a galaxy is the quantity
cz = cztrue + vpec//,
where
vpec// is the component of the galaxy peculiar velocity
along the line of sight. This component, while typically
~ 100 km s-1 for ``field'' galaxies, can rise
above 1000 km s-1 in rich
clusters of galaxies. This distorts the real-space correlation
function in different ways, depending on the scale.
The resulting  (s) ,
is in general flatter than the real-space
(s) ,
is in general flatter than the real-space
 (r) . This is
the result of two competing effects:
the small-scale pairwise velocity dispersion, mostly dominated by
high-velocity pairs in clusters of galaxies (i.e. those within
the so-called ``Fingers of God''), damps the amplitude of
(r) . This is
the result of two competing effects:
the small-scale pairwise velocity dispersion, mostly dominated by
high-velocity pairs in clusters of galaxies (i.e. those within
the so-called ``Fingers of God''), damps the amplitude of
 (r) below
~ 3 h-1 Mpc.
On the other hand, coherent flows towards large-scale structures
enhance the contrast of those structures lying perpendicularly to
the line of sight, thus amplifying
(r) below
~ 3 h-1 Mpc.
On the other hand, coherent flows towards large-scale structures
enhance the contrast of those structures lying perpendicularly to
the line of sight, thus amplifying
 (s) in the
linear regime (i.e.
above 10 - 20 h-1 Mpc). I will not enter here into
details on how
the wealth of information on the dynamics of galaxies contained in
these distortions can be extracted, but limit myself to a discussion
on how to correct them to recover the true shape of
(s) in the
linear regime (i.e.
above 10 - 20 h-1 Mpc). I will not enter here into
details on how
the wealth of information on the dynamics of galaxies contained in
these distortions can be extracted, but limit myself to a discussion
on how to correct them to recover the true shape of
 (r) . A more
complete discussion can be found, e.g., in
[74] and
[51].
(r) . A more
complete discussion can be found, e.g., in
[74] and
[51].
 (rp,
(rp,
 ) ,
where the separation vector s between two objects is split into two
components rp and
) ,
where the separation vector s between two objects is split into two
components rp and
 related as
s2 = rp2 +
related as
s2 = rp2 +
 2. This
two-dimensional correlation function can then be projected along the
line-of-sight direction, to obtain the function
2. This
two-dimensional correlation function can then be projected along the
line-of-sight direction, to obtain the function
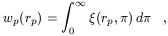
 (r) , as
e.g. the classical
(r) , as
e.g. the classical
 (r) = (r
/ r0)-
(r) = (r
/ r0)- [56],
or inverted through the Abel integral relations to recover the whole
[56],
or inverted through the Abel integral relations to recover the whole
 (r) .
(r) .
 ), where on the other
hand the strongest uncertainty in the
de-projection lies in the knowledge of the radial selection function.
), where on the other
hand the strongest uncertainty in the
de-projection lies in the knowledge of the radial selection function.
 (r)
The simple form observed from the first estimates of
w(
(r)
The simple form observed from the first estimates of
w( ) and
) and
 (r) at small
separations was consistent with the expectations of
gravitational growth from some initial spectrum of fluctuations (at
the time thought to possibly be a simple white-noise i.e.
(r) at small
separations was consistent with the expectations of
gravitational growth from some initial spectrum of fluctuations (at
the time thought to possibly be a simple white-noise i.e.
 k0, see
next section): as gravity has no
built-in preferential scale, a power law seemed to be a natural
consequence of gravitational clustering (see e.g.
[72]).
However, since then we have understood that plausible initial
conditions are all but a white-noise (see e.g. the first computation
of the linear power spectrum in a Universe dominated by Cold Dark Matter,
[76]),
so that the clustering we measure today with
k0, see
next section): as gravity has no
built-in preferential scale, a power law seemed to be a natural
consequence of gravitational clustering (see e.g.
[72]).
However, since then we have understood that plausible initial
conditions are all but a white-noise (see e.g. the first computation
of the linear power spectrum in a Universe dominated by Cold Dark Matter,
[76]),
so that the clustering we measure today with
 (r) is not just
the product of the nonlinear action of gravity.
(r) is not just
the product of the nonlinear action of gravity.
 (s) for
the ESP [77,
32],
the LCRS
[78], the
Stromlo-APM (Loveday et al. 1992b), and the Durham-UKST
[80]
surveys. These samples
represent a selection of data that should offer the best compromise
between depth and angular aperture, thus maximising the ability to
sample large scales. In addition, the dotted lines show a plot of
(s) for
the ESP [77,
32],
the LCRS
[78], the
Stromlo-APM (Loveday et al. 1992b), and the Durham-UKST
[80]
surveys. These samples
represent a selection of data that should offer the best compromise
between depth and angular aperture, thus maximising the ability to
sample large scales. In addition, the dotted lines show a plot of
 (r) obtained
through de-projection of the angular
w(
(r) obtained
through de-projection of the angular
w( ) from
the APM galaxy catalogue
[81]
under two different
assumptions about galaxy clustering evolution and thus selection function.
) from
the APM galaxy catalogue
[81]
under two different
assumptions about galaxy clustering evolution and thus selection function.

 (s) remains
positive to separations of 50 h-1 Mpc
or larger. Keeping in mind how the variance in galaxy counts is ~ 1
around 8 h-1 Mpc, we can conclude that a significant
range of scales
over which we measure positive clustering is still in the linear or
quasi-linear regime.
(s) remains
positive to separations of 50 h-1 Mpc
or larger. Keeping in mind how the variance in galaxy counts is ~ 1
around 8 h-1 Mpc, we can conclude that a significant
range of scales
over which we measure positive clustering is still in the linear or
quasi-linear regime.
 (r) , which is
in real space, while it is flatter
for all the redshift-space measures due to the suppression by
peculiar velocities discussed above.
Above ~ 5 h-1 Mpc there is unanimous evidence for
more power than
expected by a simple extrapolation of the small-scale slope. This
``bump'' or ``shoulder'' is evident both in the APM
(r) , which is
in real space, while it is flatter
for all the redshift-space measures due to the suppression by
peculiar velocities discussed above.
Above ~ 5 h-1 Mpc there is unanimous evidence for
more power than
expected by a simple extrapolation of the small-scale slope. This
``bump'' or ``shoulder'' is evident both in the APM
 (r) and in the
redshift-space measures, implying that it is not an effect of the
expected redshift-space amplification by coherent flows
[82].
We found clear early evidence for this excess when
studying clustering in the Perseus-Pisces survey
[47],
and realised that it was present already in the published CfA1 data
(as also noticed in
[83]).
At the time we suggested
that it was and indication for a steep power spectrum P(k)
(r) and in the
redshift-space measures, implying that it is not an effect of the
expected redshift-space amplification by coherent flows
[82].
We found clear early evidence for this excess when
studying clustering in the Perseus-Pisces survey
[47],
and realised that it was present already in the published CfA1 data
(as also noticed in
[83]).
At the time we suggested
that it was and indication for a steep power spectrum P(k)
 k-2.2 on
large scales. Further theoretical modeling
[84]
and the new direct
measures of P(k) in real space from the APM survey
[85],
confirmed that indeed there is a significant change in
k-2.2 on
large scales. Further theoretical modeling
[84]
and the new direct
measures of P(k) in real space from the APM survey
[85],
confirmed that indeed there is a significant change in
 (r)
around r
(r)
around r  3 - 5
h-1 Mpc. It was natural to interpret this as a
consequence of the transition between the strongly nonlinear
clustering regime at small separations, to a quasi-linear regime on
larger scales. In Section 5.3 we shall come back to
this point
while discussing directly the observed shape of P(k).
3 - 5
h-1 Mpc. It was natural to interpret this as a
consequence of the transition between the strongly nonlinear
clustering regime at small separations, to a quasi-linear regime on
larger scales. In Section 5.3 we shall come back to
this point
while discussing directly the observed shape of P(k).
 (s) for Abell clusters
[86]
showed that the cluster-cluster
correlation function is also well described by a power law, with a slope
apparently similar to that of galaxies, but a correlation length
about 4 times larger. In reality, due to the limited size of the
sample, the original fit was performed imposing a slope
(s) for Abell clusters
[86]
showed that the cluster-cluster
correlation function is also well described by a power law, with a slope
apparently similar to that of galaxies, but a correlation length
about 4 times larger. In reality, due to the limited size of the
sample, the original fit was performed imposing a slope
 = 1.8,
and therefore it was not really a measure of the functional shape of
cluster-cluster correlations.
Nevertheless, the fit was good enough, and it became generally accepted that
the cluster-cluster correlation function has a the same slope as galaxies,
= 1.8,
and therefore it was not really a measure of the functional shape of
cluster-cluster correlations.
Nevertheless, the fit was good enough, and it became generally accepted that
the cluster-cluster correlation function has a the same slope as galaxies,
 = 1.8, but larger
amplitude (see e.g.
[60]),
that is
= 1.8, but larger
amplitude (see e.g.
[60]),
that is
 cc(r)
cc(r)
 A .
A .
 gg(r).
In fact, this statement could
not rigorously be true if
a simple statistical amplification mechanism, as then suggested by
Kaiser [60],
were the origin of the different amplitude: clusters
trace scales > 10 h-1 Mpc, i.e. cover mostly
fluctuations that are in the
quasi-linear or linear regime, and it would have been a rather
strange conspiracy, that their slope were the same that galaxies
display on scales between 0.1 and 5 h-1 Mpc, where
clustering is highly nonlinear.
gg(r).
In fact, this statement could
not rigorously be true if
a simple statistical amplification mechanism, as then suggested by
Kaiser [60],
were the origin of the different amplitude: clusters
trace scales > 10 h-1 Mpc, i.e. cover mostly
fluctuations that are in the
quasi-linear or linear regime, and it would have been a rather
strange conspiracy, that their slope were the same that galaxies
display on scales between 0.1 and 5 h-1 Mpc, where
clustering is highly nonlinear.

 cc for X-ray
selected clusters
to that of galaxies, as we do in Figure 11
[91].
This figure shows a preliminary estimate of
cc for X-ray
selected clusters
to that of galaxies, as we do in Figure 11
[91].
This figure shows a preliminary estimate of
 cc from the
flux-limited REFLEX survey
[92],
compared to the galaxy-galaxy
correlation function from two volume-limited subsamples of the ESP
survey
[32]
(11) .
The dashed line on top of the cluster points is the Fourier
transform of the power spectrum of REFLEX clusters (computed
independently, see next section) while the bottom line has been
scaled down by an
arbitrary factor bcg2 = (3.3)2,
so as to overlap the galaxy
points. The agreement
between the shapes of the cluster and galaxy correlation functions is
remarkable. Here we also see how a proper functional description of
the shape is not just a simple power law. The one shown here is the
Fourier transform of the simple phenomenological shape for P(k)
suggested by Peacock
[51].
cc from the
flux-limited REFLEX survey
[92],
compared to the galaxy-galaxy
correlation function from two volume-limited subsamples of the ESP
survey
[32]
(11) .
The dashed line on top of the cluster points is the Fourier
transform of the power spectrum of REFLEX clusters (computed
independently, see next section) while the bottom line has been
scaled down by an
arbitrary factor bcg2 = (3.3)2,
so as to overlap the galaxy
points. The agreement
between the shapes of the cluster and galaxy correlation functions is
remarkable. Here we also see how a proper functional description of
the shape is not just a simple power law. The one shown here is the
Fourier transform of the simple phenomenological shape for P(k)
suggested by Peacock
[51].
 (r) and
the variance within a top-hat sphere of radius r
(r) and
the variance within a top-hat sphere of radius r

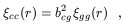

 50
h-1 Mpc, for more positive power on scales exceeding
100 h-1 Mpc.
50
h-1 Mpc, for more positive power on scales exceeding
100 h-1 Mpc.
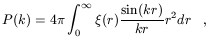
 /
/
 once we decompose the fluctuation field
once we decompose the fluctuation field
 =
=

 /
/
 over the Fourier basis
[51].
over the Fourier basis
[51].
 (r)
from redshift surveys, however, are affected in different ways by
uncertainties introduced, for example, by the poor knowledge of the
mean density (in which case the power spectrum is to be preferred),
or by the shape of the survey volume (whose effect is usually more
easily treated when computing
(r)
from redshift surveys, however, are affected in different ways by
uncertainties introduced, for example, by the poor knowledge of the
mean density (in which case the power spectrum is to be preferred),
or by the shape of the survey volume (whose effect is usually more
easily treated when computing
 (r) rather than
P(k)). Useful
references for learning more about this topic are
[94],
[7] and
[51],
where further
directions can be found to specific technical papers.
One practical benefit of the description of clustering in Fourier
space through P(k) is that for fluctuations of very
long spatial wavelength (
(r) rather than
P(k)). Useful
references for learning more about this topic are
[94],
[7] and
[51],
where further
directions can be found to specific technical papers.
One practical benefit of the description of clustering in Fourier
space through P(k) is that for fluctuations of very
long spatial wavelength ( > 100 h-1 Mpc), where
> 100 h-1 Mpc), where
 (r) is dangerously
close to zero and errors easily make the measured values fluctuate
around it, P(k) is on the contrary very large.
Around these scales, most models predict the power spectrum to have a
maximum, which reflects the size of the horizon at the epoch of
matter-radiation equivalence.
(r) is dangerously
close to zero and errors easily make the measured values fluctuate
around it, P(k) is on the contrary very large.
Around these scales, most models predict the power spectrum to have a
maximum, which reflects the size of the horizon at the epoch of
matter-radiation equivalence.
 k1, which is also
the kind of spectrum most naturally produced in inflationary scenarios
(see e.g.
[50]
for more details). In addition, k-modes in
Fourier space are statistically independent (a part from the
convolution effects due to the window function of the survey,
see below), and direct
k1, which is also
the kind of spectrum most naturally produced in inflationary scenarios
(see e.g.
[50]
for more details). In addition, k-modes in
Fourier space are statistically independent (a part from the
convolution effects due to the window function of the survey,
see below), and direct  2
comparisons to models is feasible,
which is in principle not the case when the correlation function is
analysed (see e.g.
[95]).
2
comparisons to models is feasible,
which is in principle not the case when the correlation function is
analysed (see e.g.
[95]).
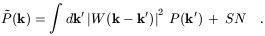
 solid
angle, this anisotropy brings contributions from different k's
into the same averaged k bin. It is important to keep these
limitations in mind when one compares estimates of P(k)
from different
surveys as we shall do here. A comprehensive discussion
on different estimators for P(k) and how to take these
effects into account can be found in
[102].
solid
angle, this anisotropy brings contributions from different k's
into the same averaged k bin. It is important to keep these
limitations in mind when one compares estimates of P(k)
from different
surveys as we shall do here. A comprehensive discussion
on different estimators for P(k) and how to take these
effects into account can be found in
[102].


 - 1.8. Below this scale,
P(k) steepens to
~ k-2, and this is what produces the excess power
in
- 1.8. Below this scale,
P(k) steepens to
~ k-2, and this is what produces the excess power
in  (s) on large
scales.
(s) on large
scales.
 (s) in the
CfA1 and Perseus-Pisces redshift surveys, and
confirms the early speculation that the observed change in slope of
(s) in the
CfA1 and Perseus-Pisces redshift surveys, and
confirms the early speculation that the observed change in slope of
 (r) is a
manifestation of the transition from the quasi-linear to the
strongly nonlinear clustering regime.
(r) is a
manifestation of the transition from the quasi-linear to the
strongly nonlinear clustering regime.
 0.05 h Mpc-1 is shown to be significant at
the 3
0.05 h Mpc-1 is shown to be significant at
the 3 level by a Karhunen-Loéve
[103]
Maximum Likelihood analysis
(14) .
The analysis of the whole survey
should also allow to put more serious constraints on the detailed
shape of P(k) around the turnover.
level by a Karhunen-Loéve
[103]
Maximum Likelihood analysis
(14) .
The analysis of the whole survey
should also allow to put more serious constraints on the detailed
shape of P(k) around the turnover.

 0.05 h
Mpc-1. Although their result was
questioned by other workers because of the possible incompleteness in
the sample and the way P(k) was estimated, the presence of such a
feature was confirmed by a more conservative reanalysis of Abell data
[111],
where a slightly less pronounced but still
significant peak is found, as we show in Figure 13.
The peak is indeed evident in the Abell data, while the preliminary
REFLEX sample is not yet able to put serious constraints on the shape
around the turnover. Note also the very good agreement of the slopes
of the three power spectra above
k
0.05 h
Mpc-1. Although their result was
questioned by other workers because of the possible incompleteness in
the sample and the way P(k) was estimated, the presence of such a
feature was confirmed by a more conservative reanalysis of Abell data
[111],
where a slightly less pronounced but still
significant peak is found, as we show in Figure 13.
The peak is indeed evident in the Abell data, while the preliminary
REFLEX sample is not yet able to put serious constraints on the shape
around the turnover. Note also the very good agreement of the slopes
of the three power spectra above
k  0.5 h
Mpc-1, and
at the same time the shift in amplitude of the three samples. The
latter is a clear manifestation, again, of the different bias of the
three samples. An X-ray selected sample as REFLEX allows for a more
direct link to the typical mass of the objects we are looking at (see
[115],
for a more extended discussion of these points).
0.5 h
Mpc-1, and
at the same time the shift in amplitude of the three samples. The
latter is a clear manifestation, again, of the different bias of the
three samples. An X-ray selected sample as REFLEX allows for a more
direct link to the typical mass of the objects we are looking at (see
[115],
for a more extended discussion of these points).
 (s) is very
coarse at these separations, there is a hint that
(s) is very
coarse at these separations, there is a hint that
 (s) becomes
positive again around
150 - 200 h-1 Mpc. This seems to be common to
nearly all surveys,
independently of their geometry (slice or 3D surveys), the kind of
tracer (galaxy or clusters), and the estimator used. As can be
readily seen by Fourier
transforming a ``standard'' P(k) (e.g., a CDM shape
[123]),
this damped oscillation of
(s) becomes
positive again around
150 - 200 h-1 Mpc. This seems to be common to
nearly all surveys,
independently of their geometry (slice or 3D surveys), the kind of
tracer (galaxy or clusters), and the estimator used. As can be
readily seen by Fourier
transforming a ``standard'' P(k) (e.g., a CDM shape
[123]),
this damped oscillation of
 (s) cannot be
reproduced if
P(k) has a smooth turnover around its maximum, and seems to be a
further hint for a sharp peak. A similar oscillation in the
correlation function was claimed for Abell clusters
[124],
and interpreted as evidence for a sharp feature in P(k).
(s) cannot be
reproduced if
P(k) has a smooth turnover around its maximum, and seems to be a
further hint for a sharp peak. A similar oscillation in the
correlation function was claimed for Abell clusters
[124],
and interpreted as evidence for a sharp feature in P(k).
 M and
M and

 :
48
:
48 M -
15
M -
15

 10.5, which for a flat Universe
(
10.5, which for a flat Universe
( M +
M +

 = 1), gives
= 1), gives
 M = 0.4 ± 0.1.
M = 0.4 ± 0.1.

 = 0.2). See
[125]
for details.
= 0.2). See
[125]
for details.
 b /
b /
 0
0
 0.3 or larger), and a rather
ad hoc combination of parameters (as e.g. a ``blue'' tilt of the
primordial spectrum) are required to match the observed Abell peak, while
at the same time being consistent with the cluster
abundance (15) .
More dramatically, it is worrying to see that no realistic CDM
parameter combination is capable to account for the excess power (the
``shoulder'') we were discussing in section 5.1, that is
displayed by virtually all modern surveys
[127].
0.3 or larger), and a rather
ad hoc combination of parameters (as e.g. a ``blue'' tilt of the
primordial spectrum) are required to match the observed Abell peak, while
at the same time being consistent with the cluster
abundance (15) .
More dramatically, it is worrying to see that no realistic CDM
parameter combination is capable to account for the excess power (the
``shoulder'') we were discussing in section 5.1, that is
displayed by virtually all modern surveys
[127].
 (s) .
Estimates of
(s) .
Estimates of
 (s) from whole
magnitude-limited surveys are
normally subject to weighting schemes, as e.g. the so-called J3
minimum-variance weighting, which, while allowing a better sampling
of very large scales, can affect the globale shape of
(s) from whole
magnitude-limited surveys are
normally subject to weighting schemes, as e.g. the so-called J3
minimum-variance weighting, which, while allowing a better sampling
of very large scales, can affect the globale shape of
 (s)
(Guzzo et al. 1999).
Volume-limited samples are much better defined in terms
of the properties of the galaxies they include, containing only
objects with luminosity above a well-defined threshold.
Back.
(s)
(Guzzo et al. 1999).
Volume-limited samples are much better defined in terms
of the properties of the galaxies they include, containing only
objects with luminosity above a well-defined threshold.
Back.