


1.3 Distribution Moments. The Mean and Variance
A probability distribution may be characterized by its moments. The rth moment of x about some fixed point x0 is defined as the expectation value of (x - x0)r where r is an integer. An analogy may be drawn here with the moments of a mass distribution in mechanics. In such a case, P(x) plays the role of the mass density.
In practice, only the first two moments are of importance. And, indeed, many problems are solved with only a knowledge of these two quantities. The most important is the first moment about zero,
This can be recognized as simply the mean or average of
x. If the
analogy with mass moments is made, the mean thus represents the
``center of mass'' of the probability distribution.
It is very important here to distinguish the mean as defined in
(Equation 8) from the mean which one calculates from a set of
repeated measurements. The first refers to the theoretical mean, as
calculated from the theoretical distribution, while the latter is an
experimental mean taken from a sample. As we shall see in
Sect. 4.2,
the sample mean is an estimate of the theoretical mean. Throughout the
remainder of this chapter, we shall always use the Greek letter
µ todesignate the theoretical mean.
The second characteristic quantity is the second moment about the mean
(also known as the second central moment),
This is commonly called the variance and is denoted as
Further moments, of course, may also be calculated, such as the
third moment about the mean. This is known as the skewness and it
gives a measure of the distribution's symmetry or asymmetry. It is
employed on rare occasions, but very little information is generally
gained from this moment or any of the following ones.
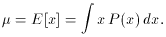
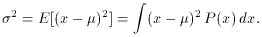
 2. The square
root of the variance,
2. The square
root of the variance,  , is
known as the standard deviation. As can be
seen from (9), the variance is the average squared deviation of x
from the mean. The standard deviation,
, is
known as the standard deviation. As can be
seen from (9), the variance is the average squared deviation of x
from the mean. The standard deviation,  , thus measures the dispersion
or width of the distribution and gives us an idea of how much the
random variable x fluctuates about its mean. Like µ,
(9) is the
theoretical variance and should be distinguished from the sample
variance to be discussed in Section 4.
, thus measures the dispersion
or width of the distribution and gives us an idea of how much the
random variable x fluctuates about its mean. Like µ,
(9) is the
theoretical variance and should be distinguished from the sample
variance to be discussed in Section 4.