


1.4 The Covariance
Thus far we have only considered the simple case of single variable probability distributions. In the more general case, the outcomes of a process may be characterized by several random variables, x, y, z..... The process is then described by a multivariate distribution P(x, y, z, . . .). An example is a playing card which is described by two variables: its denomination and its suit.
For multivariate distributions, the mean and variance of each separate random variable x, y,... are defined in the same way as before (except that the integration is over all variables). In addition a third important quantity must be defined:
where µx, and µy are the
means of x and y respectively. Equation (10)
is known as the covariance of x and y and it is
defined for each pair of
variables in the probability density. Thus, if we have a trivariate
distribution P(x, y, z), there are three covariances: cov(x,
y), cov(x, z) and cov(y, z).
The covariance is a measure of the linear correlation between the two
variables. This is more often expressed as the correlation coefficient
which is defined as
where
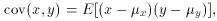
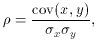
 x and
x and
 y are the standard
deviations of x and y. The
correlation coefficient varies between -1 and +1 where the sign
indicates the sense of the correlation. If the variables are perfectly
correlated linearly, then
|
y are the standard
deviations of x and y. The
correlation coefficient varies between -1 and +1 where the sign
indicates the sense of the correlation. If the variables are perfectly
correlated linearly, then
| | = 1. If the
variables are independent (1)
then
| = 1. If the
variables are independent (1)
then  = 0. Care must
be taken with the converse of this last
statement, however. If
= 0. Care must
be taken with the converse of this last
statement, however. If  is found to be 0, then x and y can only be
said to be linearly independent. It can be shown, in fact, that if x
and y are related parabolically, (e.g., y =
x2), then
is found to be 0, then x and y can only be
said to be linearly independent. It can be shown, in fact, that if x
and y are related parabolically, (e.g., y =
x2), then
 = 0.
= 0.
1 The mathematical definition of
independence is that the
joint probability is a separable function, i.e., P(x, y) =
P1(x) P2(y)