2.1 The Binomial Distribution
Many problems involve repeated, independent trials of a process in which the outcome of a single trial is dichotomous, for example, yes or no, heads or tails, hit or miss, etc. Examples are the tossing of a coin N times, the number of boys born to a group of N expectant mothers, or the number of hits scored after randomly throwing N balls at a small, fixed target.
More generally, let us designate the two possible outcomes as success and failure. We would then like to know the probability of r successes (or failures) in N tries regardless of the order in which they occur. If we assume that the probability of success does not change from one trial to the next, then this probability is given by the binomial distribution,
where p is the probability of success in a single trial.
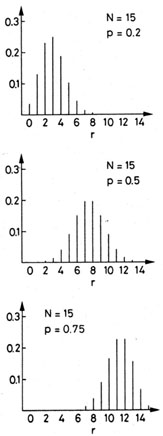
Equation (12) is a discrete distribution and Fig. 1 shows its form for various values of N and p. Using (8) and (9), the mean and variance many be calculated to yield
|
Fig. 1. Binomial distribution for various values of N and p. |
It can be shown that (12) is normalized by summing P(r) from r = 0 to r = N. Here it will be noticed that P(r) is nothing but the rth term of the binomial expansion (whence the name!), so that
Finding the cumulative distribution between limits other than 0 and N is somewhat more complicated, however, as no analytic form for the sum of terms exist. If there are not too many, the individual terms may be calculated separately and then summed. Otherwise, tabulations of the cumulative binomial distribution may be used.
In the limit of large N and not too small p, the binomial
distribution may be approximated by a Gaussian distribution with mean
and variance given by (13) and (14). For practical calculations,
using a Gaussian is usually a good approximation when N is greater
than about 30 and p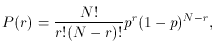 
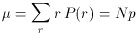
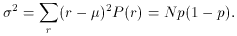
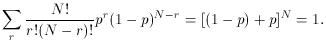
0.05. It is necessary, of course, to ignore the
discrete character of the binomial distribution when using this
approximation (although there are corrections for this). If p is small
( 0.05), such that the product
Np is finite, then the binomial
distribution is approximated by the Poisson distribution discussed in
the next section.