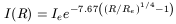
| (24) |



a) From the stellar velocity dispersion.
b) From the neutral gas velocities found in the outermost region, in certain galaxies.
c) From the X-ray corona surrounding all ellipticals.
There also exist complementary methods, using observations of ionized gas in the central parts, globular clusters, gravitational lensing, theoretical considerations about the bar instability and the chemical evolution.
The general conclusion, taking into account all these studies, could be, in summary, that dark matter amounts comparable to visible matter could be present in the visible part of the galaxy, and that larger dark matter amounts, probably as large as in spirals, are present in a halo surrounding the galaxy, but that, in any case, the evidence of dark matter in ellipticals is less than in the case of spirals. Even the complete absence of dark matter cannot be easily ruled out.
Several reviews have been written on the topic (e.g. Ashman, 1992; Trimble, 1987; de Zeeuw, 1992; Kent, 1990; Bertin and Stavielli, 1993). Let us remember that the surface brightness of an elliptical galaxy can be fitted by de Vaucouleurs' law
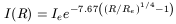
| (24) |
(de Vaucouleurs, 1948), where Re is the radius enclosing half of the light and Ie = I(R = Re) is another constant. The value of Re is often used as a parameter that normalizes all lengths as does the radial scale length in spirals. This law seems to be rather well matched, but it is just one fitting which might be less appropriate for some subtypes (Andreakis, Peletier and Balcells, 1995).
Let us comment on the three basic methods, and more briefly about other methods:
a) The observations of stellar velocity dispersion, interpreted in terms of Jeans' equation or of the Virial theorem, can provide the total mass for R < Re, or even at larger distances.
The Virial theorem for a spherical, steady-state, static isothermal elliptical galaxy reduces to the simple expression
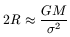
| (25) |
where R is an equivalent radius. For a given R,
![]()
![]() M, because the stellar chaotic thermal velocities, quantified by the
velocity dispersion,
M, because the stellar chaotic thermal velocities, quantified by the
velocity dispersion, ![]() , must prevent gravitational collapse.
The larger the mass, the larger the stellar velocities must be. This
formula gives a first approximate mass. In practice
however, much more sophisticated models than this one are used to
interpret the
velocity dispersions. There is a "degeneracy" between the unknown
anisotropy and the unknown gravitational potential. If the anisotropy
of the orbits is known the potential can be determined, but not both
simultaneously. We should know if orbits are mainly circular, or
mainly radial, or something in between. The anisotropy is
characterized by the parameter
, must prevent gravitational collapse.
The larger the mass, the larger the stellar velocities must be. This
formula gives a first approximate mass. In practice
however, much more sophisticated models than this one are used to
interpret the
velocity dispersions. There is a "degeneracy" between the unknown
anisotropy and the unknown gravitational potential. If the anisotropy
of the orbits is known the potential can be determined, but not both
simultaneously. We should know if orbits are mainly circular, or
mainly radial, or something in between. The anisotropy is
characterized by the parameter ![]() , which is defined later, in
Section 3.5.2.
, which is defined later, in
Section 3.5.2.
Pioneering works by Binney, Davies and Illingworth (1990), van der Marel, Binney and Davies (1990) and others have concluded that no gradients in M/L were clearly appreciated and that no dark matter was needed to explain the central surface brightness and the velocity dispersions. The M/L values are of the order of 12h (Binney and Tremaine, 1987) (about 8 for h=0.65) which is comparable to the solar neighbourhood values. It is slightly higher, but this fact can be explained mainly by the absence of young stars in ellipticals. One-component models, without any halo, provide a good zeroth-order description (Bertin, Saglia and Stiavelli, 1992).
Bertin, Saglia and Stiavelli (1992) also considered two-component spherically symmetric collisionless self-consistent models, which were later used to interpret real data from 10 bright selected galaxies (Saglia, Bertin and Stiavelli, 1992) and found some evidence for dark matter to be of the order of the visible mass. The presence of rotation and of tangential anisotropy makes it difficult to draw firm conclusions.
As in the case of spirals
with their rotation curve, a flat or slowly increasing velocity dispersion,
![]() (r), may indicate dark halos dominating the
dynamics
(Saglia et al. 1993)
but there is a surprisingly large variety of
(r), may indicate dark halos dominating the
dynamics
(Saglia et al. 1993)
but there is a surprisingly large variety of ![]() -profiles,
some of which decrease outwards relatively fast. Therefore, Saglia
et al. did not find any compelling evidence of dark matter out to 1-2
Re.
Carollo et al. (1995)
observed flat or gently declining velocity dispersion
profiles in four elliptical galaxies, concluding that massive dark halos
must be
present in three of the four galaxies, although no clear conclusion was
obtained for the fourth.
Bertin et al. (1994)
found that in a sample of 6 galaxies,
three of them were not suitable for reliable modelling, two of them
presented no evidence for dark matter and one
(NGC 7796) appeared to
have a distinct
dark halo. But the conclusion that some galaxies have a dark halo
while others do not is problematic for understanding what an elliptical
galaxy is.
De Paolis, Ingrosso and
Strafella (1995)
found that dark matter
inside Re is negligible with respect to the visible mass.
-profiles,
some of which decrease outwards relatively fast. Therefore, Saglia
et al. did not find any compelling evidence of dark matter out to 1-2
Re.
Carollo et al. (1995)
observed flat or gently declining velocity dispersion
profiles in four elliptical galaxies, concluding that massive dark halos
must be
present in three of the four galaxies, although no clear conclusion was
obtained for the fourth.
Bertin et al. (1994)
found that in a sample of 6 galaxies,
three of them were not suitable for reliable modelling, two of them
presented no evidence for dark matter and one
(NGC 7796) appeared to
have a distinct
dark halo. But the conclusion that some galaxies have a dark halo
while others do not is problematic for understanding what an elliptical
galaxy is.
De Paolis, Ingrosso and
Strafella (1995)
found that dark matter
inside Re is negligible with respect to the visible mass.
b) A small fraction of elliptical galaxies are surrounded by a ring of
neutral hydrogen, for instance, NGC 1052, NGC 4278 and NGC 5128. In
these cases, the determination of a dark matter halo is very
similar to its determination in spiral galaxies, from the rotation
curve. One of the best studied gaseous rings is that of IC 2006
(Schweizer, van Gorkom and
Seitzer, 1989).
The neutral gas counter-rotates at a
radius of 18.9 kpc (6.5 Re) and has a total mass of
4.8 × 108M![]() . This galaxy also has a counter-rotating central mass of
ionized gas out to
. This galaxy also has a counter-rotating central mass of
ionized gas out to ![]() 5 kpc. These gaseous components of some ellipticals
have either been accreted or are the remnant of a merger from which the
elliptical was created.
5 kpc. These gaseous components of some ellipticals
have either been accreted or are the remnant of a merger from which the
elliptical was created.
Schweizer, van Gorkom and
Seitzer (1989)
found evidence for a DM halo in
IC 2006 with twice the mass of the luminous matter
within 6.5
Re,
under the assumption that the HI ring is flat and circular.
Bertola et al. (1993)
analyzed five elliptical galaxies, combining the M/L ratios obtained
with the inner ionized hydrogen component and the outer neutral hydrogen
ring. M/L is constant out to about Re with a moderate
value of
3.5![]() 0.9
but becomes very large in the ring region. These authors found a similarity
in the distribution of dark matter in ellipticals and in spirals, suggesting
a similar picture for the origin of both.
0.9
but becomes very large in the ring region. These authors found a similarity
in the distribution of dark matter in ellipticals and in spirals, suggesting
a similar picture for the origin of both.
As we will discuss later, magnetic fields may explain rotation curves without requiring dark matter in spirals. Similar arguments can be considered to interpret gaseous rings around ellipticals. In particular, a narrow ring is pushed towards the centre more easily than a disk, because the outward magnetic pressure force need not be compensated by a magnetic tension. It is to be emphasized that the IC 2006 gaseous ring is very narrow, and is not even resolved by VLA.
c) The most promising method to study dark matter in ellipticals is based
on the existence of X-ray halos. A hot X-ray emitting gas typically extends
out to 50 kpc
(Forman, Jones and Tucker
1985).
The probable origin of the gas is mass
loss from stars; supernovae heat it up to
![]() 107K,
bremsstrahlung being the main cooling process
(Binney and Tremaine, 1987).
Typical masses of this hot gas are
1010M
107K,
bremsstrahlung being the main cooling process
(Binney and Tremaine, 1987).
Typical masses of this hot gas are
1010M![]() .
.
Hydrostatic equilibrium is usually assumed for the gas. Then, for a spherical DM halo
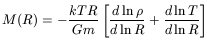
| (26) |
where ![]() is the density of the gas. Once M(R) is determined in
this way, we obtain the DM halo profile.
is the density of the gas. Once M(R) is determined in
this way, we obtain the DM halo profile.
The gas is not in perfect hydrostatic equilibrium. The innermost gas in the X-ray halo is more efficiently cooled, because cooling is proportional to the electron density, which is still high. An inwards flow in the inner region is therefore to be expected (Binney and Tremaine, 1987). Cooling flows have been observed (Mushotzky et al. 1994) and models including radial flows have been developed (e.g. Ciotti et al. 1991). The equilibrium probably breaks down in galaxies with low X-ray-to-optical luminosity ratios. Nevertheless, hydrostatic equilibrium is generally assumed.
In the above formula, the temperature profile T(R) is not
provided
by the observations with enough precision. The strengths of some X-ray
lines or the shape of the X-ray continuum should provide this
T-profile but, in practice, this is still rather problematic. For giant
cD galaxies, like M87, the temperature is exceptionally well
determined and the method provides more reliable results. For M87 the
data are spectacular:
M(R < 300kpc) ![]() 3 × 1013M
3 × 1013M![]() ;
the mass-to-light ratio reaches a value of 750; about 95% of M87 mass
is dark matter
(Fabricant and Gorenstein, 1983; Stewart et al. 1984;
Binney and Cowie, 1981).
However, cD galaxies may be exceptional; as
they lie at the centre of a rich cluster, the DM encountered could
belong to the cluster as a whole. Below, we address this problem in
Section 5.
;
the mass-to-light ratio reaches a value of 750; about 95% of M87 mass
is dark matter
(Fabricant and Gorenstein, 1983; Stewart et al. 1984;
Binney and Cowie, 1981).
However, cD galaxies may be exceptional; as
they lie at the centre of a rich cluster, the DM encountered could
belong to the cluster as a whole. Below, we address this problem in
Section 5.
Difficulties arise in the analysis of normal ellipticals. If T(r) is unknown, it is tempting to assume an isothermal distribution (e.g. Forman, Jones and Tucker, 1985), which might be justifiable. Mushotzky et al. (1994) were able to obtain 6 points of T(R) in NGC 4636, finding that T was approximately constant. Moreover Matsushita (1997) and Jones and Forman (1994) confirmed the constancy of T(R). High M/L ratios are in general obtained, in the range 10-80, especially at large distances, but Trinchieri, Fabbiano and Canizares (1986) concluded that DM halos were not absolutely required by the data. Fabbiano (1989) also found much lower masses.
Furthermore, the contribution of unresolved discrete X-ray sources, such as accreting binaries, complicates the analysis (de Paolis, Ingrosso and Strafella, 1995), which could be related to the fact that the relative amount of DM is higher for X-ray bright ellipticals.
Models often take as a boundary condition that X-ray emitting gas is confined by the cluster intergalactic gaseous pressure (Fabian et al. 1986). Other authors assume a vanishing pressure at infinity (Loewenstein and White, 1999).
The gas responsible for the X-ray emission cannot rotate very fast and
hence no dynamo can generate magnetic fields capable of affecting the
hydrostatic equilibrium. However, intergalactic magnetic fields could
have an influence as a boundary condition. For the intracluster
intergalactic space, with
n ![]() 10-5cm-3 and
T
10-5cm-3 and
T ![]() 107K
the thermal pressure is of the order of
10-14dyncm-2. As
discussed below, cluster intergalactic fields are of the order of
10-6 G, and therefore the magnetic energy density is of the
order of
the thermal pressure. External magnetic fields could contribute to
confining the X-ray emanating hot gas, thus reducing the large amounts
of dark matter required. This external field would not act
isotropically and would produce eccentric X-ray isophotes, such as for
instance in NGC 720.
Eilek (1999)
makes suggestions about the
importance of magnetic fields in the dynamics of clusters which are
relevant to the dynamics of X-ray halos around giant ellipticals at
the centre of clusters, where the field can provide an important part
of the pressure support.
107K
the thermal pressure is of the order of
10-14dyncm-2. As
discussed below, cluster intergalactic fields are of the order of
10-6 G, and therefore the magnetic energy density is of the
order of
the thermal pressure. External magnetic fields could contribute to
confining the X-ray emanating hot gas, thus reducing the large amounts
of dark matter required. This external field would not act
isotropically and would produce eccentric X-ray isophotes, such as for
instance in NGC 720.
Eilek (1999)
makes suggestions about the
importance of magnetic fields in the dynamics of clusters which are
relevant to the dynamics of X-ray halos around giant ellipticals at
the centre of clusters, where the field can provide an important part
of the pressure support.
Buote and Canizares (1998) observed a different isophote geometry for X-rays and for the optical in NGC 720. The X-ray isophotes are more elongated and their major axes are misaligned by about 30o. If the total matter were distributed as is the optical light, it could not produce the observed ellipticities of the X-ray isophotes. They interpreted this ellipticity as being produced by a dark matter halo and developed a model that did not need the T(R) profile, and which also favoured the existence of a large dark matter halo. Davis and White (1996) and Loewenstein and White (1999), too, developed methods not requiring the temperature profile that imply DM halos.
d) In addition to these basic methods there are others that should be mentioned. The image splitting of an individual gravitational lens system consisting of an elliptical is only slightly sensitive to the existence of a DM halo, and so, one cannot definitely discriminate between galaxies with and without halos, with some exceptions (Breimer and Sanders, 1993; Kochanek, 1995). Indeed, in three cases where the lens is clearly a single galaxy, there is no need to consider any dark matter halo. Maoz and Rix (1993), however, deduce from gravitational lensing methods that M(R) increases linearly with R, as is typical in isothermal halos.
Globular clusters have been considered to deduce the existence of dark matter halos in ellipticals, mainly in M87 (Huchra and Brodie, 1987; Mould et al., 1990). They support the conclusions obtained by other methods: models without dark halos do not fit the data in M87, but they cannot be excluded in NGC 4472 (Mould et al. 1990). This problem is considered in Section 2.6. Planetary nebulae have also been considered in NGC 5128 by Ford et al. (1989) and by others, who found a radial increase in (M/LB) reaching values of about 10, although de Zeeuw (1992) suggested a lower gradient. Ciardullo and Jacoby (1993) deduced that the non-interacting elliptical galaxy NGC 3379 has no dark matter halo, and that a constant M/L of about 7 explained the observations perfectly. Theoretical studies of bar instability (Stiavelli and Sparke 1991) and chemical evolution (Matteuci 1992) were unable to unambiguously determine the presence of a dark halo.
In conclusion, elliptical galaxies could have dark matter halos similar in mass and extent to those in spiral galaxies (Danziger, 1997), but the evidence is not so clear and it cannot even be completely rejected that they possess no dark halo at all. As exceptions, in giant cD galaxies like M87, the existence of large amounts of dark matter seems to be fully demonstrated.