3.5.2 Statistics of binary galaxies

It is tempting to observe binary galaxies to obtain galactic masses. Typical periods are, however, so large that orbits cannot be observed. On the other hand, typical distances between the two galaxies are much larger than visible galactic sizes, and therefore we could, in principle, obtain total masses.

The observations permit the obtention of "projected distances", $\Delta$r, and of "differences in the velocity component along the line-of-sight", $\Delta$v. From both series of data we must infer a mean M/L ratio. The analysis must be statistical as no parameter of the individual orbits is known.

The first problem to resolve, and a very serious one, is the selection of a suitable sample. Chance superpositions must be avoided: including in the sample two unbounded galaxies, for which the velocity difference is due to Hubble's flow, could give a very high $\Delta$v and hence an overestimation of the mean mass. If the pair is not isolated, the influence of a third galaxy could produce a misinterpretation of the results; galaxies are often in small or large clusters and are rarely found in truly isolated pairs.

Usually, only pairs with a projected separation of less than a given value, R, are accepted in the sample. Binney and Tremaine (1987) have warned of this danger. Suppose that we take R as smaller than the mean true pair distance. Then, the velocity should be mainly perpendicular to the line-of-sight, and therefore much greater than the projected velocity along the line of sight; then $\Delta$v would be underestimated, as would the galactic masses.

Limit values of $\Delta$r and of $\Delta$v become necessary, but then, we find the results that we expect. Indeed, Sharp (1990) after comparing the large discrepancies between different workers, even with similar samples, was very pessimistic about the ability of these statistical approaches to derive galactic masses.

To interpret statistical distributions of $\Delta$r and $\Delta$v in order to obtain M, the mass of the two galaxies, it is necessary to adopt a law for the distribution of the true separation r; for example, $\varphi$(r) $\propto$ r^{- $\gamma$}, deduced with the two-point correlation function of galaxies (Peebles, 1974). Observations indicate that $\gamma$ $\sim$ 1.8. This distribution might not be valid for close binary systems. It is also necessary to adopt a hypothesis about the orbits, and more precisely about the value of the parameter $\beta$, defined as

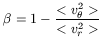
(63)

where v_$\theta$ and v_r are the azimuthal and radial components of the velocity. If the orbits are radial, < v_$\theta$² > = 0 and we should take $\beta$ = 1. If the orbits are perfectly circular, then < v_r² > = 0 and $\beta$ = - $\infty$. An interesting intermediate assumption is the condition of isotropy < v_r² > = < v_$\theta$² >, hence $\beta$ = 0.

A natural way to study binary samples is the adoption of galaxies as mass points. In a classical analysis by White et al. (1983), however, it was demonstrated that the mass point model does not fit the data. This model predicts a correlation between $\Delta$v and $\Delta$r (clearly ($\Delta$v)² should correlate with ($\Delta$r)^-1), which is not found. This negative result is highly interesting, as it can be interpreted as being due to the existence of greatly extended halos. If the force, instead of - GM/r², were of the type $\propto$ r^-1, the correlation [($\Delta$v)² $\leftrightarrow$ ($\Delta$r)^-1] would not exist.

This classical paper also claimed other evidence favouring the existence of massive extended halos. They found dark-to-luminous mass ratios higher than those found with rotation curves. This is really to be expected, because mass determinations from rotation curves are made at a maximum radius lower than the rim of the halo, while a companion could be far away, at a distance greater than the sum of both halos. Indeed their results are compatible with extrapolations of observed rotation curves. These authors found a relation of the type M/L $\propto$ L^-3/4. Therefore, low luminosity galaxies should contain large amounts of dark matter. Lake and Schommer (1984) confirmed very high M/L values in a sample of dwarf irregular pairs.

However, Karachentsev (1983, 1985) found no evidence of dark matter in binary systems, using very large samples, even containing some galaxies with well observed flat rotation curves.

Honma (1999) found M/L for spiral pairs in the range 12-16, lower than M/L for ellipticals, confirming previous results by Schweizer (1987). These values are clearly lower than those previously reported.

Among the large list of workers who have attempted to obtain proof of dark matter with this method, noticeable are the studies by van Moorsel (1987), Charlton and Salpeter (1991) and others, favouring the scenario of a large common dark matter envelope, as we have seen in the pair formed by M31 and the Milky Way. From the cosmological point of view, whether dark matter lies in individual or in common halos is unimportant, but from the point of view of galactic structure and evolution, the two models are completely different.

As stated by Binney and Tremaine (1987) "the mass-to-light ratio of binary galaxies is probably large, but not so large as the ratio of the mass of papers on this subject to the light they have shed on it". Even the concept of binary systems is controversial: with typical velocities of 100 kms^-1 and separations of 100 kpc, a typical value for the orbital period is of the order of Hubble's time. In most cases, such as in the M31-Milky Way pair, a simple orbit has not been completed. The Universe is expanding with a typical time of the orbital period. Nevertheless, despite the large variety of results, it should be emphasized that the most widely accepted point of view is that binary galaxies possess large amounts of dark matter, either in individual halos or in common super halos.