


The Local Group contains more than 35 galaxies, most of which are dwarf ellipticals and irregulars with low mass; this complicated system may be considered as being formed by two main galaxies, M31 and the Milky Way, with other dynamically less important satellites belonging either to one of them or to the pair.
This picture is derived from
galactic luminosities, but when possible dark matter is taken into
account, it
is not clear at all. M31 has a visible mass of about
4 × 1011M![]() . The Milky Way,
1011M
. The Milky Way,
1011M![]() . Next are M33 with
4 × 1010M
. Next are M33 with
4 × 1010M![]() , LMC with about
2.3 × 1010M
, LMC with about
2.3 × 1010M![]() ,
SMC with
6.3 × 109M
,
SMC with
6.3 × 109M![]() , IC10 with
3 × 109M
, IC10 with
3 × 109M![]() and other minor members. Note that this list, when
ordered following the total mass, could be changed. For instance, LMC
has a visible mass of
and other minor members. Note that this list, when
ordered following the total mass, could be changed. For instance, LMC
has a visible mass of ![]() 1/5 the mass of the Milky Way. As it has been
suggested that irregulars may
contain more dark matter than bright galaxies, the
total mass of LMC could be as large as, or even more massive than,
that of the
Milky Way. In this case it could no longer be considered our
"satellite". Let us however retain the more standard viewpoint
and consider that M31 and the Milky Way are dynamically dominant and
form a binary system.
1/5 the mass of the Milky Way. As it has been
suggested that irregulars may
contain more dark matter than bright galaxies, the
total mass of LMC could be as large as, or even more massive than,
that of the
Milky Way. In this case it could no longer be considered our
"satellite". Let us however retain the more standard viewpoint
and consider that M31 and the Milky Way are dynamically dominant and
form a binary system.
M31 has a line-of sight velocity of ![]() -300 km s-1, and therefore
it is approaching us. Taking into account our motion of rotation
within the galaxy of about
220kms-1, it is easy to deduce that
the speed of M31 with respect to the centre of our Galaxy is about
-125kms-1. Both galaxies are approaching one another,
with M31 therefore being
an exception in the general motion of expansion of the
Universe. There are different interpretations of this fact:
-300 km s-1, and therefore
it is approaching us. Taking into account our motion of rotation
within the galaxy of about
220kms-1, it is easy to deduce that
the speed of M31 with respect to the centre of our Galaxy is about
-125kms-1. Both galaxies are approaching one another,
with M31 therefore being
an exception in the general motion of expansion of the
Universe. There are different interpretations of this fact:
a) "Ships passing in the night"
Besides the expansion velocity following Hubble's law, galaxies have a peculiar velocity. For instance, our galaxy is moving with respect to the CMB black body at about 620kms-1. Within a cluster, peculiar motions are also of the order of 600kms-1. Even if these high velocities could be interpreted in other ways, such as bulk motions of large inhomogeneities or only characteristic of rich clusters, it is evident that some thermal-like peculiar velocities of this order of magnitude characterize the velocity dispersion of present galaxies, once the Hubble flow is subtracted. If we write for the velocity of a galaxy
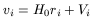
| (30) |
where Vi is independent of ri, for distances less than V/H0, Hubble's law becomes imprecise and of little use, peculiar velocities being larger than expansion velocities. The law is imprecise for distances shorter than about 10 Mpc and becomes absolutely unsuitable for r<1 Mpc. Therefore, a simple interpretation for the approaching motion of M31 is that it is due to pure initial conditions, and is unrelated to the mass of the Local Group.
Van der Bergh suggested that our Galaxy and M31 might not form any coherent system, and that both galaxies "were passing each other as ships pass in the night" (Lynden-Bell, 1983).
b) The "timing" argument of Kahn and Woltjer.
The most widely accepted interpretation of the negative velocity of M31 was
first given by
Kahn and Woltjer (1959).
They assumed that this double
system has negative energy, i.e. it is held together by
gravitational forces. However, considering visible matter only, they
estimated the kinetic energy of the system to be about
1.25 × 1058 erg, and the gravitational energy
-6 × 1057
erg. Even with an apparent positive energy (unbounded system) they
considered the possibility of large quantities of intergalactic
material in the form of gas, which would render the total energy
negative. This gaseous intergalactic mass was not confirmed by later
observations. Instead, today, the argument of Kahn and Woltjer is
considered as a proof for either the existence of large dark matter
halos surrounding M31 and the Milky Way or (at least) a large common
DM super halo pervading the Local Group. They deduced, with a simple
order of magnitude argument, that the effective mass was larger than
1.8 × 1012M![]() , about six times larger than the reduced
mass of M31 and the Milky Way.
Lynden-Bell (1983)
has presented a more precise description.
, about six times larger than the reduced
mass of M31 and the Milky Way.
Lynden-Bell (1983)
has presented a more precise description.
It is interesting to note, also in this historic paper, that Kahn and Woltjer (1959) considered that the ram pressure produced by this hypothetical intergalactic gas, due to the motion of both galaxies with respect to it, was responsible for warps of both galaxies. This hypothesis for the origin of warps has today been largely forgotten, but it could explain the coherence in the orientation of the warps of M31, M33 and the Milky Way shown by Zurita and Battaner (1997). This coherence can only be explained by the hypothesis of Kahn and Woltjer and by the magnetic hypothesis (Battaner, Florido and Sanchez-Saavedra, 1990, 1991; Battaner, 1995; Battaner, Florido, 1997; Battaner and Jimenez-Vicente, 1998; Battaner et al. 1991; see also Binney, 1991, and Kuijken, 1997).
Coming back to the "timing" argument, let us obtain a similar order of magnitude, by an argument closer to that presented by Lynden-Bell (1983). Suppose that the pregalaxies later to become M31 and the Milky Way were formed at Recombination. Inhomogeneity seeds were previously developed, but at Recombination, photon decoupling allowed matter to freely collapse. Identifying Recombination as the epoch of the Local Group birth, at about 106 years after the Big Bang, is equivalent to this birth being produced at the very beginning of the Universe, as 106 years is negligible when compared with 14 Gyr, at present.
Then the Universe was much smoother, so we can assume a vanishing initial transverse velocity. The Local Group, i.e. the two galaxies, were born so close to each other that gravitation was stronger than the expansion effect, so that we assume that during the period of the birth of both galaxies, there was a negligible relative velocity between them, in the line connecting them. Therefore, we assume that 14 Gyr ago, both galaxies were at rest with respect to each other, and since then their mutual gravitational attraction has reduced their separation and is responsible for the 125 kms-1 approaching velocity observed today.
The general equations for the orbit in the framework of Newtonian Mechanics adopt the following parametric form
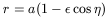
| (31) |
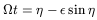
| (32) |
where r is the mutual distance, t the time and ![]() the
eccentricity, while
the
eccentricity, while ![]() and a are constants. The parameter
and a are constants. The parameter ![]() is
called the eccentric anomaly. The sum of the masses of both galaxies,
M, is related to these constants, through
is
called the eccentric anomaly. The sum of the masses of both galaxies,
M, is related to these constants, through
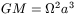
| (33) |
If ![]() were zero, we would have r = a
(constant) and
were zero, we would have r = a
(constant) and
![]() =
= ![]() t, e.g. a circular orbit with a constant
velocity. But given
that our initial transverse velocity was assumed to be null, our orbit
cannot be circular, but rather, it will become approximately a
straight line. We thus consider
t, e.g. a circular orbit with a constant
velocity. But given
that our initial transverse velocity was assumed to be null, our orbit
cannot be circular, but rather, it will become approximately a
straight line. We thus consider
![]() = 1.
= 1.
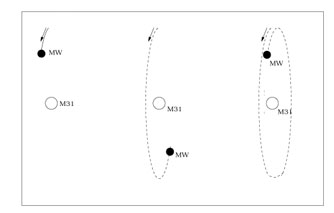
|
Figure 13. Different possibilities to understand the negative radial velocity of M31. |
Figure 13 presents various possibilities:
the first possibility provides the lowest mass and we will concentrate on this one. We have
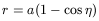
| (34) |
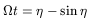
| (35) |
therefore
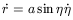
| (36) |
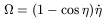
| (37) |
At the birth (approximately, at the Big Bang) we set t =
t1. Then,
![]() = 0, as we have assumed.
= 0, as we have assumed.
![]()
![]() 0, always, as
otherwise (37) would imply
0, always, as
otherwise (37) would imply ![]() = 0. Therefore,
sin
= 0. Therefore,
sin![]() = 0,
which gives either
= 0,
which gives either ![]() = 0 or
= 0 or
![]() =
= ![]() . But
. But ![]() = 0
would imply r1 = 0, while we have started with the
distance of
the galaxies being a maximum (2a). Therefore,
= 0
would imply r1 = 0, while we have started with the
distance of
the galaxies being a maximum (2a). Therefore,
![]() =
= ![]() . Hence, r1 = 2a (as expected),
. Hence, r1 = 2a (as expected),
![]() t1 =
t1 = ![]() ,
,
![]() = 0,
= 0,
![]() = 2
= 2![]() .
.
At the present time, we set t = t2. Then
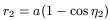
| (38) |
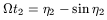
| (39) |
Then
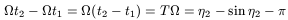
| (40) |
because
t2 - t1 = 14, if we adopt 1 Gyr as
time unity. We
know r2 = 650 (taking 1 kpc as distance unity). We also
know
![]() = - 125 (if we adopt 1 kpc/Gyr as unity for the
velocity; 1 km/s
= - 125 (if we adopt 1 kpc/Gyr as unity for the
velocity; 1 km/s ![]() 1 kpc/Gyr !)
1 kpc/Gyr !)

| (41) |
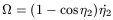
| (42) |
Eliminating
![]()
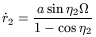
| (43) |
With (16) and (43)

| (44) |
and taking the value of ![]() given by (40)
given by (40)
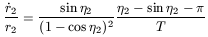
| (45) |
Defining,
![]() =
= ![]() -
- ![]()
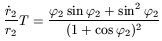
| (46) |
Taking the numerical values for r2, ![]() and T,
the solution of this equation, approximately, gives
and T,
the solution of this equation, approximately, gives
![]() = 1.59,
= 1.59,
![]() = 4.73. Hence (with (40)),
= 4.73. Hence (with (40)),
![]() = 0.18Gyr-1. Therefore
= 0.18Gyr-1. Therefore
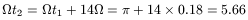
| (47) |
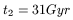
| (48) |
(Note that the time of the Big Bang is t1 = 17Gyr. We are not taking the Big Bang as the origin of time!). Then, with (38), we have:
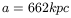
| (49) |
In our modest calculation, at the beginning both galaxies were 2a = 1324 kpc apart and they were at rest. Now they are 650 kpc apart (about half the initial distance) and they are approaching at 125 km/s.
With all these values, we deduce for the mass of the pair of galaxies
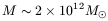
| (50) |
which is clearly much more than the visible mass of the pair of about
5 × 1011M![]() . Despite the long calculation, the
order of magnitude is just given by
M = V2r/G, where r and
V are the distance and velocity of M31.
. Despite the long calculation, the
order of magnitude is just given by
M = V2r/G, where r and
V are the distance and velocity of M31.
c) In the above argument we considered two mass points with mutual attraction, but the dark matter apparently encountered may be distributed in a single extended halo. If the force of gravity acting on the Galaxy were due to this Local Group super-halo, the equation to be integrated would be
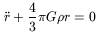
| (51) |
where ![]() is the density of the intergalactic medium, which, for
simplicity we assume to be constant. In this case the angular
velocity of the periodic motion would be
is the density of the intergalactic medium, which, for
simplicity we assume to be constant. In this case the angular
velocity of the periodic motion would be
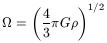
| (52) |
We can, as before, obtain detailed values of ![]() and the
initial distance between the new born Milky Way and the centre of the
Local Group, identified with the position of M31. In this case (r=a,
and the
initial distance between the new born Milky Way and the centre of the
Local Group, identified with the position of M31. In this case (r=a,
![]() = 0 at t = 0; the origin of time is now the
Big Bang,
approximately. Now, a is the maximum separation of the Milky Way,
instead of 2a, as in the previous case). We adopt
r = 650kpc,
= 0 at t = 0; the origin of time is now the
Big Bang,
approximately. Now, a is the maximum separation of the Milky Way,
instead of 2a, as in the previous case). We adopt
r = 650kpc,
![]() = - 125kpc/Mpc,
T = 14Gyr as before,
= - 125kpc/Mpc,
T = 14Gyr as before,
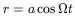
| (53) |
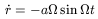
| (54) |
Dividing the formulae
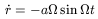
| (54) |
hence
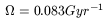
| (56) |
and
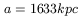
| (57) |
For the density of dark matter in the Local Group, we obtain
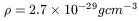
| (58) |
This value is much lower than the minimum value estimated by Kahn and
Woltjer (about
1.6 × 10-28gcm-3) and slightly higher than
the critical density to close the Universe (
![]() 10-29gcm-3). The common
halo hypothesis is not easy to reject.
10-29gcm-3). The common
halo hypothesis is not easy to reject.
d) The Local Group, rather than two main galaxies and several
satellites together with some minor members, should be considered as a
primordial inhomogeneity which has only recently collapsed to
form its present galactic members. Like any other inhomogeneity it has
evolved through the radiation dominated epoch with
![]() =
= ![]()
![]() /
/![]()
![]() R, decaying transverse velocities and
increasing radial
velocities in a moderate collapse. Then
inhomogeneities reached an acoustic epoch, which for masses typical of
the Local Group began at z = 105 approximately (see
later, Fig. 22). After the
Recombination epoch the Local Group pursued its process of collapse with
the relative density contrast increasing as R, where R is the
cosmological scale factor, the transverse
velocities decreasing as R-1 and - what is most
important for our
purposes- the radial velocities increasing as
R1/2. After that, the
collapse became non-linear and these variations with the cosmic scale
factor became complicated and faster. As
R, decaying transverse velocities and
increasing radial
velocities in a moderate collapse. Then
inhomogeneities reached an acoustic epoch, which for masses typical of
the Local Group began at z = 105 approximately (see
later, Fig. 22). After the
Recombination epoch the Local Group pursued its process of collapse with
the relative density contrast increasing as R, where R is the
cosmological scale factor, the transverse
velocities decreasing as R-1 and - what is most
important for our
purposes- the radial velocities increasing as
R1/2. After that, the
collapse became non-linear and these variations with the cosmic scale
factor became complicated and faster. As
![]()
![]() 1 we find
ourselves in the non-linear regimen, but we will consider a linear
evolution to find typical orders of magnitude. In this picture a naive
formula relating the
present velocity V0 of an inhomogeneity with present size
1 we find
ourselves in the non-linear regimen, but we will consider a linear
evolution to find typical orders of magnitude. In this picture a naive
formula relating the
present velocity V0 of an inhomogeneity with present size
![]() and actual relative density contrast is
(Battaner, 1996)
and actual relative density contrast is
(Battaner, 1996)
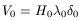
| (59) |
If the Milky Way and M31 were condensations within the Local Group,
V0 would be identified with the relative velocity
between these two
galaxies, with ![]() and
and ![]() being typical parameters
characterizing the size and the density contrast of the Local Group.
being typical parameters
characterizing the size and the density contrast of the Local Group.
This interpretation of the negative recession velocity of M31 is
fully compatible with the scenario of an approach between the two
galaxies within an expanding universe but somewhat in contrast with
present hierarchical models, in
which small structures form first, which will be accounted for later.
As the velocities, before
Recombination, do not reach high values
(Florido and Battaner, 1997)
we can start our calculations at Recombination. From the above formula,
taking
V0 ![]() 125km/s,
H0 = 60km/(sMpc) and
125km/s,
H0 = 60km/(sMpc) and
![]()
![]() 0.65Mpc, we obtain
0.65Mpc, we obtain
![]()
![]() 5.5. Then
5.5. Then
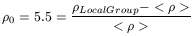
| (60) |
where < ![]() > is the average density in the Universe. Hence, for the
Local Group
> is the average density in the Universe. Hence, for the
Local Group
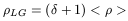
| (61) |
Let us adopt for
< ![]() > = 0.3 ×
10-29gcm-3, thus obtaining
> = 0.3 ×
10-29gcm-3, thus obtaining
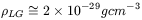
| (62) |
Let us compare the different results. Methods c) and d) give a similar
order of magnitude, about
2.7 × 10-29gcm-3. The mass
corresponding to this density depends on the volume. The density
surely decreases outwards. Suppose a moderate equivalent radius of 650
kpc; then the mass of the Local Group would be
4 × 1011M![]() , which is approximately the visible
mass. Or suppose an
equivalent radius of 1 Mpc. In this case, we obtain
1.5 × 1012M
, which is approximately the visible
mass. Or suppose an
equivalent radius of 1 Mpc. In this case, we obtain
1.5 × 1012M![]() , in reasonable agreement with method a).
, in reasonable agreement with method a).
Not only should the results be compared, but also the basic formulae when
the numerical coefficients close to unity are ignored. Essentially,
methods b) and c) use
M ![]() V2r/G, where V
is the
approaching velocity of M31 and r its distance. Of course, the more
detailed arguments presented provide a more precise result, but which
cannot greatly differ from this value (
2.3 × 1012M
V2r/G, where V
is the
approaching velocity of M31 and r its distance. Of course, the more
detailed arguments presented provide a more precise result, but which
cannot greatly differ from this value (
2.3 × 1012M![]() ). However, method d) is quite
different. The
order-of-magnitude lying behind the calculation is of the type
M
). However, method d) is quite
different. The
order-of-magnitude lying behind the calculation is of the type
M ![]()
![]() <
< ![]() >. In a critical Universe
<
>. In a critical Universe
< ![]() > = 3H02/8
> = 3H02/8![]() G. This method is not intrinsically related to
the other two. The orders of magnitude coincide because, curiously, V/r
is of the order of H0. In most pairs the orbital
period is of the
order of H0-1.
G. This method is not intrinsically related to
the other two. The orders of magnitude coincide because, curiously, V/r
is of the order of H0. In most pairs the orbital
period is of the
order of H0-1.
Summarizing, unless M31 and the Milky Way are like "ships passing in the night" (a possibility that cannot be totally disregarded), the Local Group seems to have 4 times more mass than we see as stellar light. But we don't know where this mass lies, whether in galactic dark matter halos or in a large common super halo. The difficulties encountered in the interpretation of the closest binary system are translated to the interpretation of other binary systems.