At large radii, gravity decreases as R-2. In contrast, magnetic fields evolve locally due to gas motions. As in the case of the Sun, at large enough radii, magnetic fields may become more important than gravity, or even dominant.
It is at present evident that 10
G fields exist in the inner
disks. It is increasingly evident that 1G fields exist in the
intergalactic medium, this point being addressed later. It is
therefore to be expected that in the region in between -the outer
disk- magnetic fields larger than 1G exist, even if they have
not been observed.
Then, at some radii the magnetic energy density should reach the order of magnitude of the rotation energy density
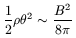
| (110) |
or, equivalently, the Alfven and the rotation speeds should have the same order of magnitude.
This equality of both energy densities will take place for a magnetic
field strength that depends on the gas density and on the rotation
velocity. Rotation velocities typically range from 50 to 200
kms-1. Typical values of n, the number density
of atoms, can be estimated as in our galaxy.
Burton (1976)
showed a plot in which
n 
0.2atoms cm-3 at 10 kpc and
n 0.01atoms cm-3 at
20 kpc. With an exponential decrease n should be about
2 × 10-3atoms cm-3 at 25 kpc.
Burton (1992)
gives similar values reaching
5 × 10-4atcm-3 at about 30 kpc. For other
galaxies it should be kept in mind that we measure the surface density
in atoms cm-2 and to obtain n, the flaring of
the layer must
be taken into account. For instance, for the Milky Way, the FWHM
thickness is about 300 pc at the Sun distance and at R 
20 kpc,
it is higher than 1 kpc
(Burton, 1992).
HI disks appear to have a
cut-off at about
1019atoms cm-2
(Haynes and Broeils, 1997).
Van Gorkom (1992)
found this cut-off at
4 × 1018atoms cm-2. For a thickness of
about 1 kpc, this corresponds to
n = 10-3atoms cm-3. This cut-off is
probably due to the ionization
of the intergalactic UV radiation, not to a cut-off in the hydrogen
itself. However, in our Galaxy, we observe number densities lower than
this. We should take
n = 0.3 - 3 × 10-4atoms cm-3 in the
region of more-or-less flat rotation curves.
The following table gives the magnetic field strength required to produce the same kinetic and magnetic energy densities.
Magnetic fields 0.1 this strength should already have a
measurable influence; a magnetic field of this strength would even be a
dominant effect. To interpret this table it is therefore to be
emphasized that with the strengths given, even gravitation would be
negligible.
 |
200 | 100 | 50 |
| n | |||
| 3 × 10-1 | 35 | 18 | 8 |
| 3 × 10-2 | 11 | 6 | 3 |
| 3 × 10-3 | 3 | 1 | 0.7 |
| 3 × 10-4 | 1 | 0.6 | 0.3 |
n in atoms cm-3, in kms-1, B in G.
For instance, in our galaxy, the magnetic field would be negligible at the Sun distance, important at 20 kpc and dominant at the rim.
Moreover, we can compare the gravitational attraction and the magnetic
force. For an order of
magnitude calculation let us adopt the point mass model,
GM/R2, where M is the
galactic mass (without dark matter) and
the magnetic force is, as we will see later, of the order of
(B2/R)(1/8
). For a galaxy like the Milky Way we obtain similar
values as before. A non-negligible magnetic field should be of the
order of 6G at R = 10 kpc, of 1G at R= 20 kpc and of
0.4G at R= 0.4 kpc.
For dwarf late-type galaxies, which are usually considered to need
higher dark matter ratios, the magnetic fields required are higher but
nevertheless worryingly large. Using the same estimation formula
GM/R2 B2/(8R) we have approximately
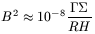
| (111) |
where 
is the visible M/L ratio in solar units, 
the
typical surface brightness in
L
pc-2, R the
radius in kpc
and H the scale height in kpc. For typical values, = 1,
= 0.3, R = 5, H = 0.5 (from
Swaters, 1999)
we obtain that a strength of
B 3.5 × 10-5G would produce a force
as important as
gravitation in the whole galaxy and that 1/10 this value
4 × 10-6G would be non-negligible. The
orders of magnitude
obtained by the equality of kinetic and magnetic energy are again
similar.
Following the analysis of
Vallée (1994),
the hypothesis of
magnetic-driven rotation curves is unsustainable. The
magnetic field strengths required in the model by
Battaner et al. (1992)
were too high, by at least a factor of 2, as compared to the
weaker magnetic field strengths observed.
Battaner et al. (1992)
indeed required high magnetic fields, of about 6 G at the
rim. However, after the publication of the study by
Vallée (1994),
Battaner and Florido (1995)
recalculated the strength required, by means of a two-dimension
model including escape and flaring, obtaining much lower values, of
the order of 1G. These values are not incompatible with
observations, for instance reviewed by
Vallée (1997),
in his
exhaustive analysis of cosmic magnetic fields at all scales, and in
particular in spiral galaxies. In this review, he collates a number of
measurements obtained by other authors and by himself. On the other
hand, there are not many measurements available for the outermost
region of the disk, as discussed later.
The figures in the above tables are worrying. It can be concluded that interpreting rotation curves, while ignoring the influence of magnetic fields may be completely unrealistic. It is therefore remarkable that a fact that may be so far-reaching concerning our cosmological beliefs has been object to such scarce attention.
The magnetic hypothesis takes this fact into consideration and tries to determine whether magnetic fields alone, without requiring any dark matter, and without modifying our physical laws, are able to explain the observed flat and fast rotation curves. The existence of dark matter cannot be completely excluded, but here we explore the extreme case with no DM at all.